一、神经元
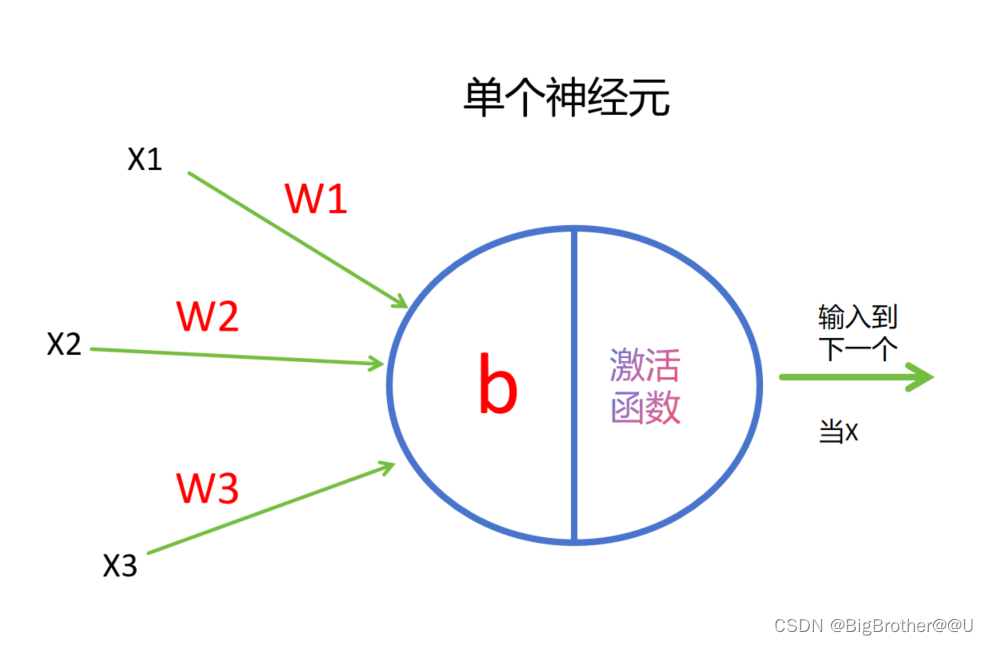
单个神经元结构其实可以认为是一个线性回归模型。例如下图中
该神经元输入为三个特征(x1,x2,x3),为了方便理解,大家可以认为每条线上都有一个权重和特征对应(w1,w2,w3)。当w1x1+w2x2+w3x3输入到神经元时,会加入一个偏置b,变为w1x1+w2x2+w3x3+b。我们可以把这个值当作f(x)。然后把f(x)送入激活函数比如sigmoid。最后得到的输出结果g(x) = sigmoid(f(x))。最后的g(x)作为xn会输入到下一个神经元。
记忆技巧tips:每个神经元,有多少个输入特征就有多少个边,边上就有多少个w,但有且只有一个b。
二、MLP
多个神经元按照一层层连接就组成了多层感知机(MLP)。如果是全连接网络((Fully Connected Netural Network,FCN),则每个神经元都会和它前层、后层所有神经元相连。
1、结构
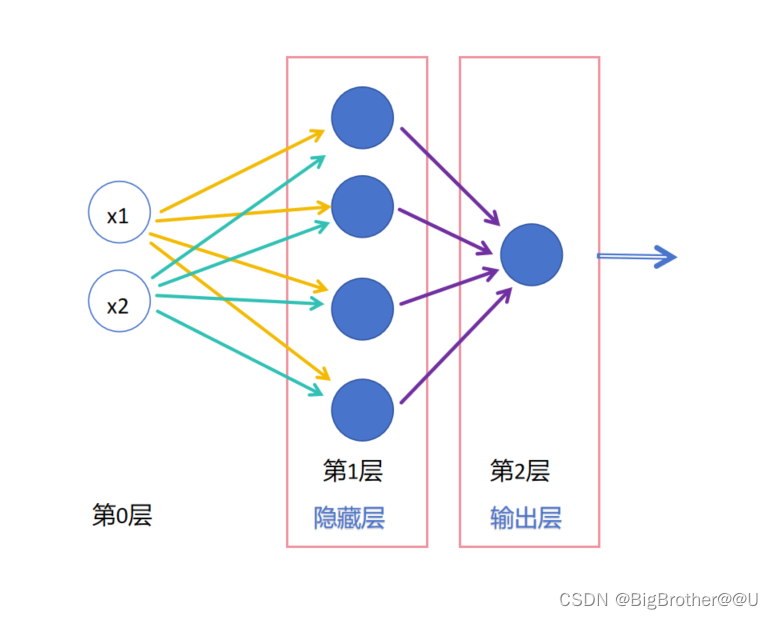
(1)图2,是两层全连接神经网络,明明是三层为什么叫两层神经网络?不是输入层(第0层),隐藏层,和输出层三层吗?在书中,只有隐藏层和输出层算层,输入层不算。可能设计输入的第0层的原因是:
可以理解为这一层主要是处理数据,也就是变换X,比如让数据归一化,one-hot编码什么的。
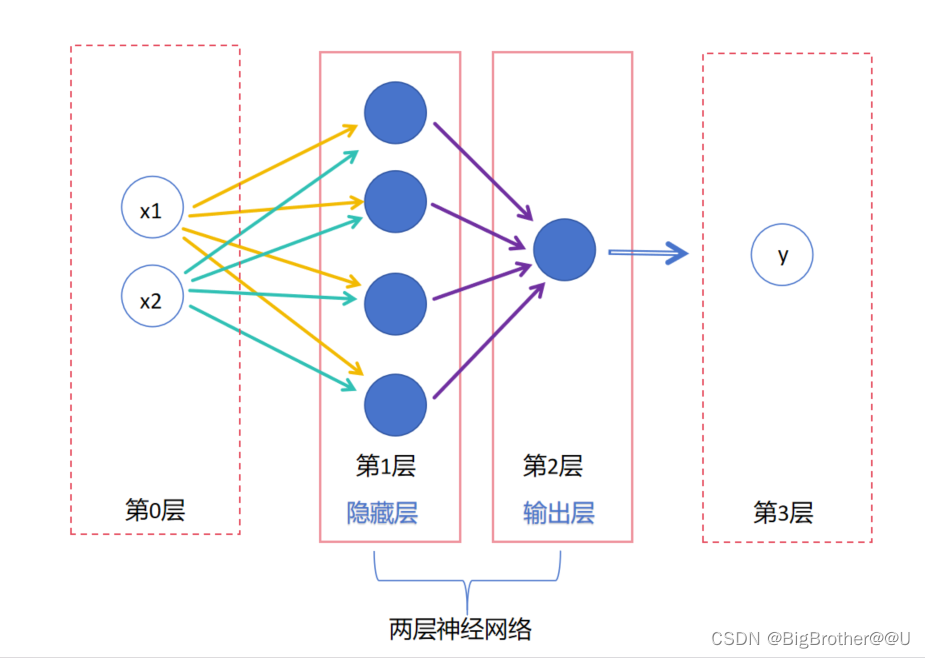
(2)上图是课本标准的多层神经网络,下面是为了理解绘制的不标准的示意图。其中画虚线的部分(第0层和第3层)不算神经网络的层,它只是最初的输入数据和最后的输出数据,是个名词相当于一个变量。我们看第1层(隐藏层)做了什么,它把第0层的输入x1和x2变为了输出(把黄色和绿色的线变为紫色)。第二层输出层把隐藏层的输出变为了整体的输出y(把紫色的线变为蓝色的线)。大家可以看出神经网络的层类似于动词相当于一个函数。下面的图是为了方便大家理解,如果绘制的话,还是要按照标准来。
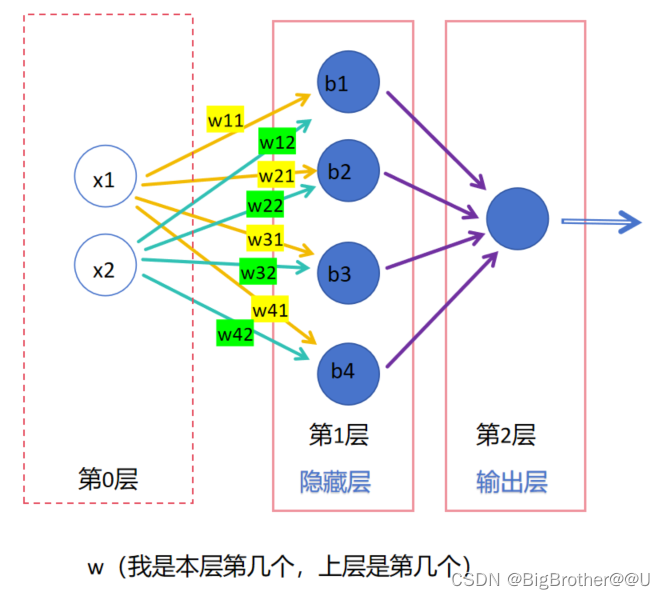
(3)每一层有n个神经元,为了区分不同神经元上的w,使用带两个数字的w(第一个数字是连接到本层第几个神经元,第二个数字是上层第几个神经元)来标识,比如图4,第1层的神经元中,w11标识本层第一个神经元和上层第一个神经元相连,w32表示本层第三个和上层第二个相连。b的话就是本层第几个神经元就是b几,比如b2表示本层第二个神经元上的偏置。
(4)我们再把视野扩大,刚刚说的是一层,如何标识不同层的w和b呢,比如第1层的w11和第2层的w11如何区别呢?一般我们会使用参数上标来标识是第几层的参数。如下图,比如w1表示第一层的w们。
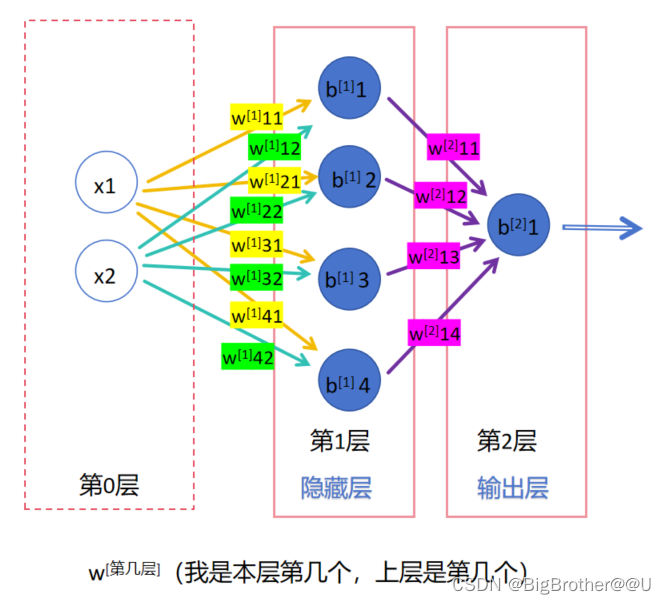
tips:其实在日常情况下使用上标标识第几层,使用下标来标识参数关系的,比如w[1]11 这是标准写法,而不是w[1]11
2、分类 or 回归
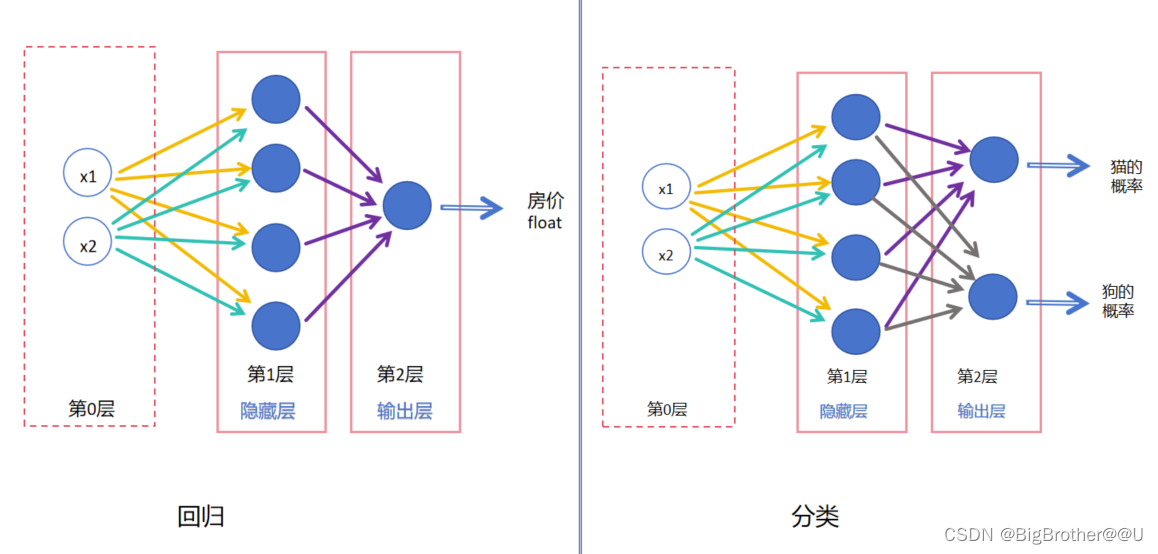
回归:最后的输出层只有一个神经元,一般预测结果是float值,比如根据x1房子面积,x2房子年龄,预测最后的房屋价格。
分类:几个分类,最后输出层就有几个神经元。比如猫狗二分类,最后输出层是两个神经元,如果最后是十分类,那么最后一层就是十个神经元。
3、前向传播
(1)从神经网络前面把数据从输入到输出的过程为前向传播。比如图2,数据x1,x2输入到隐藏层1,然后计算后输入到输出层,最后输出结果。
类似线性模型,即输入x,使用参数w,b计算wx+b的过程。
(2)平时都是按照一个批次进行矩阵计算的,下面是批量为3时输入到图5第一层神经网络的情况。
输入的数据为(批量*特征个数)形状的矩阵,
隐藏层的参数W为(特征个数*本层神经元个数)形状的矩阵,
b为(1*神经元个数)形状的向量。

4、反向传播
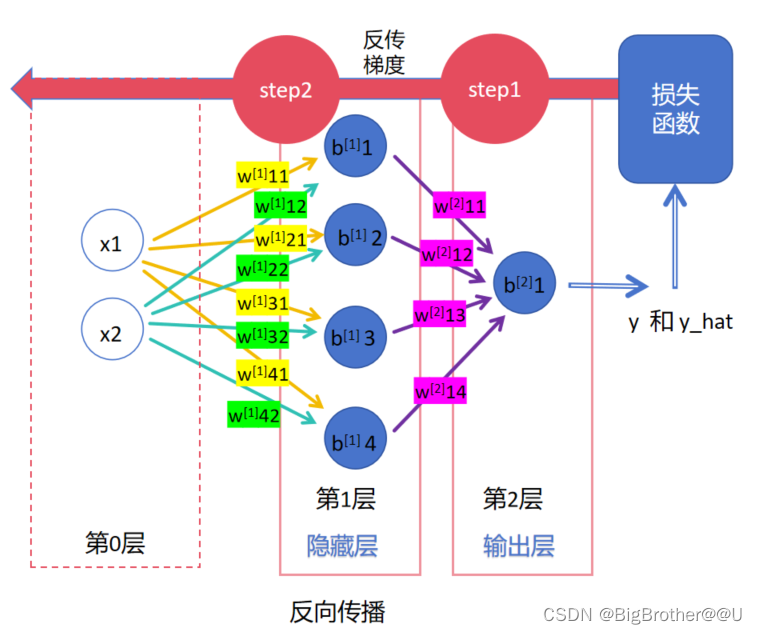
反向传播的是梯度,梯度下降是为了优化每一层的参数。
step1:
神经网络最后的输出结果为y_hat,训练数据中的标签为y,使用损失函数计算两者的误差。此时,第2层的w、b参数可以使用梯度下降直接更新了,因为本层的w,b直接组成了loss函数即 : loss(w[2]11O1+w[2]12O2+w[2]13O3+w[2]14O4+b[2]1-y),比如该值为loss1,loss1对w[2]11求偏导,然后乘以学习率得出更新的值,w[2]11减去更新的值即为更新后的w[2]11。
step2:
把第2层的梯度传到第1层,根据链式法则,第1层的参数可以进行更新。
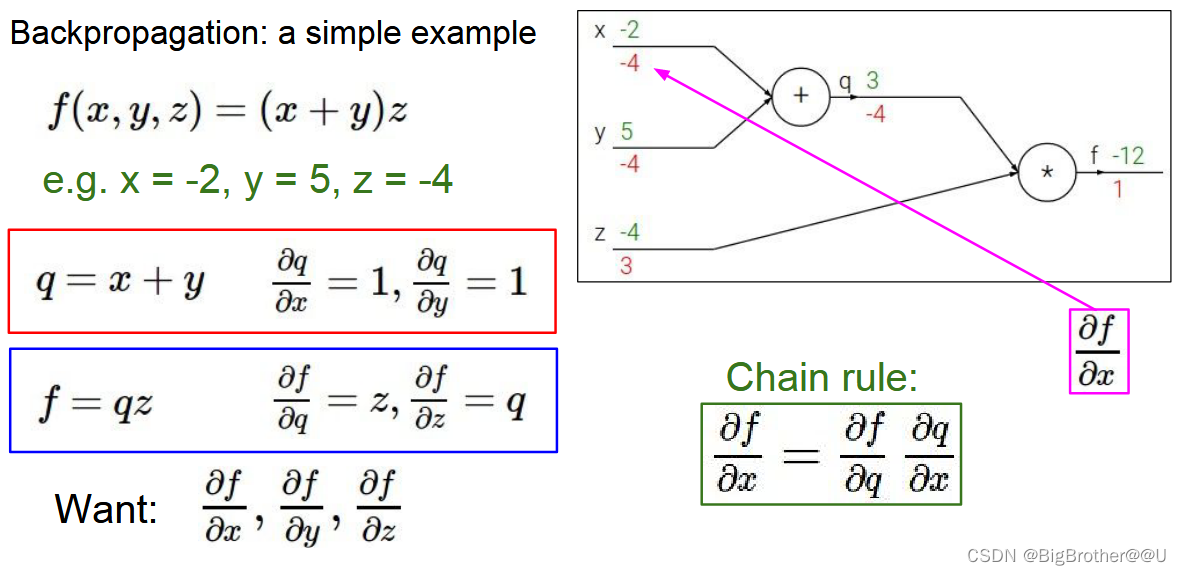
下面我们举个例子详细说一下反向传播梯度。
下图中x,y,z都可以看作是w参数,f函数看为损失函数。绿色为特征x,y,z现在的值,红色为对应的导数(梯度)。比如求x的梯度,根据链式法则,先f对q求导,然后求q对x的导数,结果为-4*1,1是本地计算的梯度,-4是反向传过来的梯度。