在程序开发中,算法是解决问题的核心。本篇博客将详细讲解一种高效的查找算法——二分查找,并通过Java代码示例帮助你理解其实现和应用。
如果你觉得这篇文章对你有帮助,不要忘记点赞、收藏和关注我,这将是对我最大的支持和鼓励!
什么是算法?
算法是解决问题的一系列步骤或规则。它们是计算机程序的核心,决定了程序的性能和效率。一个好的算法可以极大地提高程序的运行速度和资源利用率。
大O表示法
大O表示法用于描述算法的效率,特别是它在数据规模增长时的表现。常见的大O表示法包括:
- O(1):常数时间,不论数据规模多大,执行时间都不变。
- O(log n):对数时间,常见于二分查找。
- O(n):线性时间,算法的执行时间与数据规模成正比。
- O(n log n):线性对数时间,常见于快速排序、归并排序等。
- O(n^2):平方时间,常见于简单排序算法,如冒泡排序。
- O(2^n):指数时间,常见于解决复杂问题的递归算法。
二分查找简介
二分查找是一种用于在有序数组中查找特定元素的高效算法。其基本思想是通过逐步缩小查找范围,将查找时间复杂度降低到 O(log n)。相比于线性查找的 O(n),二分查找的效率要高得多。
二分查找步骤
- 找到数组的中间元素。
- 如果中间元素正好是目标元素,查找成功。
- 如果目标元素比中间元素小,则在左半部分继续查找。
- 如果目标元素比中间元素大,则在右半部分继续查找。
- 重复上述步骤,直到找到目标元素或范围缩小为零。
二分查找图解
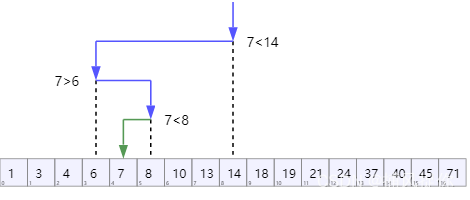
Java实现
下面是一个简单的Java代码实现:
public class BinarySearch {
public static int binarySearch(int[] array, int target) {
int low = 0;
int high = array.length - 1;
while (low <= high) {
int mid = (low + high) / 2;
int guess = array[mid];
if (guess == target) {
return mid;
} else if (guess > target) {
high = mid - 1;
} else {
low = mid + 1;
}
}
return -1; // 表示未找到
}
public static void main(String[] args) {
int[] array = {1, 3, 5, 7, 9};
int target = 7;
int result = binarySearch(array, target);
System.out.println("元素 " + target + " 的索引为: " + result);
}
}
代码解释
binarySearch方法接受一个有序数组和一个目标值作为输入。- 通过初始化
low和high指针,逐步缩小查找范围。 - 计算中间位置
mid并检查其值是否等于目标值。 - 根据目标值与中间值的比较结果,调整
low和high指针。 - 循环直到找到目标值或范围缩小为零。
算法分析
- 时间复杂度:二分查找的时间复杂度为 O(log n),因为每次查找都会将查找范围减半。
- 空间复杂度:二分查找的空间复杂度为 O(1),因为它只使用了常数的额外空间。
示例运行结果
运行上述代码,你将看到以下输出:
元素 7 的索引为: 3
练习题
- 修改
binarySearch方法,使其能处理包含重复元素的数组,并返回第一个匹配的元素。 - 实现一个线性查找算法,并比较它与二分查找的性能。
总结
通过本文的学习,我们了解了二分查找的基本概念、实现步骤和Java代码示例。二分查找是一种高效的查找算法,适用于大多数有序数据集的查找问题。
如果你觉得这篇文章对你有帮助,请点赞、收藏,并关注我的CSDN博客。我会持续分享更多高质量的算法和编程知识。
感谢你的阅读和支持!如果有任何问题或建议,欢迎在评论区留言,我会尽快回复。
希望这篇博客对你有帮助。如果有任何问题或需要进一步的解释,请告诉我!