1、绪论
在密码学体系中,对称加密、非对称加密、单向散列函数、消息认证码、数字签名和伪随机数生成器被统称为密码学家的工具箱。其中,对称加密和非对称加密主要是用来保证机密性;单向散列函数用来保证消息的完整性;消息认证码的功能主要是认证;数字签名保证消息的不可抵赖性。
在零知识证明中,涉及较多的加密方案是非对称密码体制( 又称为公钥密码体制) 。非对称密码体制使用公钥加密消息,使用私钥来解密。使用非对称密码体制可增强系统的安全性。
2、发展史
密码学的发展大致可以分为 3 个阶段: 1949 年之前的古典密码学阶段; 1949 年至 1975 年密码学成为科学的分支; 1976 年以后对称密钥密码算法得到进一步发展,产生了密码学的新方向—公钥密码学。1976 年,W.Diffie 和 M.Hellman 在发表的文章“密码学的新方向”中首次公开提出了公钥密码( Public-key Cryptography) 的概念。公钥密码的提出实现了加密密钥和解密密钥之间的独立,解决了对称密码体制中通信双方必须共享密钥的问题,在密码学界具有划时代的意义。
3、对称加密
对称加密整个加密过程中只使用一个密钥。所谓对称其实就是使用一把密钥加密,使用同一把密钥解密。
对称加密的主要有优点就是算法公开、计算量小、加密速度快、加密效率高;但是它也存在强大的缺点,一旦密钥泄露,别人可以获取到密钥,这样也能对密文进行解密。下面是对称加密的操作过程:
设用户 A A A把信息 M M M发送给用户 B B B, A A A和 B B B不希望 M M M传递的过程中被第三方看到,可以采取的方法是, A A A先对 M M M进行处理。然后发送处理后的结果。对 M M M处理实际上是进行某种数学运算,运算结果我们用 E ( M ) E(M) E(M)表示, B B B收到 E ( M ) E(M) E(M)后,会按事前与 A A A约定好的方法从 E ( M ) E(M) E(M)中把M还原出来,结果我们用 D ( E ( M ) ) = M D(E(M))=M D(E(M))=M表示。第三方即使截获到 E ( M ) E(M) E(M),因为不知道还原方法,从而无法看到 M M M, A A A与 B B B也就达到了秘密通信的目的。
前面过程中的 E E E我们称之为加密算法, D D D称之为解密算法,二元组 ( E , D ) (E,D) (E,D)表示一个特定的加/解密算法,这个二元组是 A A A与 B B B提前约定好的,当然二元组 ( E , D ) (E,D) (E,D)只有 A A A和 B B B知道,其他第三方是不知道的。
当 A A A与另一个网络用户 C C C安全通信时,就不能再用二元组 ( E , D ) (E,D) (E,D)了,需要改换成另一个加/解密二元组 ( E ′ , D ′ ) (E',D') (E′,D′)。由此看来, A A A与多个用户安全通信,就需要有多个加解密二元组。
开发多个加解密二元组不是一件容易的事,可以在加/解密二元组
(
E
,
D
)
(E,D)
(E,D)基础上增加一个参数,
A
A
A与
B
B
B之外的其他用户通信只要选择不同的参数值就可以了。具体来说,
A
A
A和
B
B
B之间的通信选择参数
s
1
s_1
s1,
A
A
A与
C
C
C之间的通信选择
s
2
s_2
s2
,即使大家都采用二元组(E,D),也能做到安全通信,这就避免了为不同用户对开发不同的二元组了,这里的参数
s
1
s_1
s1和
s
2
s_2
s2就是所谓的密码或者秘钥,
s
1
s_1
s1
由
A
A
A和
B
B
B秘密保管,
s
2
s_2
s2由
A
A
A和
C
C
C秘密保管。
所有用户采用同一个加解密二元组 ( E , D ) (E,D) (E,D),只是不同用户对采用不同密钥的加解密体制,因此被称为对称加密体制。下面是对称密码体制的典型流程:
已知二元组 ( E , D ) (E,D) (E,D),用户 A A A与 B B B之间的共享密钥是 p p p, A A A把信息 M M M安全发送给 B B B
- A A A利用 p p p和加密算法 E E E对信息 M M M处理,结果记作 E p ( M ) E_p(M) Ep(M)
- A A A把 E p ( M ) E_p(M) Ep(M)发送给 B B B;
- B收到 E p ( M ) E_p(M) Ep(M),并对 E p ( M ) E_p(M) Ep(M)用秘钥 p p p和解密算法 D D D处理,结果记作 D p ( E p ( M ) ) = M D_p(E_p(M))=M Dp(Ep(M))=M。
常用的对称加密算法有 DES、3DES、AES、TDEA、Blowfish、RC2、RC4 和 RC5 等。
4、AES加密算法
AES 加密算法是一种分组密码体制,将明文按照固定大小进行分组,然后对每一分组进行加密。在加密过程中,AES 算法采用了多轮加密的方式,算法主要可以分为秘钥扩展、字节替换、行移位、列混合和轮秘钥加这5个步骤。
-
秘钥扩展(KeyExpansions:在 AES 加密算法中,明文被分成若干个固定长度的块。常见的分组长度为 128 比特,即每个明文块包含 16 个字节。如果明文长度不是 16 的整数倍,则需要对原始秘钥进行填充。实际上密钥长度可以是 128 比特、192 比特或 256 比特。对于不同长度的密钥,需要经过不同的轮数来扩展密钥。具体而言,128 比特密钥需要经过 10 轮扩展,192 比特密钥需要经过 12 轮扩展,256 比特密钥需要经过14轮扩展。
-
字节替换(SubBytes):字节替换是通 过 S-BOX对字节元素进行变换,S-BOX由有限域 G F 2 8 GF_{2^8} GF28上的乘法求逆运算和仿射变换运算而来,通过查表的方式即可直接得到变换前后的字节元素,替换后字节元素至少有两位发生变换,能充分打乱原来的字节元素。也可以认为S-BOX是一张固定大小的表格,由 256 个字节组成。通过输入表格中的某一字节,就可以得到表格中对应的输出字节。
-
行移位(ShiftRows):将数据矩阵的每一行循环移位一定长度。
-
列混合(MixColumns):将数据矩阵乘以一个固定的矩阵,增加混淆程度。
-
轮秘钥加(AddRoundKey):将数据矩阵与秘钥矩阵进行异或操作。
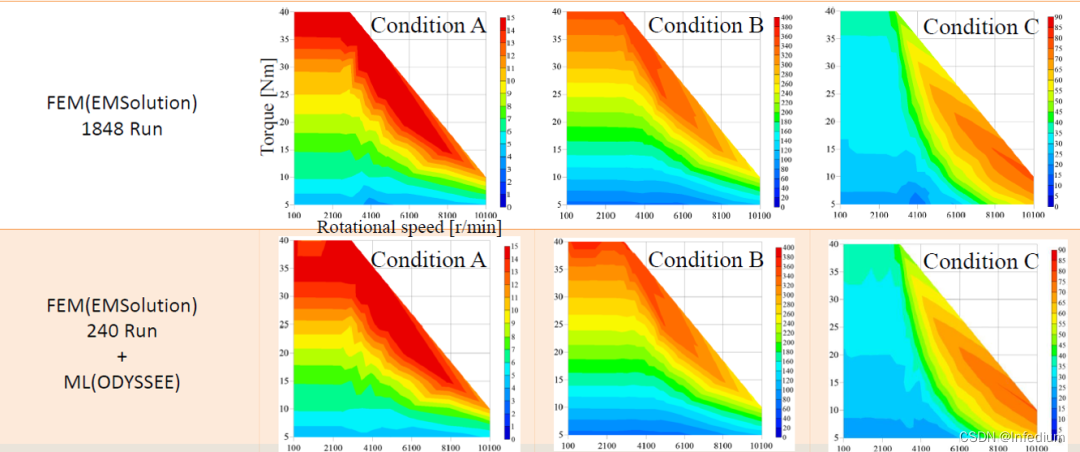
下图为AES加密算法流程。
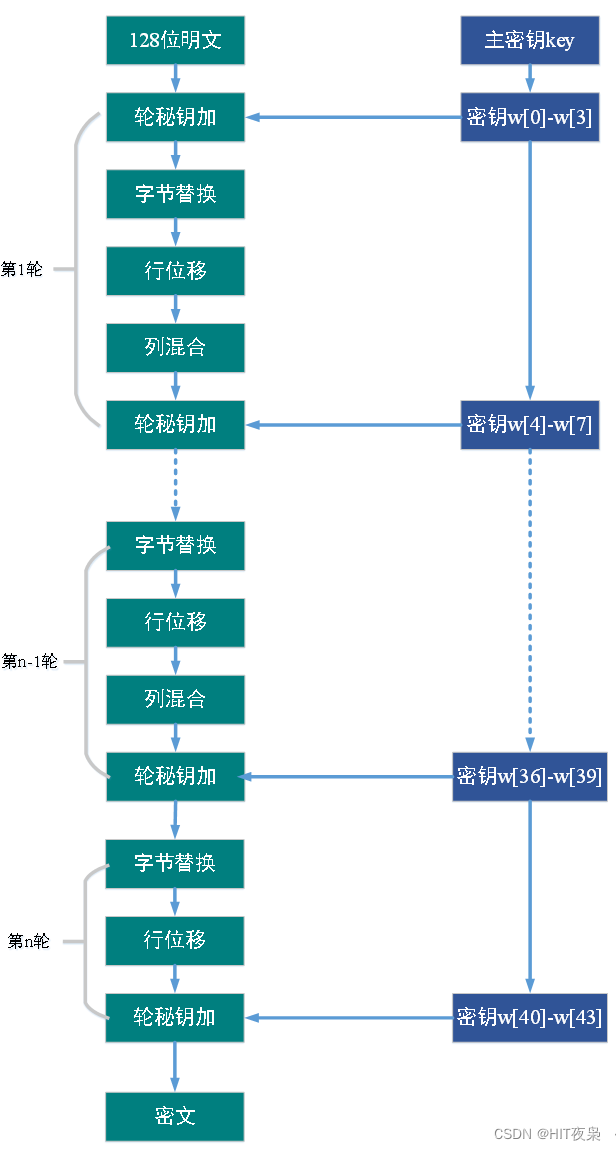
AES是用来替代DES的新一代加密标准,具有128bit的分组长度,支持128、192和256比特的密钥长度,它是目前最流行的对称加密算法之一。
5、非对称加密
非对称加密又称为公钥密码,该技术是针对私钥密码体制(对称加密算法)的缺陷被提出来的,非对称加密会产生两把密钥,分别为公钥(Public Key)和私钥(Private Key),其中一把密钥用于加密,另一把密钥用于解密。非对称加密的特征是算法复杂、安全性依赖于算法与密钥。但是由于其算法复杂,而使得加密解密速度没有对称加密解密的速度快。
在使用非对称加密时,任何人都可以使用预期接收者的公钥对消息进行加密,但该加密消息只能使用接收者的私钥解密。
已知公钥密码算法二元组 ( E , D ) (E,D) (E,D),用户 A A A把信息 M M M安全发给用户 B B B,下面是非对称密码体制的典型流程:
- 利用 ( E , D ) (E,D) (E,D)为用户 A A A产生公钥 p a p_a pa,私钥 s a s_a sa,为用户 B B B产生公钥 p b p_b pb
,私钥 s b s_b sb;
-
A A A用 B B B的公钥 p b p_b pb和加密算法 E E E对消息 M M M进行处理,处理结果记为 E p b ( M ) E_{p_b}(M) Epb(M)
-
A A A把 E p b ( M ) E_{p_b}(M) Epb(M)发送给用户 B B B;
-
B B B使用解密算法 D D D对收到的 E p b ( M ) E_{p_b}(M) Epb(M)进行处理,结果为 D s b ( E p b ( M ) ) = M D{s_b}(E_{p_b}(M))=M Dsb(Epb(M))=M
非对称加密中对任何用户,不能从公钥导出其私钥;用谁的公钥加密,只能用谁的私钥解密。
常用的非对称加密算发有 RSA、Elgamal、背包算法、Rabin、D-H、ECC(椭圆曲线加密算法)等。
5、基于大整数素因子分解困难的RSA加密算法
RSA 算法是一种迄今为止理论上比较成熟和完善的公钥密码体制,是非对称密码体制的典型代表。在网络、信息安全等许多方面都使用 RSA 算法,特别是 RSA 算法典型应用在通信中的数字签名,可实现对手的身份、不可抵赖性验证。在身份认证、信息安全、电子商务中有着广泛的应用前景。
RSA加密算法相关的数学知识包括:
- 欧几里得算法:即 gcd ( a , b ) \gcd(a,b) gcd(a,b),值为 a a a和 b b b的最大公约数;
- 互质:即 gcd ( a , b ) = 1 \gcd(a,b) = 1 gcd(a,b)=1 <=> a a a和 b b b互质( a a a和 b b b没有1以外的公因子);
- 欧拉函数:即 φ ( n ) \varphi (n) φ(n),值为所有不大于 n n n且和 n n n互质的自然数的个数
- a ≡ b m o d P a ≡ b \mod P a≡bmodP 表示 a a a和 b b b在模 P P P下同余,即 a a a除以 P P P得到的余数和 b b b除以 P P P得到的余数相同;
- 欧拉费马定理:如果 gcd ( a , n ) = 1 \gcd(a,n) = 1 gcd(a,n)=1,则 a φ ( n ) ≡ 1 m o d n a^{ φ(n)} ≡ 1 \mod n aφ(n)≡1modn.
RSA 算法由密钥生成、加密和解密 3个部分组成,具体如下。
密钥生成:
- 产生两个大素数 p p p 和 q q q ;
- 计算 n = p × q n = p × q n=p×q,计算欧拉函数 φ ( n ) = ( p − 1 ) ( q − 1 ) φ(n) =(p - 1)(q - 1) φ(n)=(p−1)(q−1);
- 选择整数 e e e,使其满足条件: 1 < e < φ ( n ) 1 < e < φ(n) 1<e<φ(n),且 gcd ( e , φ ( n ) ) = 1 \gcd(e,φ(n)) = 1 gcd(e,φ(n))=1;
- 计算 e e e 的逆元 d d d: d ⋅ e ≡ 1 m o d φ ( n ) d\cdot e ≡ 1 \mod φ(n) d⋅e≡1modφ(n)(注:由于 gcd ( e , φ ( n ) ) = 1 \gcd(e,φ(n)) = 1 gcd(e,φ(n))=1,则 d d d一定存在);
- 取序对 ( e , n ) (e,n) (e,n) 为公钥,可公开; ( d , n ) (d,n) (d,n)为私钥,对外保密。
加密:
- 将要发送的字符串分割为长度为 m < n m < n m<n 的分组,然后对分组 m i m_i mi执行加密运算,得到密文 c i : c i ≡ ( m i ) e m o d n c_i :c_i ≡(m_i)^e \mod n ci:ci≡(mi)emodn
解密:
- 收到密文 c i c_i ci后,接收者使用自己的私钥执行解密运算,得到明文 m i : m i ≡ ( c i ) d m o d n m_i :m_i ≡(c_i)^d \mod n mi:mi≡(ci)dmodn
如果有任何人想要破解私钥 d d d,那就必须算出 φ ( n ) φ(n) φ(n)(因为 d d d满足 d ⋅ e m o d φ ( n ) ≡ 1 d\cdot e \mod φ(n)≡1 d⋅emodφ(n)≡1,且 e e e和 n n n是公开的),根据欧拉公式, φ ( n ) = ( p − 1 ) x ( q − 1 ) φ(n) = (p - 1) x (q - 1) φ(n)=(p−1)x(q−1),而通过一个大整数 n n n分解得到它的两素因子 p p p和 q q q是极端困难的,所以RSA的安全性也取决于这个大整数 n n n的位数.
6、基于离散对数难解性的ECC加密算法
椭圆曲线加密算法(ECC)是基于椭圆曲线数学的一种非对称密码算法,是建立在基于离散对数问题上的密码体制。随着分解大整数方法的进步以及各方面的完善,RSA 算法渐渐不能满足现状,ECC算法的需求性逐渐增大。ECC 以其明显的“短密钥”优势得到了广泛应用,并逐渐被确定为许多编码方式的数字签名标准。然而,ECC算法复杂度高,实现相对复杂,需要复杂的椭圆曲线运算。
ECC加密算法相关的椭圆曲线知识:
- 韦尔斯特拉方程 : E : y 2 + a x y + b y = x 3 + c x 2 + d x + e E:y^2+axy+by=x^3+cx^2+dx+e E:y2+axy+by=x3+cx2+dx+e。密码学中,常采用的椭圆曲线为: E : y 2 = x 3 + a x + b E:y^2=x^3+ax+b E:y2=x3+ax+b,并要求 4 a 3 + 27 b 2 ≠ 0 4a^3 + 27b^2≠0 4a3+27b2=0,且椭圆曲线有且只有一个无穷远点 O O O ;
- Hasse定理:如果 E E E是有限域 G F p GF_p GFp上的椭圆曲线, ( x , y ) (x,y) (x,y)是 E E E上的点,其中 x , y ∈ G F p x,y\in GF_p x,y∈GFp,曲线上的每个点都是非奇异的;
- 椭圆曲线上的点集合对于加法规则构成一个Abel群:
O
+
O
=
O
O+O=O
O+O=O;
椭圆上的点 P P P, P + O = P P+O=P P+O=P; P P P的逆元是 − P -P −P,且 P + ( − P ) = O P+(-P)=O P+(−P)=O;加法满足交换律和结合律; - 椭圆曲线加法;椭圆曲线上的点
P
(
x
1
,
y
1
)
P(x_1 ,y_1 )
P(x1,y1),
Q
(
x
2
,
y
2
)
Q(x_2 ,y_2 )
Q(x2,y2)的和
R
(
x
3
,
y
3
)
R(x_3 ,y_3 )
R(x3,y3)有如下关系:
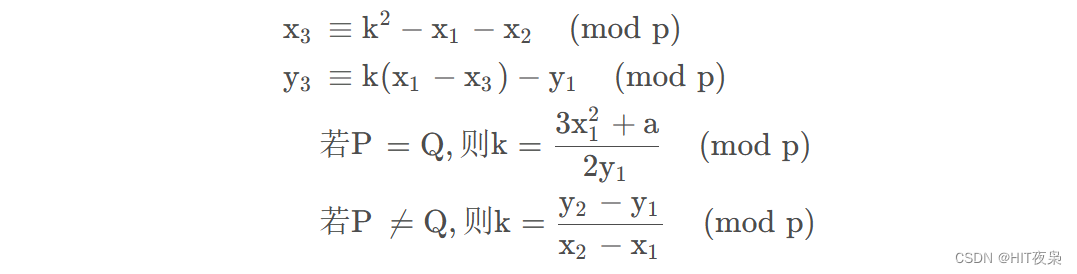
- 如果椭圆曲线上一点
P
P
P,存在最小的正整数
n
n
n使得数乘
n
P
=
O
n P = O
nP=O
,则将 n n n称为 P P P的阶,若 n n n不存在,则 P P P是无限阶的.
ECC算法也是由密钥生成、加密和解密 3个部分组成,具体如下。
密钥生成:
- 选择一个椭圆曲线 E E E,构造一个椭圆群 E p ( a , b ) E_p(a,b) Ep(a,b)。。
- 在椭圆群中挑选生成元点 G = ( x 0 , y 0 ) G=(x_0,y_0) G=(x0,y0),需满足 n G = O nG=O nG=O的最小的 n n n是一个非常大的素数。
- 选择一个小于 n n n的整数 n B n_B nB作为私钥,然后利用 P B = n B G P_B=n_BG PB=nBG算出 P B P_B PB。
- 公钥为 ( E , n , G , P B ) (E,n,G,P_B) (E,n,G,PB),私钥为 n B n_B nB。
加密:
- 用户A将明文消息编码成一个数 m < p m<p m<p,并在椭圆群 E p ( a , b ) E_p(a,b) Ep(a,b)中任选一点 P t = ( x t , y t ) P_t=(x_t,y_t) Pt=(xt,yt);
- 在区间 [ 1 , n − 1 ] [1,n-1] [1,n−1]内,用户A选取一个随机数 k k k,计算 P 1 : P 1 = ( x 1 , y 1 ) = k G P_1:P_1=(x_1,y_1)=kG P1:P1=(x1,y1)=kG;
- 依据接收方 B B B的公钥 P B P_B PB,用户 A A A计算点 P 2 : P 2 = ( x 2 , y 2 ) = k P B P_2:P_2=(x_2,y_2)=kP_B P2:P2=(x2,y2)=kPB;
- 用户 A A A计算密文 C = m x t + y t C=mx_t+y_t C=mxt+yt;
- A A A传送加密数据 C m = { k G , P t + k P B , C } C_m=\{kG,P_t+kP_B,C\} Cm={kG,Pt+kPB,C}给接收方 B B B.
解密:
- 接收方 B B B收到 C m C_m Cm;
- 接收方
B
B
B使用私钥
n
B
n_B
nB做运算:
P
t
+
k
P
B
−
n
B
(
k
G
)
=
P
t
+
k
(
n
B
G
)
−
n
B
(
k
G
)
=
P
t
P_t+kP_B-n_B(kG)=P_t+k(n_BG)-n_B(kG)=P_t
Pt+kPB−nB(kG)=Pt+k(nBG)−nB(kG)=Pt;
*接收方 B B B计算 m = ( C − y t ) / x t m=(C-y_t)/x_t m=(C−yt)/xt,得明文 m m m。
密码学中,描述一条 F p F_p Fp上的椭圆曲线,常用到六个参量: T = ( p , a , b , G , n , h ) T=(p,a,b,G,n,h) T=(p,a,b,G,n,h)。 ( p , a , b ) (p ,a ,b) (p,a,b)用来确定一条椭圆曲线, G G G为基点, n n n为点 G G G的阶, h h h 是椭圆曲线上所有点的个数 m m m与 n n n相除的整数部分.
这几个参量取值的选择,直接影响了加密的安全性。参量值一般要求满足以下几个条件:
- 1、 p p p当然越大越安全,但越大,计算速度会变慢,200位左右可以满足一般安全要求;
- 2、 p ≠ n × h p≠n×h p=n×h;
- 3、 p t ≠ 1 m o d n , 1 ≤ t < 20 pt≠1 \mod n,1≤t<20 pt=1modn,1≤t<20;
- 4、 n n n为素数;
- 5、 h ≤ 4 h≤4 h≤4。
7、比特币中的非对称加密ECC
比特币系统选用的secp256k1中,ECC参数为:
p
=
0
x
F
F
F
F
F
F
F
F
F
F
F
F
F
F
F
F
F
F
F
F
F
F
F
F
F
F
F
F
F
F
F
F
F
F
F
F
F
F
F
F
F
F
F
F
F
F
F
F
F
F
F
F
F
F
F
E
F
F
F
F
F
C
2
F
p=0xFFFFFFFF FFFFFFFF FFFFFFFF FFFFFFFF FFFFFFFF FFFFFFFF FFFFFFFE FFFFFC2F
p=0xFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFEFFFFFC2F
=
2
256
−
2
32
−
2
9
−
2
8
−
2
7
−
2
6
−
2
4
−
1
= 2^{256} − 2^{32} − 2^9 − 2^8 − 2^7 − 2^6 − 2^4 − 1
=2256−232−29−28−27−26−24−1,
a = 0 a = 0 a=0,
b = 7 b = 7 b=7,
G = ( 0 x 79 B E 667 E F 9 D C B B A C 55 A 06295 C E 870 B 07029 B F C D B 2 D C E 28 D 959 F 2815 B 16 F 81798 , 0 x 483 a d a 7726 a 3 c 4655 d a 4 f b f c 0 e 1108 a 8 f d 17 b 448 a 68554199 c 47 d 08 f f b 10 d 4 b 8 ) G=(0x79BE667EF9DCBBAC55A06295CE870B07029BFCDB2DCE28D959F2815B16F81798, 0x483ada7726a3c4655da4fbfc0e1108a8fd17b448a68554199c47d08ffb10d4b8) G=(0x79BE667EF9DCBBAC55A06295CE870B07029BFCDB2DCE28D959F2815B16F81798,0x483ada7726a3c4655da4fbfc0e1108a8fd17b448a68554199c47d08ffb10d4b8),
n = 0 x F F F F F F F F F F F F F F F F F F F F F F F F F F F F F F F E B A A E D C E 6 A F 48 A 03 B B F D 25 E 8 C D 0364141 n = 0xFFFFFFFF FFFFFFFF FFFFFFFF FFFFFFFE BAAEDCE6 AF48A03B BFD25E8C D0364141 n=0xFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFEBAAEDCE6AF48A03BBFD25E8CD0364141,
h = 01 h = 01 h=01.