一.指针和二维数组

1.如a是一个二维数组，则数组中的第i行可以看作是一个一维数组，这个一维数组的数组名是a[i]。

2.a[i]代表二维数组中第i行的首个元素的地址，即a[i][0]的地址。

二.进一步思考

二维数组可以看作是数组的数组，本质还是一维数组。所以我们可以把二维数组的一行看作是一个数组元素，此时二维数组就会变成一个一维数组。如下图所示

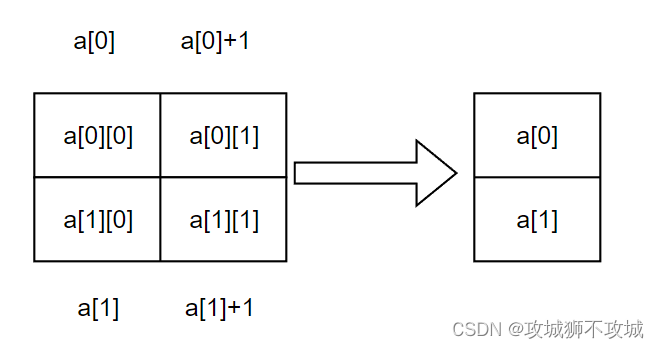
此时，二维数组a[2][2]变成了只有俩个元素a[0]和a[1]的一维数组。因为在一维数组中p=&a[0]可以简写成p=a；

所以由此得出：

数组名a就是一维数组元素a[0]的地址，即二维数组a中第0行的地址。a+1则是二维数组a中第1行的地址。所以a+i则是二维数组a中第i行的地址。

结论：

a+i与a[i]的地址相同的。

这里需要注意的是：*(a+i)+j才是a[i][j]的地址。并不是(a+i)+j是a[i][j]的地址。

因为a+i表示的是二维数组中第i行的地址，而不是第i行首个元素的地址，此时a+i表示的是整个第i行数组，*a+i表示的才是第i行数组中首个元素的地址。也就是说虽然a和*a的值相同，但是表示的意义不同。

举例验证：

#include <stdio.h>

int main(void)
{
    int a[2][2]={0,1,2,3};
    int i = 0;
    int j = 0;

    for(i=0;i<2;i++){
        for(j=0;j<2;j++){
            printf("a[%d][%d] addr is %p,value is %d\n",i,j,a[i]+j,*(a[i]+j));
        }
    }
    printf("**********************************\n");
    for(i=0;i<2;i++){
        for(j=0;j<2;j++){
            printf("a[%d][%d] addr is %p,value is %d\n",i,j,*(a+i)+j,*(*(a+i)+j));
        }
    }

    printf("%p\n",*a);
    printf("%p\n",*a+1);
    printf("%p\n",a);
    printf("%p\n",a+1);


    return 0;
 
}

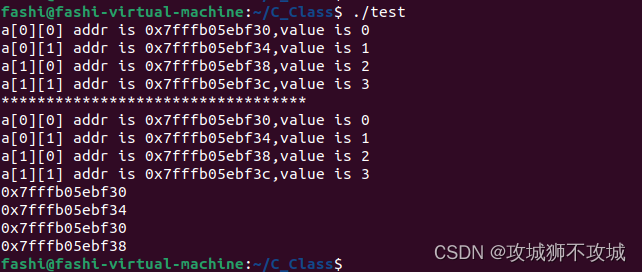
运行结果:

三.视频教程

62.指针和二维数组（2）_哔哩哔哩_bilibili