2.1 逻辑代数(简单逻辑的运算)
2.2 逻辑函数的卡诺图(从图论的角度)化简法
2.3 硬件描述语言Verilog HDL基础(研究生阶段才用得到)
要求:
1、熟悉逻辑代数常用基本定律、恒等式和规则。
2、掌握逻辑代数的变换和卡诺图化简法;
2.1.1 逻辑代数的基本定律和恒等式
1. 基本公式
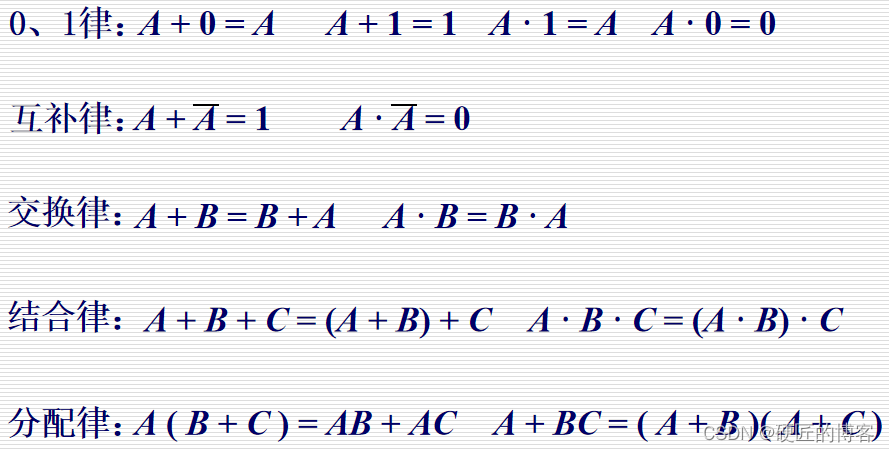

break the line,change the sign断掉线,改变符号
逻辑代数运算比较巧,公式把握不准最简行式,这也是逻辑代数方法的一个缺陷。化简取决于经验&运气
卡诺图才是章法,有道可循
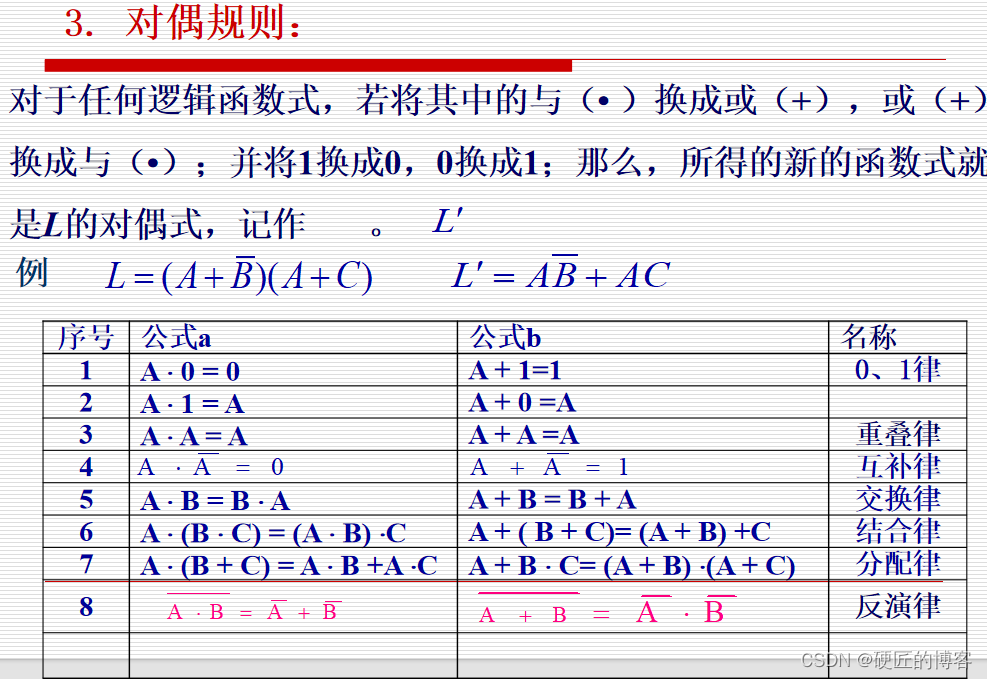
2.1.2 逻辑代数的基本规则


求反演表达式时,不能改变原始的运算优先级。(建议加上括号)
2.1.3 逻辑函数的变换及代数化简法
化简的意义:根据化简后的表达式构成的逻辑电路简单,可节省器 件,降低成本,提高工作的可靠性。
简化标准(最简的与-或表达式)
乘积项的个数最少(或门的个数少);
每个乘积项中包含的变量数最少(与门的输入端个数少)。
化简的主要方法:
1.公式法(代数法);
2.图解法(卡诺图法);

万能的与非门(或者其中的门),能够实现所有的门。从器件的简化程度,成本,可靠性(器件越少越可靠)上有提高
数理上的最简可能不是工程上的最简
数电中,每一级都会有相位差,应为每过一个门,都会有充电放电的过程,需要消耗能量,所以高速电路不允许太多的门串在一起,不然会引起相位变化严重
逻辑代数又称布尔代数。它是分析和设计现代数字逻辑电路不可缺少的数学工具。逻辑代数有一系列的定律、定理和规则,它用于对数学表达式进行处理,以完成对逻辑电路的化简、变换、分析和设计。
逻辑关系指的是事件产生的条件和结果之间的因果关系。在数字电路中往往是将事情的条件作为输入信号,而结果用输出信号表示。条件和结果的两种对立状态分别用逻辑“1” 和“0”表示。
卡诺图化简法:
2.2.1 最小项的定义及性质


PT项,与起来的就是PT项
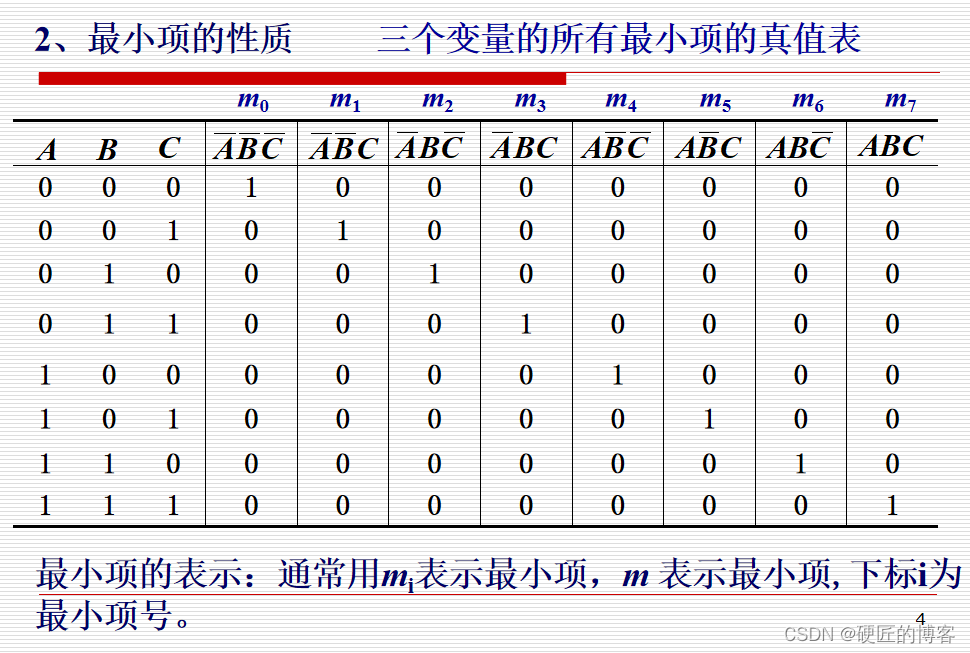
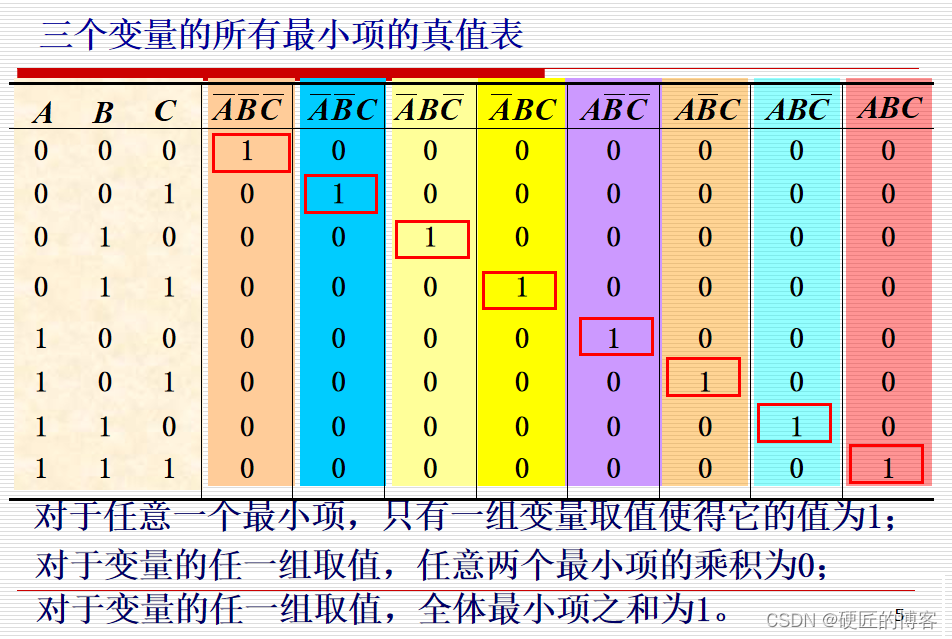
2.2.2 逻辑函数的最小项表达式

化成这种形式有利于计算机的处理
2.2.3 用卡诺图表示逻辑函数

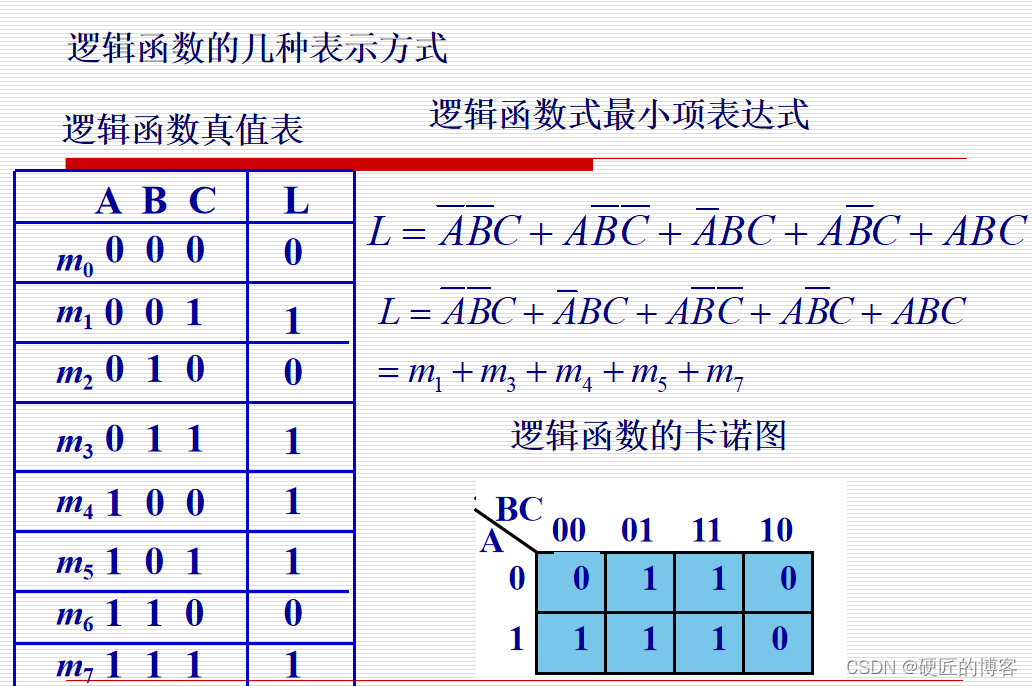
2.2.4 用卡诺图化简逻辑函数



卡诺图的图论基础
这一节课应该花2h认真地看一下,,同时用笔记进行标注才行,数电目前就此一节没做笔记