已知圆上两点P1,P2,坐标依次为
(
x
1
,
y
1
)
,
(
x
2
,
y
2
)
(x_1,y_1),(x_2,y_2)
(x1,y1),(x2,y2),圆的半径为
r
r
r,求圆心的坐标。
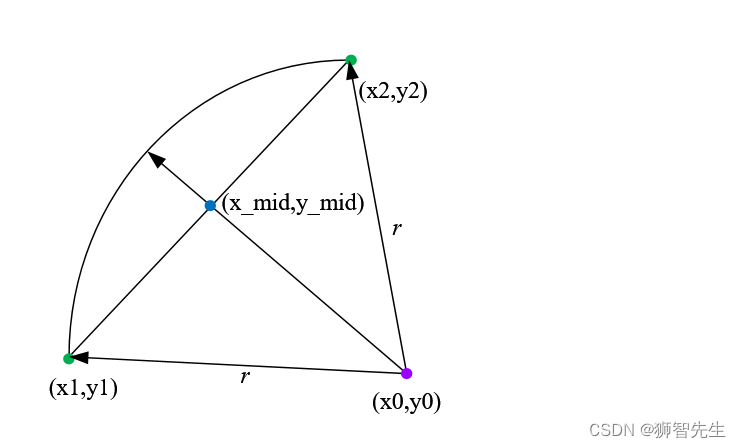
假定P1,P2为任意两点,则两点连成线段的中点坐标是
x
m
i
d
=
(
x
1
+
x
2
)
/
2
x_{mid} = (x_1+x_2)/2
xmid=(x1+x2)/2
y
m
i
d
=
(
y
1
+
y
2
)
/
2
y_{mid} = (y_1+y_2)/2
ymid=(y1+y2)/2
P1,P2连线的斜率是
k
=
(
y
1
−
y
2
)
/
(
x
1
−
x
2
)
k = (y_1-y_2)/(x_1-x_2)
k=(y1−y2)/(x1−x2)
P1,P2连线的垂线斜率为
m
=
−
1
/
k
m = -1/k
m=−1/k
则,圆心所在的直线方程是
y
−
y
m
i
d
=
m
∗
(
x
−
x
m
i
d
)
y-y_{mid} = m * (x - x_{mid})
y−ymid=m∗(x−xmid)
圆心
(
x
0
,
y
0
)
(x_0,y_0)
(x0,y0)同时满足
(
x
0
−
x
1
)
2
+
(
y
0
−
y
1
)
2
=
r
2
(x_0-x_1)^2+(y_0-y_1)^2=r^2
(x0−x1)2+(y0−y1)2=r2和
y
0
−
y
m
i
d
=
m
∗
(
x
0
−
x
m
i
d
)
y_0-y_{mid} = m * (x_0 - x_{mid})
y0−ymid=m∗(x0−xmid)
或
(
x
0
−
x
2
)
2
+
(
y
0
−
y
2
)
2
=
r
2
(x_0-x_2)^2+(y_0-y_2)^2=r^2
(x0−x2)2+(y0−y2)2=r2和
y
0
−
y
m
i
d
=
m
∗
(
x
0
−
x
m
i
d
)
y_0-y_{mid} = m * (x_0 - x_{mid})
y0−ymid=m∗(x0−xmid)
将直线方程
y
0
=
m
∗
(
x
0
−
x
m
i
d
)
−
y
m
i
d
y_0 = m*(x_0 -x_{mid})-y_{mid}
y0=m∗(x0−xmid)−ymid
代入圆的公式,
得到
(
x
0
−
x
1
)
2
+
[
m
∗
(
x
0
−
x
m
i
d
)
+
y
m
i
d
−
y
1
]
2
=
r
2
(x_0-x_1)^2+[m * (x_0-x_{mid})+y_{mid}-y_1]^2=r^2
(x0−x1)2+[m∗(x0−xmid)+ymid−y1]2=r2
展开,
x
0
2
−
2
x
0
x
1
+
x
2
2
+
m
2
x
0
2
+
2
m
x
0
∗
(
y
m
i
d
−
m
∗
x
m
i
d
−
y
1
)
+
(
y
m
i
d
−
m
∗
x
m
i
d
−
y
1
)
2
=
r
2
x_0^2-2x_0x_1+x_2^2+m^2x_0^2+2mx_0*(y_{mid}-m*x_{mid}-y_1)+(y_{mid}-m*x_{mid}-y_1)^2=r^2
x02−2x0x1+x22+m2x02+2mx0∗(ymid−m∗xmid−y1)+(ymid−m∗xmid−y1)2=r2
整理,
(
1
+
m
2
)
x
0
2
+
[
2
m
(
y
m
i
d
−
m
∗
x
m
i
d
−
y
1
)
−
2
x
1
]
∗
x
0
+
(
y
m
i
d
−
m
∗
x
m
i
d
−
y
1
)
2
+
x
1
2
−
r
2
=
0
(1+m^2)x_0^2+[2m(y_{mid}-m*x_{mid}-y_1)-2x_1]*x_0+(y_{mid}-m*x_{mid}-y_1)^2+x_1^2-r^2 = 0
(1+m2)x02+[2m(ymid−m∗xmid−y1)−2x1]∗x0+(ymid−m∗xmid−y1)2+x12−r2=0
令,
A
=
1
+
m
2
A= 1+m^2
A=1+m2
B
=
2
m
(
y
m
i
d
−
m
∗
x
m
i
d
−
y
1
)
−
2
x
1
B= 2m(y_{mid}-m*x_{mid}-y_1)-2x_1
B=2m(ymid−m∗xmid−y1)−2x1
C
=
(
y
m
i
d
−
m
∗
x
m
i
d
−
y
1
)
2
+
x
1
2
−
r
2
C= (y_{mid}-m*x_{mid}-y_1)^2+x_1^2-r^2
C=(ymid−m∗xmid−y1)2+x12−r2
则,
x
0
=
−
B
±
B
2
−
4
A
C
2
A
x_0=\frac{-B± \sqrt{B^2-4AC}}{2A}
x0=2A−B±B2−4AC
y
0
=
m
∗
(
x
0
−
x
m
i
d
)
+
y
m
i
d
y_0= m*(x_0-x_{mid})+y_{mid}
y0=m∗(x0−xmid)+ymid
x_1 = 2
y_1 = 4
x_2 = 4
y_2 = 2
r = 2
if (x_1 - x_2 == 0):
print('横坐标相同,求解可能出错')
exit()
else:
x_mid = (x_1 + x_2) / 2
y_mid = (y_1 + y_2) / 2
k = (y_1-y_2)/(x_1-x_2)
m = -1/k
A = 1 + m**2
B = 2 * m *(y_mid - m * x_mid - y_1)- 2 * x_1
C = (y_mid - m * x_mid - y_1)**2 + x_1**2 - r**2
print(A, B, C)
x_c1 = (-B + ((B**2-4*A*C)**0.5))/(2*A)
x_c2 = (-B - ((B**2-4*A*C)**0.5))/(2*A)
y_c1 = m * (x_c1 - x_mid) + y_mid
y_c2 = m * (x_c2 - x_mid) + y_mid
print('圆心坐标:',(x_c1,y_c1))
print('圆心坐标:',(x_c2,y_c2))
运行结果: