轨迹跟踪PID相关及前馈引入结果对比

news2024/11/17 16:04:53

1、前言：

        记录下给定一段轨迹如何实现跟踪控制，主要使用几个经典的方法进行对比。一些讨论的部分在代码中的注释部分。

        前馈控制可以在没有扰动和建模误差的理想条件下很好地跟踪期望输出，但在实际系统中，由于存在建模误差、外部扰动和初始条件误差，前馈控制无法完全消除系统误差。通常，前馈控制与反馈控制结合使用，通过反馈控制来补偿和校正误差，从而实现更精确和鲁棒的控制系统。

2、代码

% 参数设置
dt = 0.01;
T = 10;
time = 0:dt:T;

% 期望轨迹
x_d = cos(time); % x轨迹
y_d = sin(time); % y轨迹
z_d = 0.5 * time; % z轨迹

% 初始化位置
x_ff = zeros(size(time));
y_ff = zeros(size(time));
z_ff = zeros(size(time));

x_fb = zeros(size(time));
y_fb = zeros(size(time));
z_fb = zeros(size(time));

x_fffb = zeros(size(time));
y_fffb = zeros(size(time));
z_fffb = zeros(size(time));

x_pid = zeros(size(time));
y_pid = zeros(size(time));
z_pid = zeros(size(time));

x_apid = zeros(size(time));
y_apid = zeros(size(time));
z_apid = zeros(size(time));

x_apid_ff = zeros(size(time));
y_apid_ff = zeros(size(time));
z_apid_ff = zeros(size(time));
% x_apid_ff(1) = 1;

% PID参数
Kp = [20, 20, 20];
Ki = [0.1, 0.1, 0.1];
Kd = [0.01, 0.01, 0.01];

% 自适应PID参数
alpha = [20, 20, 20]; % 更新系数，控制参数的调整速度

% 初始点位置,说明初始误差的情况
x_ff(1)=.5;
x_fb(1) = .5;
x_fffb(1) = .5;
x_pid(1) = .5;
x_apid(1) = .5;
x_apid_ff(1)=.5;

% 初始化PID变量
integrated_error = [0, 0, 0];
previous_error = [0, 0, 0];


% 前馈控制
x_velocity_d = gradient(x_d, dt);%输出 FX 对应于 ∂F/∂x，即 x（水平）方向上的差分--近似导数--离散数据的梯度,way2---和diff(x_d) / dt同.但有较小误差
y_velocity_d = gradient(y_d, dt);
z_velocity_d = gradient(z_d, dt);
%{
% 数据： 说明gradient与diff使用之间的差别。diff由于是前向差分所以少一个数据。
x = 0:0.1:10;
y = sin(x);

% 使用 gradient 计算梯度
dydx_gradient = gradient(y, 0.1);

% 使用 diff 计算差分
dydx_diff = diff(y) / 0.1;
x_diff = x(1:end-1);

% 绘图
figure;
plot(x, y, 'r', 'LineWidth', 2); hold on;
plot(x, dydx_gradient, 'b--', 'LineWidth', 2);
plot(x_diff, dydx_diff, 'g-.', 'LineWidth', 2);
xlabel('X');
ylabel('Y and dY/dX');
legend('y = sin(x)', 'Gradient dy/dx', 'Diff dy/dx');
title('Comparison of Gradient and Diff');
grid on;

%}

for t = 1:length(time)-1
    % 前馈控制信号: 期望轨迹求导数way1；前馈输入为位置轨迹的差分或梯度
    % control_signal_x = -sin(time(t));
    % control_signal_y = cos(time(t));
    % control_signal_z = 0.5;
    % way2
% 获取期望速度（即前馈控制输入）way2
control_signal_x = x_velocity_d(t);
control_signal_y = y_velocity_d(t); 
control_signal_z =z_velocity_d(t);

    % 更新位置
    x_ff(t+1) = x_ff(t) + control_signal_x * dt;
    y_ff(t+1) = y_ff(t) + control_signal_y * dt;
    z_ff(t+1) = z_ff(t) + control_signal_z * dt;
end

% 反馈控制
for t = 1:length(time)-1
    % 当前误差
    error_x = x_d(t) - x_fb(t);
    error_y = y_d(t) - y_fb(t);
    error_z = z_d(t) - z_fb(t);

    % 反馈控制信号
    control_signal_x = Kp(1) * error_x;
    control_signal_y = Kp(2) * error_y;
    control_signal_z = Kp(3) * error_z;

    % 更新位置
    x_fb(t+1) = x_fb(t) + control_signal_x * dt;
    y_fb(t+1) = y_fb(t) + control_signal_y * dt;
    z_fb(t+1) = z_fb(t) + control_signal_z * dt;
end

% 前馈+反馈控制仅仅比例控制
for t = 1:length(time)-1
    % 当前误差
    error_x = x_d(t) - x_fffb(t);
    error_y = y_d(t) - y_fffb(t);
    error_z = z_d(t) - z_fffb(t);

    % 前馈控制信号：期望轨迹求导数way1的方式进行。
    feedforward_x = -sin(time(t));
    feedforward_y = cos(time(t));
    feedforward_z = 0.5;

    % 反馈控制信号
    feedback_x = Kp(1) * error_x;
    feedback_y = Kp(2) * error_y;
    feedback_z = Kp(3) * error_z;

    % 综合控制信号
    control_signal_x = feedforward_x + feedback_x;
    control_signal_y = feedforward_y + feedback_y;
    control_signal_z = feedforward_z + feedback_z;

    % 更新位置
    x_fffb(t+1) = x_fffb(t) + control_signal_x * dt;
    y_fffb(t+1) = y_fffb(t) + control_signal_y * dt;
    z_fffb(t+1) = z_fffb(t) + control_signal_z * dt;
end

% PID控制
for t = 1:length(time)-1
    % 当前误差
    error_x = x_d(t) - x_pid(t);
    error_y = y_d(t) - y_pid(t);
    error_z = z_d(t) - z_pid(t);

    % 积分误差
    integrated_error(1) = integrated_error(1) + error_x * dt;
    integrated_error(2) = integrated_error(2) + error_y * dt;
    integrated_error(3) = integrated_error(3) + error_z * dt;

    % 导数误差
    derivative_error_x = (error_x - previous_error(1)) / dt;
    derivative_error_y = (error_y - previous_error(2)) / dt;
    derivative_error_z = (error_z - previous_error(3)) / dt;

    % PID控制信号
    control_signal_x = Kp(1) * error_x + Ki(1) * integrated_error(1) + Kd(1) * derivative_error_x;
    control_signal_y = Kp(2) * error_y + Ki(2) * integrated_error(2) + Kd(2) * derivative_error_y;
    control_signal_z = Kp(3) * error_z + Ki(3) * integrated_error(3) + Kd(3) * derivative_error_z;

    % 更新位置
    x_pid(t+1) = x_pid(t) + control_signal_x * dt;
    y_pid(t+1) = y_pid(t) + control_signal_y * dt;
    z_pid(t+1) = z_pid(t) + control_signal_z * dt;

    % 更新前一个误差
    previous_error = [error_x, error_y, error_z];
end

% 自适应PID控制
for t = 1:length(time)-1
    % 当前误差
    error_x = x_d(t) - x_apid(t);
    error_y = y_d(t) - y_apid(t);
    error_z = z_d(t) - z_apid(t);

    % 自适应PID参数
    adaptive_Kp = Kp + alpha .* abs([error_x, error_y, error_z]);

    % 积分误差
    integrated_error(1) = integrated_error(1) + error_x * dt;
    integrated_error(2) = integrated_error(2) + error_y * dt;
    integrated_error(3) = integrated_error(3) + error_z * dt;

    % 导数误差
    derivative_error_x = (error_x - previous_error(1)) / dt;
    derivative_error_y = (error_y - previous_error(2)) / dt;
    derivative_error_z = (error_z - previous_error(3)) / dt;

    % 自适应PID控制信号
    control_signal_x = adaptive_Kp(1) * error_x + Ki(1) * integrated_error(1) + Kd(1) * derivative_error_x;
    control_signal_y = adaptive_Kp(2) * error_y + Ki(2) * integrated_error(2) + Kd(2) * derivative_error_y;
    control_signal_z = adaptive_Kp(3) * error_z + Ki(3) * integrated_error(3) + Kd(3) * derivative_error_z;

    % 更新位置
    x_apid(t+1) = x_apid(t) + control_signal_x * dt;
    y_apid(t+1) = y_apid(t) + control_signal_y * dt;
    z_apid(t+1) = z_apid(t) + control_signal_z * dt;

    % 更新前一个误差
    previous_error = [error_x, error_y, error_z];
end

%通过前馈控制提供初始控制信号，减少误差的产生；通过反馈控制修正剩余误差
% 自适应PID+前馈控制

% Ki=diag(zeros(3))';Kd=zeros(1,3);
% %此部分注释掉之后，只剩自适应P控制+前馈，效果要好于自适应PID+前馈和固定P反馈控制+前馈控制
%这是因为由于前馈控制的引入已经将误差引入到较小情况，而较小的误差时，ID控制反而会对误差处理有较大影响
% 应在不同的使积分和微分部分在特定情况下起作用，比如误差较大或较小时分别调整不同的权重。
% 前馈控制提供了基于期望轨迹的初始控制信号，若前馈控制信号已经较好地接近实际需求，比例控制的适应性调整就足够了。
% 而PID控制中的积分和微分部分可能会对前馈信号进行不必要的修正，反而影响效果。
for t = 1:length(time)-1
    % 当前误差
    error_x = x_d(t) - x_apid_ff(t);
    error_y = y_d(t) - y_apid_ff(t);
    error_z = z_d(t) - z_apid_ff(t);

    % 自适应PID参数
    adaptive_Kp = Kp + alpha .* abs([error_x, error_y, error_z]);

    % 积分误差
    integrated_error(1) = integrated_error(1) + error_x * dt;
    integrated_error(2) = integrated_error(2) + error_y * dt;
    integrated_error(3) = integrated_error(3) + error_z * dt;

    % 导数误差
    derivative_error_x = (error_x - previous_error(1)) / dt;
    derivative_error_y = (error_y - previous_error(2)) / dt;
    derivative_error_z = (error_z - previous_error(3)) / dt;

    % 自适应PID控制信号
    control_signal_x = adaptive_Kp(1) * error_x + Ki(1) * integrated_error(1) + Kd(1) * derivative_error_x;
    control_signal_y = adaptive_Kp(2) * error_y + Ki(2) * integrated_error(2) + Kd(2) * derivative_error_y;
    control_signal_z = adaptive_Kp(3) * error_z + Ki(3) * integrated_error(3) + Kd(3) * derivative_error_z;

    % 前馈控制信号
    feedforward_x = -sin(time(t));
    feedforward_y = cos(time(t));
    feedforward_z = 0.5;

    % 综合控制信号
    control_signal_x = feedforward_x + control_signal_x;
    control_signal_y = feedforward_y + control_signal_y;
    control_signal_z = feedforward_z + control_signal_z;

    % 更新位置
    x_apid_ff(t+1) = x_apid_ff(t) + control_signal_x * dt;
    y_apid_ff(t+1) = y_apid_ff(t) + control_signal_y * dt;
    z_apid_ff(t+1) = z_apid_ff(t) + control_signal_z * dt;

    % 更新前一个误差
    previous_error = [error_x, error_y, error_z];
end

% 自适应PID+前馈控制---上一部分的修改，用于根据误差动态调整对微分和积分控制，稍微比前面的自适应PID好，效果是误差在前馈+反馈P控制附近震荡
% previous_error = [0; 0; 0];
% integrated_error = [0; 0; 0];
% 
% for t = 1:length(time)-1
%     % 当前误差
%     error_x = x_d(t) - x_apid_ff(t);
%     error_y = y_d(t) - y_apid_ff(t);
%     error_z = z_d(t) - z_apid_ff(t);
% 
%     % 自适应PID参数
%     adaptive_Kp = Kp + alpha .* abs([error_x, error_y, error_z]);
% 
%     % 积分误差，条件限制积分项。使积分和微分部分在特定情况下起作用，比如误差较大或较小时分别调整不同的权重。
%     if abs(error_x) < 0.1
%         integrated_error(1) = integrated_error(1) + error_x * dt;
%     end
%     if abs(error_y) < 0.1
%         integrated_error(2) = integrated_error(2) + error_y * dt;
%     end
%     if abs(error_z) < 0.1
%         integrated_error(3) = integrated_error(3) + error_z * dt;
%     end
% 
%     % 导数误差，使用平滑处理
%     derivative_error_x = (error_x - previous_error(1)) / dt;
%     derivative_error_y = (error_y - previous_error(2)) / dt;
%     derivative_error_z = (error_z - previous_error(3)) / dt;
%     derivative_error_x = lowpass(derivative_error_x, 0.1, 1/dt); % 低通滤波
%     derivative_error_y = lowpass(derivative_error_y, 0.1, 1/dt);
%     derivative_error_z = lowpass(derivative_error_z, 0.1, 1/dt);
% 
%     % 自适应PID控制信号
%     control_signal_x = adaptive_Kp(1) * error_x + Ki(1) * integrated_error(1) + Kd(1) * derivative_error_x;
%     control_signal_y = adaptive_Kp(2) * error_y + Ki(2) * integrated_error(2) + Kd(2) * derivative_error_y;
%     control_signal_z = adaptive_Kp(3) * error_z + Ki(3) * integrated_error(3) + Kd(3) * derivative_error_z;
% 
%     % 前馈控制信号
%     feedforward_x = -sin(time(t));
%     feedforward_y = cos(time(t));
%     feedforward_z = 0.5;
% 
%     % 综合控制信号
%     control_signal_x = feedforward_x + control_signal_x;
%     control_signal_y = feedforward_y + control_signal_y;
%     control_signal_z = feedforward_z + control_signal_z;
% 
%     % 更新位置
%     x_apid_ff(t+1) = x_apid_ff(t) + control_signal_x * dt;
%     y_apid_ff(t+1) = y_apid_ff(t) + control_signal_y * dt;
%     z_apid_ff(t+1) = z_apid_ff(t) + control_signal_z * dt;
% 
%     % 更新前一个误差
%     previous_error = [error_x, error_y, error_z];
% end


% 绘制轨迹比较
figure;
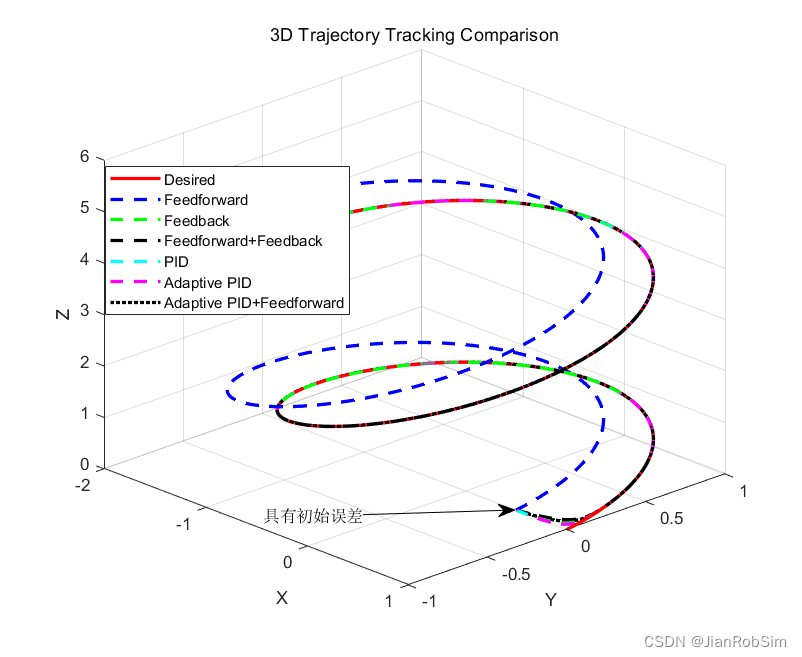
plot3(x_d, y_d, z_d, 'r', 'LineWidth', 2); hold on;
plot3(x_ff, y_ff, z_ff, 'b--', 'LineWidth', 2);
plot3(x_fb, y_fb, z_fb, 'g--', 'LineWidth', 2);
plot3(x_fffb, y_fffb, z_fffb, 'k--', 'LineWidth', 2);
plot3(x_pid, y_pid, z_pid, 'c--', 'LineWidth', 2);
plot3(x_apid, y_apid, z_apid, 'm--', 'LineWidth', 2);
plot3(x_apid_ff, y_apid_ff,z_apid_ff, 'k:', 'LineWidth', 2); % 自适应PID+前馈
xlabel('X');
ylabel('Y');
zlabel('Z');
legend('Desired', 'Feedforward', 'Feedback', 'Feedforward+Feedback', 'PID', 'Adaptive PID', 'Adaptive PID+Feedforward');
title('3D Trajectory Tracking Comparison');
grid on;

% 计算误差
error_ff = sqrt((x_d - x_ff).^2 + (y_d - y_ff).^2 + (z_d - z_ff).^2);
error_fb = sqrt((x_d - x_fb).^2 + (y_d - y_fb).^2 + (z_d - z_fb).^2);
error_fffb = sqrt((x_d - x_fffb).^2 + (y_d - y_fffb).^2 + (z_d - z_fffb).^2);
error_pid = sqrt((x_d - x_pid).^2 + (y_d - y_pid).^2 + (z_d - z_pid).^2);
error_apid = sqrt((x_d - x_apid).^2 + (y_d - y_apid).^2 + (z_d - z_apid).^2);
error_apid_ff = sqrt((x_d - x_apid_ff).^2 + (y_d - y_apid_ff).^2 + (z_d - z_apid_ff).^2);

% 绘制误差比较
figure;
plot(time, error_ff, 'b', 'LineWidth', 2); hold on;
plot(time, error_fb, 'g', 'LineWidth', 2);
plot(time, error_fffb, 'k', 'LineWidth', 2);
plot(time, error_pid, 'c', 'LineWidth', 2);
plot(time, error_apid, 'm', 'LineWidth', 2);
plot(time, error_apid_ff, 'k:', 'LineWidth', 2); % 自适应PID+前馈
xlabel('Time');
ylabel('Error');
legend('Feedforward', 'Feedback', 'Feedforward+Feedback', 'PID', 'Adaptive PID', 'Adaptive PID+Feedforward');
title('Error Comparison');
grid on;

3、结果【前馈的引入效果好很多】

4、其他参考学习链接
什么是前馈控制？_哔哩哔哩_bilibili

只用PID?加上前馈解决95%的问题！_哔哩哔哩_bilibili

PID控制器开发笔记之九：基于前馈补偿的PID控制器的实现_前馈补偿 c语言-CSDN博客

PID算法-从单级PID到单神经元自适应PID控制器 - 任囧 - 博客园 (cnblogs.com)

线性二次型调节器(LQR)原理详解-CSDN博客

前馈控制与MPC - Henry的博客 | Henry Blog (ldylab.cc)

本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如若转载，请注明出处：http://www.coloradmin.cn/o/1868007.html

如若内容造成侵权/违法违规/事实不符，请联系多彩编程网进行投诉反馈，一经查实，立即删除！

相关文章

解决微信小程序使用textarea输入框 type=“textarea“ 文本输入限制问题

解决微信小程序使用textarea输入框 type=“textarea“ 文本输入限制问题

出现的问题 type"textarea" 这个限制 微信小程序使用textarea , 输入字数大于140 时就输入不进去了 加入这个就解决了 maxlength"-1" <u-inputv-model"queryParams.orderIdTxt"border"true":focus"true":auto-height&q…
阅读更多...
学Prompt提示词，手撕大模型

学Prompt提示词，手撕大模型

最近&#xff0c;ChatGPT在网络上广受欢迎&#xff0c;以其独特的吸引力吸引了众多用户争相体验。 然而&#xff0c;各用户在使用后的感受和效果大不相同。有的用户欢欣鼓舞&#xff0c;将其视作珍宝&#xff0c;有的用户则感到平淡无奇&#xff0c;无甚趣味。有人将其作为生活…
阅读更多...
新能源汽车电机分类及工作原理

新能源汽车电机分类及工作原理

一、直流电机与交流电机 电机是一种将电能转换为机械能的设备&#xff0c;常见的有直流电机和交流电机两种类型。下面简要介绍它们的原理&#xff1a; 直流电机&#xff08;DC Motor&#xff09;: 原理: 直流电机的工作原理基于洛伦兹力定律&#xff0c;即电流通过导线时&…
阅读更多...
微信浏览器自动从http跳转到https的坑

微信浏览器自动从http跳转到https的坑

只要访问过同地址的https地址&#xff0c;就只能一直https了&#xff0c;无法再用https访问了&#xff0c;只能全站加上https才行。
阅读更多...
基于SOAR模型的面部情绪识别

基于SOAR模型的面部情绪识别

摘要 情绪表达在日常交流中起着特殊的作用&#xff0c;而检测情绪最重要的方法之一就是识别面部情绪状态。因此&#xff0c;自然人机交互的关键点是识别面部表情并根据感知到的情绪提供反馈。模型的实现涉及两个主要步骤。第一步是读取视频并将其转换为图像&#xff0c;然后对…
阅读更多...
Spring框架（一）

Spring框架（一）

1、服务端的三层开发 表现层、业务层&#xff08;spring就属于业务层&#xff09;、持久层 2、Spring是一个开放源代码的设计层面框架&#xff0c;它解决的是业务逻辑层和其他各层的松耦合问题&#xff0c;因此它将面向接口的编程思想贯穿整个系统应用 3、Spring的核心是控制…
阅读更多...
2024热门骨传导蓝牙耳机怎么选？超全的选购攻略附带好物推荐！

2024热门骨传导蓝牙耳机怎么选？超全的选购攻略附带好物推荐！

对于很多喜欢运动健身的小伙伴&#xff0c;在现在市面上这么多种类耳机的选择上&#xff0c;对于我来说的话还是很推荐大家去选择骨传导运动耳机的&#xff0c;相较于普通的入耳式蓝牙耳机&#xff0c;骨传导耳机是通过振动来传输声音的&#xff0c;而入耳式耳机则是通过空气传…
阅读更多...
计算机网络模型（OSI架构、TCP/IP架构）

计算机网络模型（OSI架构、TCP/IP架构）

OSI开放式系统互联 为什么会有通用的网络通信模型&#xff08;OSI、TCP/IP&#xff09;一、OSI&#xff08;1&#xff09;OSI 是什么&#xff08;2&#xff09;OSI 七层第七层、应用层第六层、表示层第五层、会话层第四层、传输层第三层、网络层第二层、数据链路层第一层、物理…
阅读更多...
【JD-GUI】MacOS 中使用Java反编译工具JD-GUI

【JD-GUI】MacOS 中使用Java反编译工具JD-GUI

希望文章能给到你启发和灵感&#xff5e; 如果觉得文章对你有帮助的话&#xff0c;点赞 关注 收藏 支持一下博主吧&#xff5e; 阅读指南 开篇说明概念理解一、基础环境说明1.1 硬件环境1.2 软件环境 二、下载与安装2.1 选择对应版本2.2 解压运行排除异常&#xff1a;2.3 关于…
阅读更多...
真实评测：可道云teamOS文件上传功能丝滑到爱不释手

真实评测：可道云teamOS文件上传功能丝滑到爱不释手

对于每日沉浸在图片与视频海洋中的媒体工作者而言&#xff0c;与海量的多媒体文件打交道几乎成了家常便饭。 文件的上传和存储&#xff0c;对他们而言&#xff0c;不仅仅是工作中的一个环节&#xff0c;更像是将一天的辛勤与付出妥善安置的仪式。无论是突发现场的精彩瞬间&am…
阅读更多...
每个 Node.js 开发人员都应该知道的13个库(下)

每个 Node.js 开发人员都应该知道的13个库(下)

7. Sequelize Mongoose是一个Node。基于js的MongoDB对象建模工具&#xff0c;通常被称为对象数据建模&#xff08;ODM&#xff09;库&#xff0c;它提供了诸如钩子、模型验证、连接和查询等功能。 Mongoose为应用程序数据提供了一个基于模式的解决方案&#xff0c;它在应用程…
阅读更多...
常微分方程算法之编程示例六-解一阶方程组（龙格-库塔法）

常微分方程算法之编程示例六-解一阶方程组（龙格-库塔法）

目录 一、研究问题 二、C++代码 三、计算结果 一、研究问题 本节我们采用龙格-库塔法（Runge-Kutta法）求解一阶方程组初值问题。 之前我们已经利用龙格-库塔法求解常微分方程问题，详见： 常微分方程算法之编程示例四（龙格-库塔法）-CSDN博客https://blog.csdn.net/L_pea…
阅读更多...
Windows11环境下安装Vmware Workstation 16的方法

Windows11环境下安装Vmware Workstation 16的方法

1、下载VMWare 从网盘下载 https://pan.baidu.com/share/init?surlUpcnqiRv6nUuzO0EOZ22zg 提取码&#xff1a;8888 2、安装VMware虚拟机 　　第1步&#xff1a;双击上面准备好的Vmware Workstation 16虚拟机软件安装包&#xff0c;即可看到如图所示的安装向导初始界面&#x…
阅读更多...
远程过程调用（RPC）

远程过程调用（RPC）

Hi~&#xff01;这里是奋斗的小羊&#xff0c;很荣幸您能阅读我的文章&#xff0c;诚请评论指点&#xff0c;欢迎欢迎 ~~ &#x1f4a5;&#x1f4a5;个人主页&#xff1a;奋斗的小羊 &#x1f4a5;&#x1f4a5;所属专栏&#xff1a;C语言 &#x1f680;本系列文章为个人学习…
阅读更多...
实际项目开发：Spring集成Redis，并实现短信登录功能

实际项目开发：Spring集成Redis，并实现短信登录功能

redis新手&#xff0c;学了几种基本数据类型&#xff0c;却不知道怎么使用&#xff1f; 总是一边学一边忘&#xff1f; 学会了Redis的大多数使用命令&#xff0c;却不知道如何在项目中使用&#xff1f; 本文将从实际出发&#xff0c;为大家解决这些问题。 我是蚊子码农&#xf…
阅读更多...
gin-vue -admin 初始化安装后 进入 后台首页报错

gin-vue -admin 初始化安装后 进入 后台首页报错

报错原因&#xff1a; 因为 我是使用的phpstudy 小皮的数据库 默认的是MySam 的引擎 mysql 引擎需要是 innoDB 解决办法 &#xff1a; 在linux 的环境下 配置一个数据库 &#xff0c; 我是用的是vmware 虚拟机
阅读更多...
【DC-DC升压电推剪方案】FP6277，FP6296电源升压芯片在电推剪中扮演着一个怎样的角色？带你深入了解电推剪的功能和应用及工作原理

【DC-DC升压电推剪方案】FP6277，FP6296电源升压芯片在电推剪中扮演着一个怎样的角色？带你深入了解电推剪的功能和应用及工作原理

随着人们对个人形象要求的不断提高&#xff0c;理发器作为一个必备的家居用品&#xff0c;也在不断进行技术升级。而其中的核心装备之一&#xff0c;电推剪理发器升压芯片FP6277、FP6296&#xff0c;正在引领着现代理发技术的突破。本文将给大家带来的是电推剪在传统意义上运用…
阅读更多...
V-Series Avalon-MM DMA Interface for PCIE IP核

V-Series Avalon-MM DMA Interface for PCIE IP核

目录 1. IP概述 2. Avalon-MM DMA Ports 3. 参数设置 3.1 系统设置 3.2 基址寄存器 (BAR) 设置 3.3 设备识别寄存器 3.4 PCI Express和PCI功能参数 3.4.1 Device Capabilities 3.4.2 Error Reporting 3.4.3 Link Capabilities 3.4.4 MSI and MSI-X Capabilities …
阅读更多...
开源 150 T 数据（2023年之前所有数据）

开源 150 T 数据（2023年之前所有数据）

开源 150 T 数据&#xff08;2023年之前所有数据&#xff09; 开源 150 T 数据生成大规模、高质量训练数据集 生成巨量数据 数据清洗和过滤 混合数据源 多级别训练和模型评估 探索新的训练策略多级别训练和模型评估探索新的训练策略 万卡 H100 集群训练 开源 150 T 数据 …
阅读更多...
B+树与索引解析

B+树与索引解析

文章目录 B树与索引简介几个关键点应用案例场景描述索引创建查询操作更新操作并发处理 Python代码示例 B树与索引简介 B树是一种在计算机科学中广泛使用的自平衡的树数据结构&#xff0c;它能保持数据排序&#xff0c;并且搜索、插入和删除操作的时间复杂度都是O(log n)。B树被…
阅读更多...
推荐文章
最新文章

Copyright @ 2022~2023