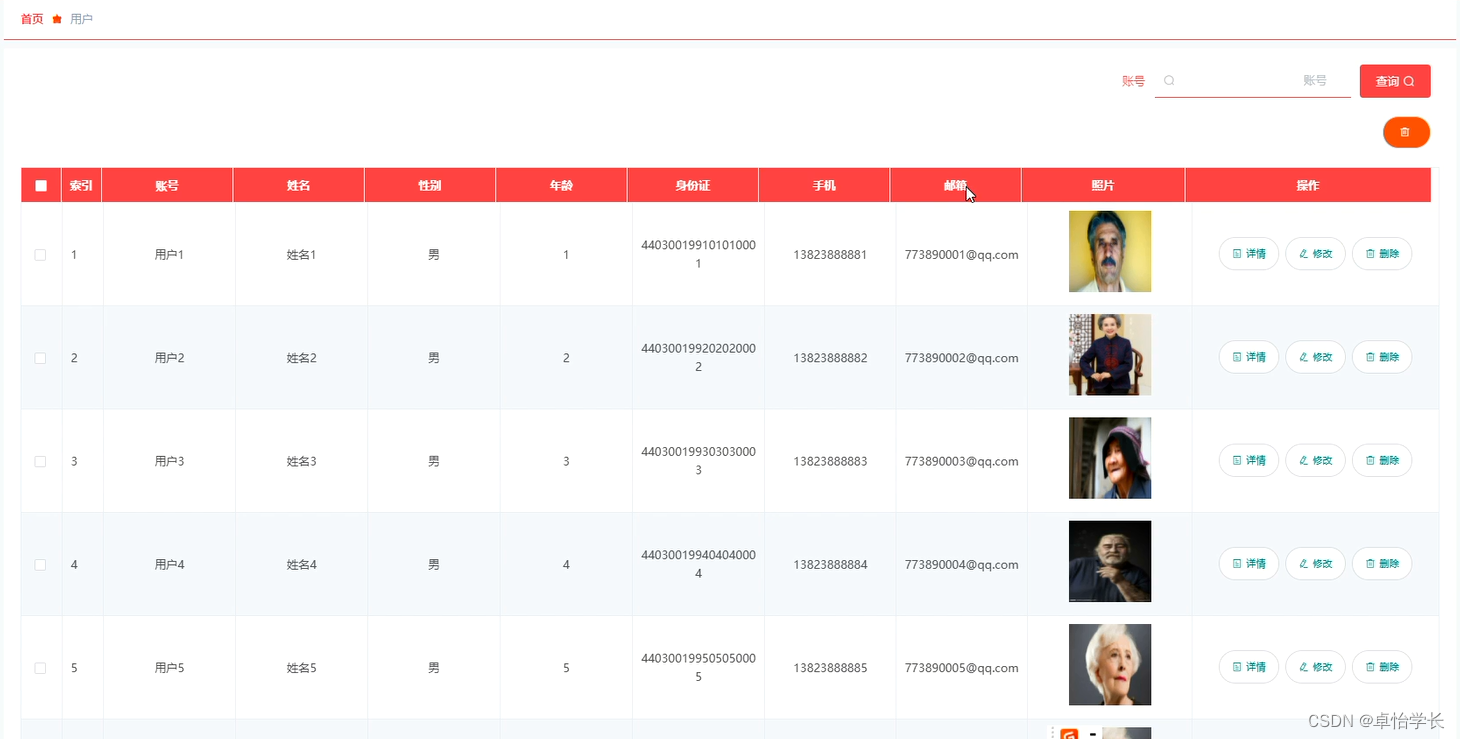
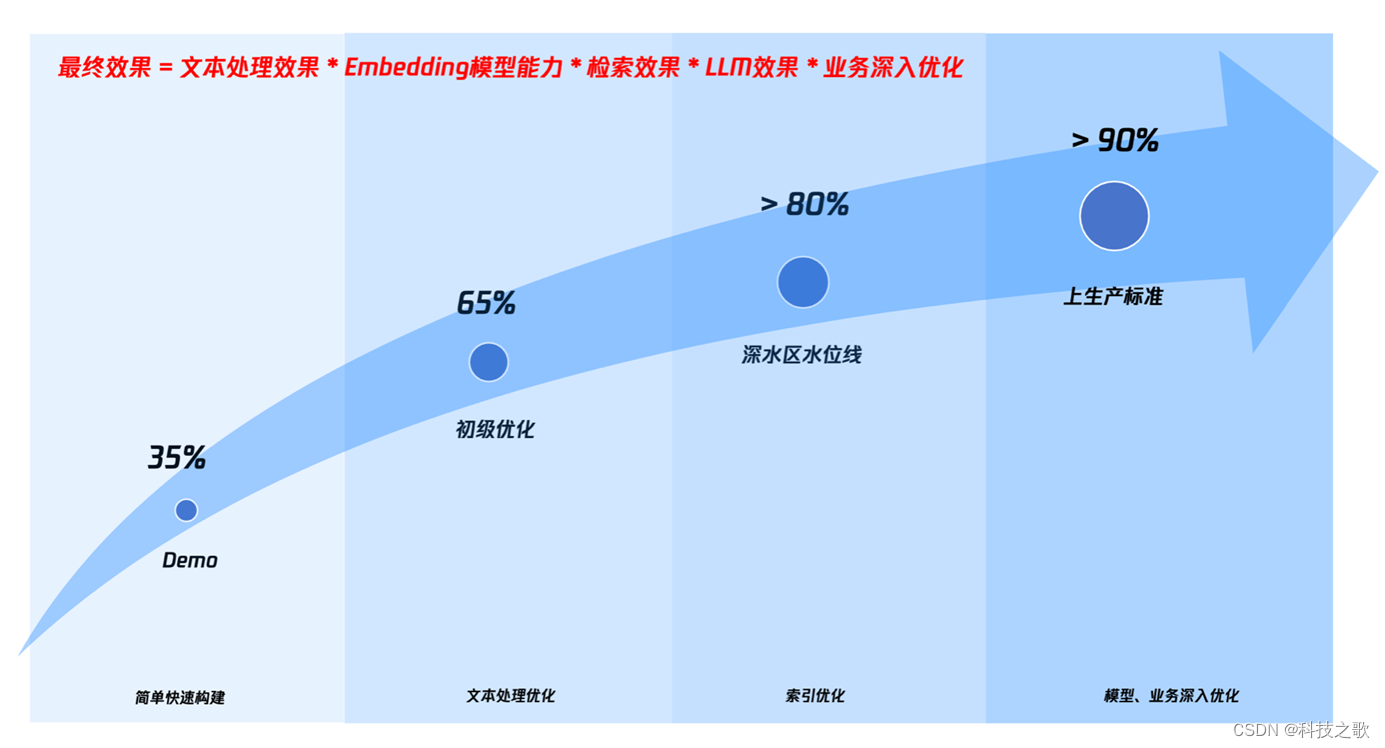
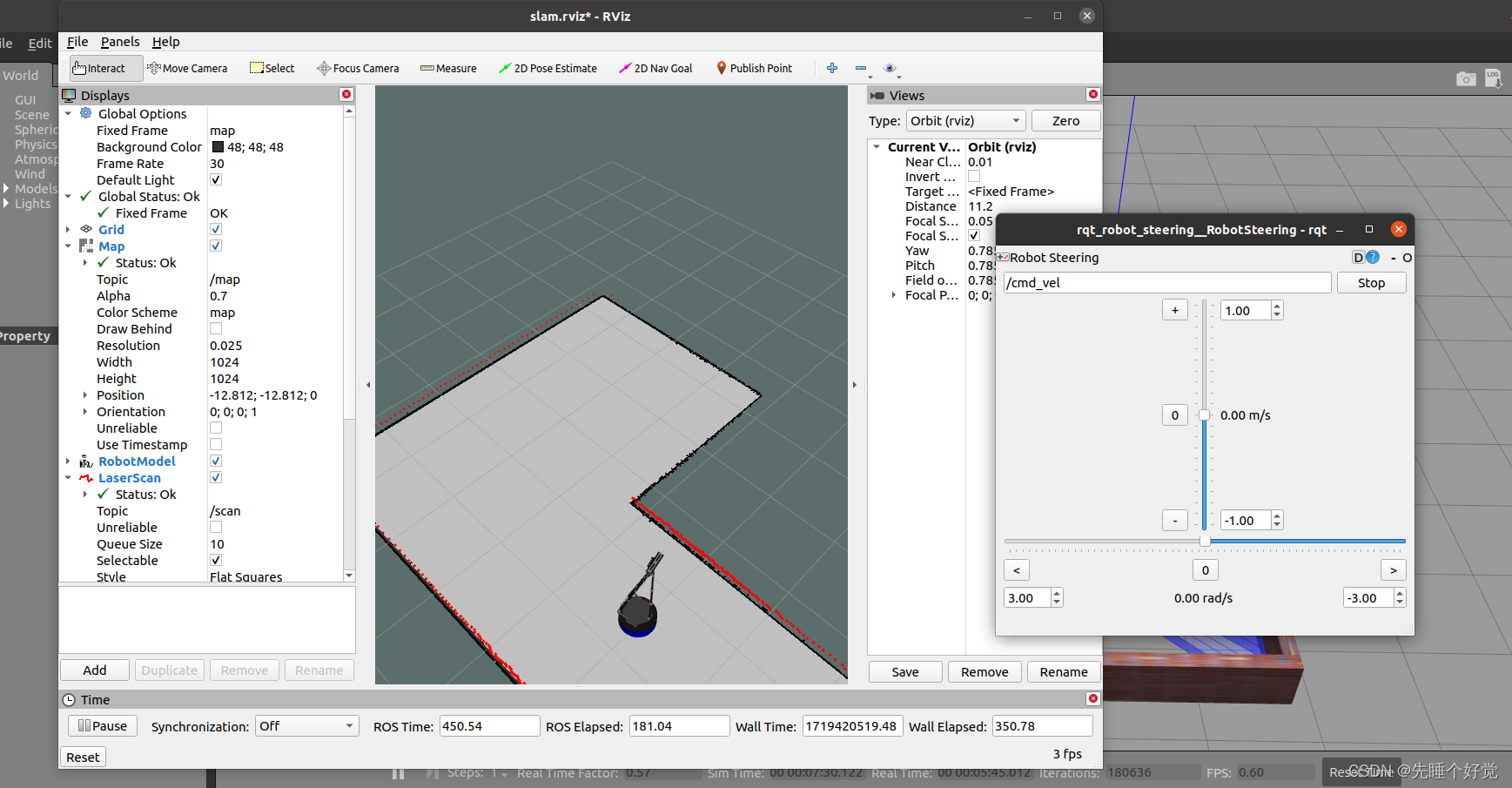
大家好,我是LvZi,今天带来
前缀和算法系列|概念讲解|应用场景|大量例题讲解
一.模版解析
1.一维前缀和
一维前缀和就是一个简单的dp问题
- 状态表示:
dp[i]:以i位置为结尾的所有元素的和 - 状态转移方程:
dp[i] = dp[i - 1] + arr[i]
链接:一维前缀和(模版题)
代码:
import java.util.Scanner;
// 注意类名必须为 Main, 不要有任何 package xxx 信息
public class Main {
public static void main(String[] args) {
Scanner in = new Scanner(System.in);
// 1.输入数据
int n = in.nextInt(), q = in.nextInt();
int[] arr = new int[n + 1];
for(int i = 1; i<= n; i++) arr[i] = in.nextInt();
// 2.使用dp表处理数据
long[] dp = new long[n + 1];
for(int i = 1; i<= n; i++) dp[i] = dp[i - 1] + arr[i];
// 3.打印数据
while(q > 0) {
int l = in.nextInt(), r = in.nextInt();
System.out.println(dp[r] - dp[l - 1]);
q--;
}
}
}
2.二维前缀和
同理,二位前缀和是一个简单的二维dp问题,难点在于dp表的状态转移方程和如何使用,需要进行推导

链接:二维前缀和
代码:
import java.util.Scanner;
// 注意类名必须为 Main, 不要有任何 package xxx 信息
public class Main {
public static void main(String[] args) {
Scanner in = new Scanner(System.in);
int n = in.nextInt(), m = in.nextInt(), q = in.nextInt();
int[][] arr = new int[n + 1][m + 1];
for(int i = 1; i <= n; i++){
for(int j = 1; j <= m; j++) {
arr[i][j] = in.nextInt();
}
}
// 预处理前缀和数组
long[][] dp = new long[n + 1][m + 1];
for(int i = 1; i <= n; i++){
for(int j = 1; j <= m; j++) {
dp[i][j] = dp[i - 1][j] + dp[i][j - 1] + arr[i][j] - dp[i - 1][j - 1];
}
}
// 使用前缀和数组
while(q > 0) {
int x1 = in.nextInt(), y1 = in.nextInt(), x2 = in.nextInt(), y2 = in.nextInt();
long ret = dp[x2][y2] - dp[x1 - 1][y2] - dp[x2][y1 - 1] + dp[x1 - 1][y1 - 1];
System.out.println(ret);
q--;
}
}
}
3.使用条件
前缀和算法是一种高效解决数组区间求和问题的技巧。它通过预处理数组,构建一个前缀和数组,使得任何区间的和可以在常数时间内计算出来。以下是一些你必须要掌握的核心概念和步骤:
核心概念
-
前缀和数组定义:
- 前缀和数组
prefix_sum是一个新数组,其中prefix_sum[i]表示原数组从第一个元素到第i个元素的和。 - 数学表示:
prefix_sum[i] = arr[0] + arr[1] + ... + arr[i-1]。
- 前缀和数组
-
构建前缀和数组:
- 前缀和数组的构建可以在
一次线性扫描中完成。 - 伪代码示例:
prefix_sum[0] = 0 for i in range(1, n+1): prefix_sum[i] = prefix_sum[i-1] + arr[i-1]
- 前缀和数组的构建可以在
-
区间和的计算:
- 一旦构建了前缀和数组,任何区间
[i, j]的和可以通过以下公式计算:sum[i:j] = prefix_sum[j+1] - prefix_sum[i]
- 这个计算过程是常数时间的
O(1)。这是前缀和算法快速的核心
- 一旦构建了前缀和数组,任何区间
必须掌握的步骤
-
理解并构建前缀和数组:
- 学会如何从原数组构建前缀和数组,包括处理边界情况(例如数组为空)。
-
使用前缀和数组进行区间求和:
- 熟练掌握如何通过前缀和数组高效计算任意区间的和。
-
优化特定问题:
- 掌握前缀和算法在解决特定问题时的应用,例如:
- 求数组中连续子数组的最大和。
- 求给定和的子数组(例如前缀和用于滑动窗口)。
- 掌握前缀和算法在解决特定问题时的应用,例如:
二.题目讲解
01.寻找数组的中间下标
链接:https://leetcode.cn/problems/find-pivot-index/description/
思路:
1.暴力解法
暴力解法很好想,就是每遍历到一个数,就去求他的rsum和lsum
public int pivotIndex(int[] nums) {
// 1.暴力解法
for(int i = 0; i < nums.length; i++) {
int lsum = 0, rsum = 0;
// 左边
for(int j = 0; j < i; j++) lsum += nums[j];
// 右边
for(int k = i+1; k < nums.length; k++) rsum += nums[k];
if(lsum == rsum) return i;
}
return -1;
}
2.前缀和算法
上述暴力解法最大的一个问题在于重复计算,
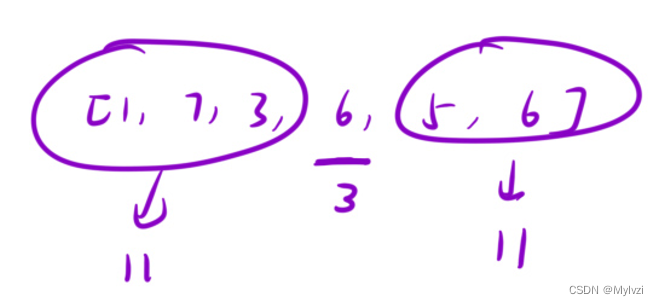
比如上图中,如果遍历到下标为3的数字6时,暴力解法需要先求lsum,即从下标为0的位置一直计算到6的前一个位置,但是实际上在求6的lsum时,下标0-1即(1,7)这两个数字的和在遍历到下标为2的数字3时已经求解过了,这里就发生了重复计算,
6的lsum可以直接使用(1,7)两个数字的和即3的lsum,再加上3本身就是6 的lsum
同理,6的rsum就是数字5的rsum再加上数字5本身
在这个过程中每遍历到一个数字就要保存前缀和和后缀和,可以通过创建出两个数组进行表示,设为f[]和g[]
这里面也有一个小的模版(思路+模版能强化我们的记忆):
- 状态表示 dp[i]表示什么意义
- 状态转移方程 dp[i]如何求解
f[i]表示 i 下标的数字的前缀和,f[i] = f[i - 1] + nums[i - 1]g[i]表示 i 下标的数字的后缀和,g[i] = g[i + 1] + nums[i + 1]
- 处理细节问题
如果是i == 0,f[0] = f[-1] + nums[-1],发生越界,实际上题目中已经告诉我们,下标为0的数字的前缀和为0,所以将f[0]设置为0,同理将g[n - 1]也设置为0
代码:
public int pivotIndex(int[] nums) {
// 1.设置两个数组
int n = nums.length;
int[] f = new int[n];
int[] g = new int[n];
// 2.细节问题
f[0] = 0; g[n - 1] = 0;
// 3.填数字
for(int i = 1; i < n; i++) f[i] = f[i - 1] + nums[i - 1];
for(int j = n - 2; j >= 0; j--) g[j] = g[j + 1] + nums[j + 1];
// 4.遍历数组
for(int i = 0; i < n; i++) {
if(f[i] == g[i]) return i;
}
return -1;
空间优化:本题比较简单,可以使用两个变量来维护左右和,代码如下
class Solution {
public int pivotIndex(int[] nums) {
int lsum = 0, rsum = 0;
for(int n : nums) rsum += n;
rsum -= nums[0];
if(rsum == lsum) return 0;
for(int i = 1; i < nums.length; i++) {
lsum += nums[i - 1];
rsum -= nums[i];
if(lsum == rsum) return i;
}
return -1;
}
}
02.除自身以外数组的乘积
本题和上题类似,暴力解法不做介绍,只介绍前缀和的思想
- 尽管这里面是乘积,不是和,但是思路一样,ans[i] 的结果就是i位置的左边所有数字的乘积 * 右边所有数字的乘积,也就是在遍历数组的过程中保存当前位置左边所有数字的乘积和右边所有数字的乘积
public int[] productExceptSelf(int[] nums) {
int n = nums.length;
int[] ans = new int[n];
int[] f = new int[n];
int[] g = new int[n];
// 处理细节问题
f[0] = 1;g[n - 1] = 1;
for(int i = 1; i < n; i++) {
f[i] = f[i - 1] * nums[i - 1];
}
for(int i = n - 2; i >= 0; i--) {
g[i] = g[i + 1] * nums[i + 1];
}
for(int i = 0; i< n; i++) {
ans[i] = f[i] * g[i];
}
return ans;
}
- 注意这里初始化dp表时应该初始化为1,初始化为0后续结果都是0
03.和为k的子数组
链接:https://leetcode.cn/problems/subarray-sum-equals-k/description/
思路:
1.暴力解法
暴力解法很容易想到,从下标为0的位置开始,一直加和到最后一个数字,统计在这个过程中出现的和为k的子数组的个数
public int subarraySum(int[] nums, int k) {
// 1.暴力解法
int cnt = 0;
for(int i = 0; i < nums.length; i++) {
int sum = 0;
for(int j = i; j < nums.length; j++) {
sum += nums[j];
if(sum == k) cnt++;
}
}
return cnt;
2.前缀和算法
同样的,本题中 也出现了重复计算的问题,我们的优化点就在这里,比如在遍历到下标为1的数字时,要从当前位置开始,一直加和到最后一个数字,但实际上这个区间内的和已经在遍历下标为0的数字时计算过了,能否一次遍历就得到结果呢
为了解决这个问题,我们可以创建出一个存储计算过程中结果的数组,每遍历到一个数字,就保存当前数字的和,那如何和本题 建立联系呢?下面的转化过程是重点
f[i]表示从0到i之间所有数字的和,假设存在两个下标 i 和 j(i < j) ,如果f[j] - f[i] = k,那么就证明nums数组中,i + 1到 j之间的所有数字和为k,由于f[i] = f[j] - k,此时就转换为统计从0开始一直到 i 位置和为f[j] - k的次数也就是每遍历到一个数字,就统计之间求和过程中出现过f[j] - k的次数(这样求更方便,转换思维)- 所以要绑定
和,出现次数之间的联系,使用哈希表建立 
Map<Integer,Integer> map = new HashMap<>();
map.put(0,1);// 处理整个数组的和为k的情况 此时就是寻找
int sum = 0, ret = 0;
for(int x : nums) {
sum += x;
ret += map.getOrDefault(sum - k, 0);
map.put(sum,map.getOrDefault(sum,0) + 1);
}
return ret;
}
04.和可被K整除的子数组个数
链接:和可被K整除的子数组个数
思路:
本题是蓝桥杯的一道原题,本题的难点在于同余定理,即两个数a , b,如果a mod k ==b mod k,那么(a - b) mod k== 0,在计算前缀和的过程中只需判断在这之前有没有相同的mod结果,如果有,则这两个区间的差值一定是可以被K整除的
对于i , j(i < j),如果f[j] mod k 的结果等于f[i] mod k的结果,则f[j] - f[i] mod k == 0,即[i + 1,j]的值可以被k整除

代码:
public int subarraysDivByK(int[] nums, int k) {
// 如果两个前缀和对于 mod k 的结果相同 则这两个前缀和的差值 mod k 一定 == 0
// 哈希表存放:前缀和 mod k的结果 以及结果出现的次数
// Map<Integer,Integer> map = new HashMap<>();
// map.put(0,1);// 初始化mod为0的情况出现的次数为1
int[] map = new int[k];
int sum = 0, cnt = 0;
map[0] = 1;
for(int x : nums) {
sum += x;
int mod = (sum % k + k) % k; // 处理负数取模的情况
cnt += map[mod];
map[mod]++;
// cnt += map.getOrDefault(mod,0);
// map.put(mod,map.getOrDefault(mod,0) + 1);
}
return cnt;
}
补充:对负数的理解

05.连续数组
链接:https://leetcode.cn/problems/contiguous-array/submissions/505261843/

代码:
public int findMaxLength(int[] nums) {
Map<Integer,Integer> map = new HashMap<>();// 映射关系为:sum 和 当前的下标
int n = nums.length;
map.put(0,-1);// 处理类似于[0,1]这样的情况
int sum = 0;
int len = 0;
for(int i = 0; i < n; i++) {
if(nums[i] == 0) sum -= 1;
else sum += 1;
if(map.containsKey(sum)) len = Math.max(len,i - map.get(sum));
else map.put(sum,i);
}
return len;
}
说明
- map.put(0,-1);// 处理类似于[0,1]这样的情况 ,当整个数组的和为0时,此时整个数组中所包含的0,1的数量相等,长度就是整个数组的长度,但是我们这里的核心是找之前是否有相同的值,对于这种情况,之前不存在=0的情况,是我们少考虑了边界情况,因为此时的下标已经走到了n - 1处,所以整个长度就是 此时的下标 - (-1)
- 如果两个位置的sum相同,只保留下标更小的那一个(这样才能保证长度是最长的),由于是从左往右遍历,所以遇到有相同的sum,当前下标的和就不保存
- 本题并不是预先就创建好dp数组,而是使用一个变量sum
动态维护前缀和,这也是此类问题常用的做法之一
06.矩阵区域和
链接:https://leetcode.cn/problems/matrix-block-sum/description/
本题是二维矩阵前缀和模版的一个应用,重点在于dp表的推导方式以及如何利用dp表
对于dp表来说,为了避免处理大量的边界问题,对dp表进行扩容
public int[][] matrixBlockSum(int[][] mat, int k) {
int n = mat.length;
int m = mat[0].length;
int[][] answer = new int[n][m];
int[][] dp = new int[n + 1][m + 1];
// 处理前缀和矩阵
for(int i = 1; i <= n; i++) {
for(int j = 1; j <= m; j++) {
dp[i][j] = dp[i - 1][j] + dp[i][j - 1] - dp[i - 1][j - 1] + mat[i - 1][j - 1];
}
}
// 处理返回值answer数组
for(int i = 0; i < n; i++) {
for(int j = 0; j < m; j++) {
int x1 = Math.max(i - k,0) + 1, y1 = Math.max(j - k,0) + 1;
int x2 = Math.min(i + k,n - 1) + 1, y2 = Math.min(j + k,m - 1) + 1;
answer[i][j] = dp[x2][y2] - dp[x1 - 1][y2] - dp[x2][y1 - 1] + dp[x1 - 1][y1 - 1];
}
}
return answer;
}
07.和为奇数的子数组数目
链接:https://leetcode.cn/problems/number-of-sub-arrays-with-odd-sum/
分析
最开始的想法就是暴力解法,但是时间复杂度为O(N^2),时间复杂度过高,且无法通过案例.由于是求区间和的问题,想办法使用前缀和,本题主要用到一个数学性质,且看下图分析

- 题目求的是
和为奇数的子数组的数目,我们只要保证f[j]和f[i]的奇偶性不同,就能保证[i+1,j]这个区间内部的和为奇数 f[j]为偶数:只要f[i]为奇数就行,统计j位置之前奇数和的数目即可f[j]为奇数:只要f[i]为偶数就行,统计j位置之前偶数和的数目即可
代码:
class Solution {
int MOD = (int)(1e9 + 7);
public int numOfSubarrays(int[] arr) {
int sum = 0, odd_cnt = 0, even_cnt = 1, ret = 0;
for(int x : arr) {
sum += x;
if(sum % 2 == 0) {// 偶数
ret += odd_cnt;// 统计j位置之前奇数的数目
++even_cnt;
}else {
ret += even_cnt;// 统计j位置之前偶数的数目
++odd_cnt;
}
ret %= MOD;
}
return ret % MOD;
}
}
8.连续的子数组和
链接:https://leetcode.cn/problems/continuous-subarray-sum/
分析
- 其实一眼看去和上面的
和可被k整除子数组和相似,使用同余定理,判断是否存在两个modK结果相同的和即可 - 注意本题有
区间长度的限制,所以需要使用哈希表建立mod的结果和下标之间的映射关系
代码:
class Solution {
public boolean checkSubarraySum(int[] nums, int k) {
int n = nums.length, sum = 0;
Map<Integer, Integer> hash = new HashMap<>();// 建立mod 与 下标之间的映射关系
hash.put(0, -1);// 处理数组和%k==0的情况
for(int i = 0; i < n; i++) {
sum += nums[i];
int mod = sum % k;
if(hash.containsKey(mod)) {
int j = hash.get(mod);
if(i - j >= 2)
return true;
}else
hash.put(mod,i);
}
return false;
}
}
细节
- hash.put(0, -1);整个数组和%k==0,往前找可能根本找不到0的情况,此时区间长度就是整个数组的长度,
(n - 1) - (-1) == n,走到最后下标是n-1,只有减去-1才是正确答案 - 当具有两个相同mod值时,保留i最小的那个
09.最大好子数组和
链接:最大好子数组和
分析
- 分析题目:要求的是满足
好子数组条件的子数组的最大和,暴力解法很容易想到,时间复杂度为O(N^2) - 分析暴力解法时间复杂度过高的原因,在求和的时候进行了大量的重复运算,既然是求区间和,就可以使用
前缀和的思想优化为线性时间
思路:
- 遍历整个数组,每遍历到一个数字就判断是否有满足条件的数
|nums[i] - nums[j]| == k(使用哈希表存储nums[i]和i),如果存在,则计算这两个元素之间的区间和; - 计算元素区间和的快速方法就是使用
前缀和数组,则两个下标(i, j)的区间和能快速求出,注意i为0的情况,此时就是从0到j的区间和 - 当有重复出现的key值时,应该如何保留?–
贪心算法 - 题目求解的
"最大区间和"ret的计算公式是dp[j] - dp[i](j > i),当dp[i]尽可能小的时候 ret才会尽可能大 所以要保留前缀和较小的那个key的下标
代码:
class Solution {
public long maximumSubarraySum(int[] nums, int k) {
int n = nums.length;
long ret = Long.MIN_VALUE;
long[] dp = new long[n + 1];
for(int i = 1; i <= n; i++) dp[i] = dp[i - 1] + nums[i - 1];
Map<Integer, Integer> hash = new HashMap<>();// 建立nums[i]和i之间的映射关系
for(int i = 0; i < n; i++) {
int n1 = nums[i] + k, n2 = nums[i] - k;
// 判断是否存在"符合题目条件"的元素,如果存在,则计算这两个元素之间的区间和
if(hash.containsKey(n1)) ret = Math.max(ret, dp[i + 1] - dp[hash.get(n1)]);
if(hash.containsKey(n2)) ret = Math.max(ret, dp[i + 1] - dp[hash.get(n2)]);
// 贪心算法 当有重复出现的key值时,应该如何保留?
// 题目求解的"最大区间和" ret的计算公式是dp[j] - dp[i](j > i)
// 当dp[i]尽可能小的时候 ret才会尽可能大 所以要保留前缀和较小的那个key的下标
if(hash.containsKey(nums[i])) {// 之前已经存在 判断是否需要更新下标 贪心算法
int curIndex = i, preIndex = hash.get(nums[i]);
int index = dp[curIndex] < dp[preIndex] ? curIndex : preIndex;// 保留小的
hash.put(nums[i], index);
}else {// 不存在直接建立映射关系即可
hash.put(nums[i], i);
}
}
return ret == Long.MIN_VALUE ? 0 : ret;
}
}
10.表现良好的时间段
链接:表现良好的时间段
分析
- 找
劳累时间>非劳累时间的最长子数组 - 本题不能使用滑动窗口算法,因为
数组+所求不具有单调性 - 大于8小时的时间我们当做1,小于或等于8小时的工作时间当做-1,使用前缀和的思想求解
- 转化为
区间和大于0的最长子数组,注意本题是最长,之前做过一道题目是区间和大于target的最短子数组(滑动窗口解决), - 遍历整个数组,假设遍历到j位置,前缀和为
f[j],要想存在下标i使得区间[i+1,j]的和大于0,则要存在比f[j]小的区间和f[i]

代码:
class Solution {
public int longestWPI(int[] hours) {
// 学会转化的思路
// 想到使用1和-1来代替工作时间是否大于8小时
// 接下来的如何寻找答案没想到
int n = hours.length, sum = 0, ret = 0;
Map<Integer, Integer> hash = new HashMap<>();
for(int i = 0; i < n; i++) {
sum += hours[i] > 8 ? 1 : -1;
if(sum > 0) ret = Math.max(ret, i + 1);
else {// <0
if(hash.containsKey(sum - 1)) {
ret = Math.max(ret, i - hash.get(sum - 1));
}
}
if(!hash.containsKey(sum)) hash.put(sum, i);// 保留下标较小的那个
}
return ret;
}
}
相似题目
链接:字母与数字
代码:
class Solution {
public String[] findLongestSubarray(String[] arr) {
// 相同的话就是判断是否具有相同的sum
// 如果有就更新区间下标
int n = arr.length, sum = 0, start = 0, end = 0;
Map<Integer, Integer> hash = new HashMap<>();
hash.put(0, -1);
for(int i = 0; i < n; i++) {
sum += arr[i].charAt(0) >= 'A' ? 1 : -1;// 字母加1 数字减一
if(hash.containsKey(sum)) {
if(i - hash.get(sum) > end - start + 1) {// end - start + 1才是真正的区间长度
start = hash.get(sum) + 1;
end = i;
}
}else {
hash.put(sum, i);
}
}
if(start == 0 && end == 0) return new String[]{};
return Arrays.copyOfRange(arr, start, end + 1);
}
}
11.异或前缀和
链接:https://leetcode.cn/problems/xor-queries-of-a-subarray/description/
分析
- 分析题目,返回的结果是
[l,r]区间所有元素的异或结果 - 最简单的做法就是从
l-r暴力异或每一个数字,时间复杂度为O(N) - 分析发现暴力做法的冗余的地方和求任意区间的和相同,故本题也可以使用前缀和数组
- 使用前缀和数组dp,
dp[i]表示[0,i]区间内部所有元素的异或结果 - 如何使用前缀和数组呢?也是根据
^(异或)的性质,a^a = 0

代码:
class Solution {
public int[] xorQueries(int[] arr, int[][] queries) {
int m = queries.length, n = arr.length;
int[] ret = new int[m], dp = new int[n + 1];
for(int i = 1; i <= n; i++)
dp[i] = dp[i - 1] ^ arr[i - 1];// 存储异或结果
// O(N + M)
for(int i = 0; i < m; i++) {
int start = queries[i][0], end = queries[i][1];
ret[i] = dp[end + 1] ^ dp[start];// 注意arr的下标和dp的下标存在加1的关系
}
return ret;
}
}
12.构建回文串检测(较难)
链接:https://leetcode.cn/problems/can-make-palindrome-from-substring/description/
分析
- 对于每次询问,必须在
至多改变k个字母的前提下,使得子串成为回文子串
1.关于修改回文子串的一个规律
- 如果子串内部的每个字符出现的次数都是偶数,天然就是回文子串,不需要进行任何操作
- 如果子串内部有一个字符出现的次数为奇数(假设为a),那么可以将a当做中心,此子字符串仍然是回文子串,同样不需要进行任何操作
- 如果子串内部有两个字符出现的次数为奇数(假设为a,b),需要
一次操作(将b替换成a)才能使子串为回文子串 - 如果子串内部有三个字符出现的次数为奇数(假设为a,b,c),需要
一次操作(将c替换成b,这样b,c出现的次数都是偶数)才能是子串为回文子串 - 如果子串内部有四个字符出现的次数为奇数(假设为a,b,c,d),需要
两次操作(将c替换成b,将d替换为a,此时a,b,c,d出现的次数都为偶数)才能是子串为回文子串
结论:
如果一个字符串内部出现次数为奇数的字符的个数为m,那么至多需要
m/2次操作就能使该字符串转换为回文串

2.使用前缀和数组统计每个子串内部各个字符出现的次数
- 知道上述规律,关键在于如何快速得到子串内部各个字符出现的次数?最简单的想法就是暴力解法,遍历每一个字符和其出现的次数,最后在统计出现次数为奇数的字符个数
- 此外还可以使用
前缀和数组统计,具体来说使用一个dp表 dp[i][c]:表示[0,i]区间内部,字符c出现的次数

代码:
class Solution {
public List<Boolean> canMakePaliQueries(String s, int[][] queries) {
// 1.构建前缀和数组
int n = s.length();
int[][] dp = new int[n + 1][26];
for(int i = 1; i <= n; i++) {
for(int j = 0; j < 26; j++)
dp[i][j] = dp[i - 1][j];
dp[i][s.charAt(i - 1) - 'a']++;
}
// 2.根据查询返回结果
List<Boolean> ret = new ArrayList<>();
for(int[] query : queries) {
int l = query[0], r = query[1], k = query[2];
int oddCnt = 0;
for(int j = 0; j < 26; j++)
if((dp[r + 1][j] - dp[l][j]) % 2 != 0)
oddCnt++;
ret.add(oddCnt / 2 <= k);
}
return ret;
}
}
优化一
- 我们只关注每个字符出现次数的奇偶性,并不关注具体出现了多少次
- 使用0表示出现偶数次 1表示出现奇数次
代码:
class Solution {
public List<Boolean> canMakePaliQueries(String s, int[][] queries) {
// 优化1:我们只关注每个字符出现次数的奇偶性,并不关注具体出现了多少次
// 使用0表示出现偶数次 1表示出现奇数次
int n = s.length();
int[][] dp = new int[n + 1][26];
for(int i = 1; i <= n; i++) {
dp[i] = dp[i - 1].clone();
dp[i][s.charAt(i - 1) - 'a']++;
dp[i][s.charAt(i - 1) - 'a'] %= 2;
}
// 2.根据查询返回结果
List<Boolean> ret = new ArrayList<>();
for(int[] query : queries) {
int l = query[0], r = query[1], k = query[2];
int oddCnt = 0;
for(int j = 0; j < 26; j++)
oddCnt += (dp[r + 1][j] == dp[l][j] ? 0 : 1);// 奇偶性不同 相减一定为奇数 表示该字符出现的次数为奇数
ret.add(oddCnt / 2 <= k);
}
return ret;
}
}
优化2
-
考虑到只有
0,1两个数字,在判断字符出现次数是否为奇数时,我们通过判断l,r的奇偶性是否相同来抉择 -
如果奇偶性相同,则字符出现次数为偶数,此时要么全是1,要么全是0,此时异或的结果一定为0
-
如果奇偶性不同,则字符出现次数为奇数,此时一个是1,一个是0,此时异或的结果一定为1
-
可以使用异或运算代替奇偶性的判断
-
同时在dp表进行初始化时也可以进行
异或运算的优化,此时遍历到字符s[i],该位置字符出现的次数应该+1 -
如果上一层出现的次数为0,本层应该变为1(偶数变奇数),使用
0^1同样可以完成此操作 -
同理,如果上次层出现的次数为1,本层应该为2(奇数变偶数),使用
1^1 = 0同样可以完成此操作
代码:
class Solution {
public List<Boolean> canMakePaliQueries(String s, int[][] queries) {
// 优化2:使用异或的性质(无进位加法)
int n = s.length();
int[][] dp = new int[n + 1][26];
for(int i = 1; i <= n; i++) {
dp[i] = dp[i - 1].clone();
dp[i][s.charAt(i - 1) - 'a'] ^= 1;
}
// 2.根据查询返回结果
List<Boolean> ret = new ArrayList<>();
for(int[] query : queries) {
int l = query[0], r = query[1], k = query[2];
int oddCnt = 0;
for(int j = 0; j < 26; j++)
oddCnt += dp[r + 1][j] ^ dp[l][j];
ret.add(oddCnt / 2 <= k);
}
return ret;
}
}
优化3
- 考虑到大小为26的数组只存储
0,1,可以将其压缩到一个数中,也就是经典的二进制压缩 - 对于一个整数来说,大小为4个字节,即
32个比特位,每一个比特位要么是0,要么是1,所以考虑将0,1存储到数字中 - 具体来说,使用最低位标识字符a出现次数的奇偶性,如果是0表示出现次数为偶数次,如果是1,表示出现次数为奇数次;同理,使用第二位表示字符b出现次数的奇偶性…以此类推
- 当前字符是
s[i],上一次出现的次数为0,那么本层出现的次数应该为1,如何通过异或实现呢?只需要让上一个层的数字异或1 << (s[i] - 'a')即可,这一位就从0-1;如果上一层是1,本层就变为0(还是^的运算性质) - 那么如何统计
[l, r]区间内部各个字符出现的次数呢?注意,异或运算是并行运算的,每一位都在进行异或运算,用dp[r + 1] ^ dp[l],得到结果中1的个数就是此区间内部字符出现次数为奇数的个数(只有1和0异或的结果才是1,此时表示奇偶性不同)
代码:
class Solution {
public List<Boolean> canMakePaliQueries(String s, int[][] queries) {
int n = s.length();
int[] dp = new int[n + 1];
for (int i = 0; i < n; i++) {
int bit = 1 << (s.charAt(i) - 'a');
dp[i + 1] = dp[i] ^ bit; // 该比特对应字母的奇偶性:奇数变偶数,偶数变奇数
}
List<Boolean> ret = new ArrayList<>();
for (int[] q : queries) {
int left = q[0], right = q[1], k = q[2];
int m = Integer.bitCount(dp[right + 1] ^ dp[left]);
ret.add(m / 2 <= k);
}
return ret;
}
}
总结
- 前缀和算法快的原因在于
在常数时间内求出任意区间的和,常规求取区间和的做法是依次遍历 - 前缀和算法根据形式可分为
一维和二维,本质上都是动态规划问题 - 构建dp表简单,难点在于如何使用创建的前/后缀和数组
- 优化:可以使用变量替代数组,进行空间优化
- 不仅仅是数学意义上的
前缀和,还可以用于统计字符出现的次数,用于快速查找之前遍历过程中的某一个量,经常用于解决类似于最长xxxx区间问题 - 除了预先准备好前缀和数组,还经常使用的做法是使用一个变量sum来动态的维护前缀和








![[JS]DOM事件](https://img-blog.csdnimg.cn/img_convert/d084a85e43239bdd0538ffca877dff82.png)