LeetCode 算法：验证二叉搜索树 c++

news2024/11/18 7:29:35

原题链接🔗：验证二叉搜索树
难度：中等⭐️⭐️

题目

给你一个二叉树的根节点 root ，判断其是否是一个有效的二叉搜索树。

有效二叉搜索树定义如下：

节点的左子树只包含小于当前节点的数。
节点的右子树只包含大于当前节点的数。
所有左子树和右子树自身必须也是二叉搜索树。

示例 1：

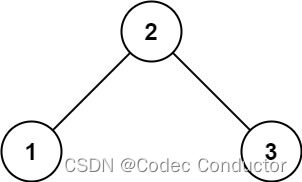
输入：root = [2,1,3] 输出：true

示例 2：

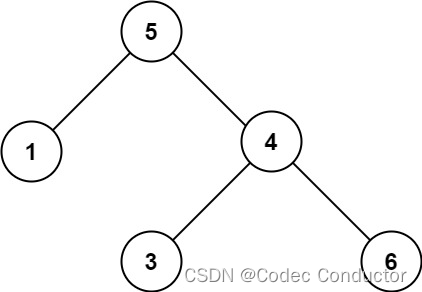
输入：root = [5,1,4,null,null,3,6] 输出：false
解释：根节点的值是 5 ，但是右子节点的值是 4 。

提示：

树中节点数目范围在[1, 10⁴] 内
-2³¹ <= Node.val <= 2³¹ - 1

题解

解题思路:

验证一棵二叉树是否为二叉搜索树（BST）是算法面试中常见的问题。二叉搜索树具有以下性质：

若任意节点的左子树不为空，则左子树上所有节点的值均小于它的节点值。
若任意节点的右子树不为空，则右子树上所有节点的值均大于它的节点值。
任意节点的左、右子树也可能有空二叉树，并且都同时为空。
左子树和右子树也分别为二叉搜索树。

以下是验证二叉搜索树的几种解题思路：

中序遍历
二叉搜索树的中序遍历结果应该是一个递增的序列。因此，可以通过中序遍历来验证二叉树是否为BST。

对二叉树进行中序遍历，将遍历结果存储在一个数组中。
检查数组中的元素是否是递增的。

这种方法的时间复杂度是O(n)，空间复杂度也是O(n)，因为需要存储所有的节点值。

递归检查
使用递归函数，同时检查当前节点的值是否在允许的范围内。

定义一个变量lower和upper来存储当前节点允许的最小值和最大值，初始时可以是负无穷和正无穷。
在递归函数中，首先检查当前节点的值是否在lower和upper之间。
然后递归地对左子树和右子树调用函数，同时更新lower和upper的值。

这种方法的时间复杂度是O(n)，因为它只需要遍历一次所有节点，空间复杂度是O(h)，其中h是树的高度，因为递归栈的深度。

迭代法
使用迭代法代替递归，可以避免递归带来的栈溢出问题，特别是对于非常深的树。

使用一个栈来存储节点，从根节点开始，按照二叉树的遍历顺序（例如先序、中序或后序）将节点压入栈中。
同时维护一个变量来记录前一个节点的值。
当迭代到下一个节点时，检查它是否符合BST的顺序性。

这种方法的时间复杂度同样是O(n)，空间复杂度也是O(n)，因为最坏情况下，栈可能需要存储所有的节点。

Morris遍历
Morris遍历是一种不需要额外空间的遍历方法，可以用于验证BST。

使用Morris遍历遍历二叉树，同时检查节点的值是否递增。
Morris遍历通过在树中添加临时指针来实现，不需要使用栈或数组。

这种方法的时间复杂度是O(n)，空间复杂度是O(1)，因为它不需要额外的存储空间。

每种方法都有其优缺点，你可以根据具体情况选择最合适的方法。例如，如果树非常深，递归可能会导致栈溢出，此时可以使用迭代法或Morris遍历。如果需要额外的空间不是问题，中序遍历是一个简单直观的方法。

递归法

复杂度：时间复杂度是O(n)，因为它只需要遍历一次所有节点，空间复杂度是O(h)，其中h是树的高度，因为递归栈的深度。
c++ demo：

#include <iostream>
#include <limits>

struct TreeNode {
    int val;
    TreeNode* left;
    TreeNode* right;
    TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
};

class Solution {
public:
    bool isValidBST(TreeNode* root) {
        return validate(root, std::numeric_limits<long>::min(), std::numeric_limits<long>::max());
    }

private:
    bool validate(TreeNode* node, long min, long max) {
        if (!node) return true; // 空节点是有效的

        // 检查当前节点的值是否在合适的范围内
        if (node->val <= min || node->val >= max) return false;

        // 递归地验证左子树和右子树
        // 左子树的所有值必须小于当前节点的值
        // 右子树的所有值必须大于当前节点的值
        return validate(node->left, min, node->val) &&
            validate(node->right, node->val, max);
    }
};

int main() {
    Solution solution;
    // 构建一个示例二叉搜索树
    TreeNode* root = new TreeNode(2);
    root->left = new TreeNode(1);
    root->right = new TreeNode(3);

    // 验证二叉搜索树
    bool result = solution.isValidBST(root);

    std::cout << (result ? "Valid BST" : "Invalid BST") << std::endl;

    // 清理分配的内存（注意：在实际应用中，应该使用智能指针来自动管理内存）
    delete root->left;
    delete root->right;
    delete root;

    return 0;
}