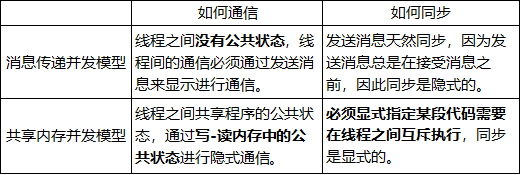
数据表示的最佳方法不仅取决于数据的语义,还取决于所使用的模型种类。线性模型与基于树的模型(比如决策树、梯形提升树、随机森林)是两种成员很多同时又非常常用的模型,他们在处理不同的特征表示时就具有非常不同的性质。
下面是线性回归模型与决策树回归在数据集上的对比:
import mglearn.datasets
from sklearn.linear_model import LinearRegression
from sklearn.tree import DecisionTreeRegressor
import numpy as np
import matplotlib.pyplot as plt
plt.rcParams['font.sans-serif'] = ['SimHei']
plt.rcParams['axes.unicode_minus'] = False
X,y=mglearn.datasets.make_wave(n_samples=100)
line=np.linspace(-3,3,1000,endpoint=False).reshape(-1,1)
reg=DecisionTreeRegressor(min_samples_split=3).fit(X,y)
plt.plot(line,reg.predict(line),label='决策树回归')
reg=LinearRegression().fit(X,y)
plt.plot(line,reg.predict(line),label='线性回归')
plt.plot(X[:,0],y,'o',c='k')
plt.xlabel('输入特征')
plt.ylabel('回归 输出')
plt.show()
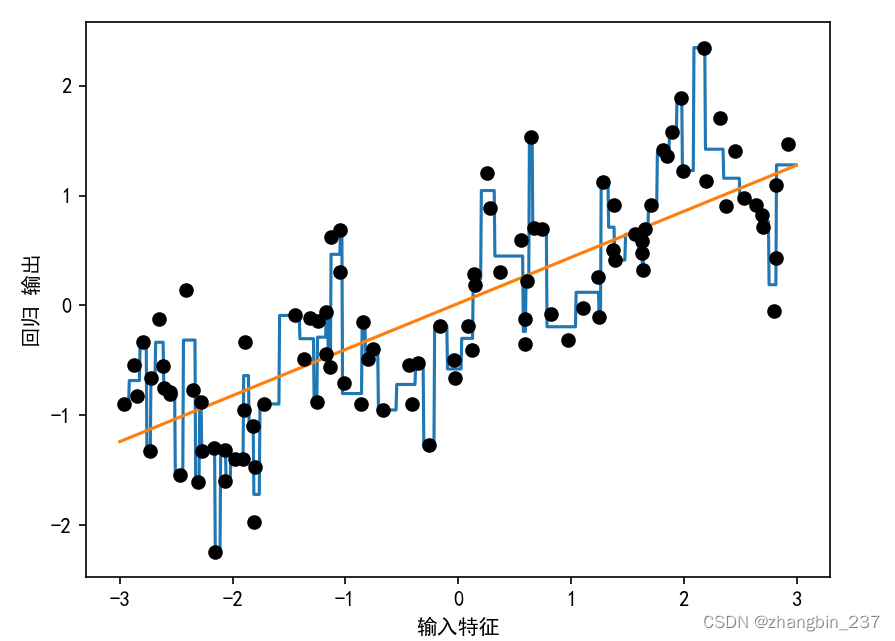
线性模型只能对线性关系建模,对于单个特征的情况就是直线。决策树可以构造更为复杂的数据模型,但这强烈依赖于数据表示。
有一种方法可以让线性模型在连续数据上变得更强大,就是使用特征分箱(也叫离散化)将其划分为多个特征:
我们假设将特征的输入范围划分为固定个数的箱子,比如10个,那么数据点就可以用它所在的箱子来表示。为了确定这一点,我们首先要定义箱子,在这个例子中,我们在-3到3之间定义10个均匀分布的箱子。我们用np.linspace函数创建11个元素,从而创建10个箱子,即两个联系边界之间的空间:
bins=np.linspace(-3,3,11)
print('bins:{}'.format(bins))
在这里,第一个箱子包含特征取值-3到-2.4之间的所有数据点,第二个箱子包含特征取值在-2.4到-1.8之间的所有数据点,以此类推:
which_bin=np.digitize(X,bins=bins)
print('\nData points:\n',X[:5])
print('\nBin membership for data points:\n',which_bin[:5])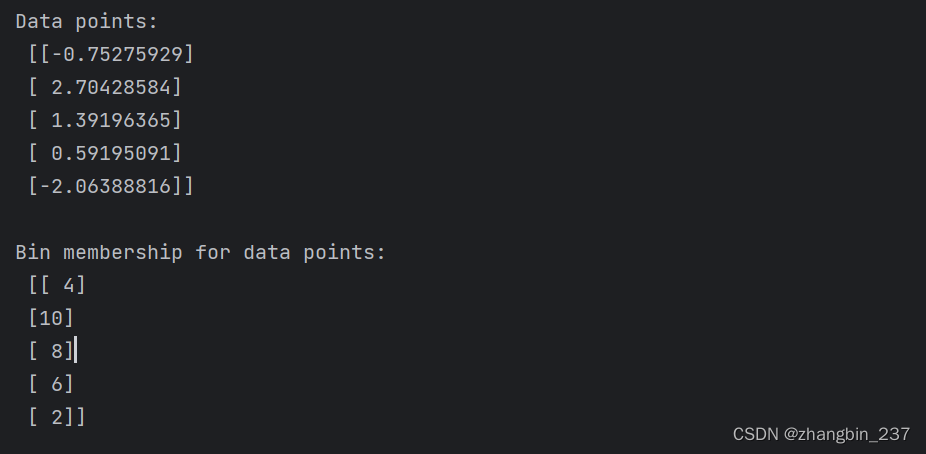
我们在这里做的是将数据集中单个连续输入特征变换为一个分类特征,用于表示数据点所在的箱子。要现在这个数据上使用scikit-learn模型,我们利用preprocessing模块的OneHotEncoder将这个离散特征变换为one-hot编码。
OneHotEncoder实现的编码与pandas.get_dummies相同,但目前它只适用于值为整数的分类变量。
#使用OneHotEncoder进行变换
encoder=OneHotEncoder(sparse=False)
encoder.fit(which_bin)
#transform创建one-hot编码
X_binned=encoder.transform(which_bin)
print(X_binned[:-5])
由于我们指定了10个箱子,所以变换后的X_binned数据集现在包含10个特征:
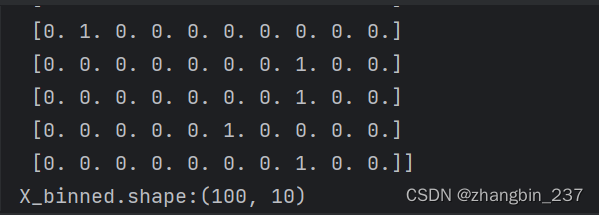
下面我们在one-hot编码后的数据上构建新的线性模型和新的决策树模型:
line_binned=encoder.transform(np.digitize(line,bins=bins))
reg=LinearRegression().fit(X_binned,y)
plt.plot(line,reg.predict(line_binned),label='线性回归')
reg=DecisionTreeRegressor(min_samples_split=3).fit(X_binned,y)
plt.plot(line,reg.predict(line_binned),label='线性回归')
plt.plot(X[:,0],y,'o',c='k')
plt.vlines(bins,-3,3,linewidth=1,alpha=.2)
plt.xlabel('输入特征')
plt.ylabel('回归 输出')
plt.show()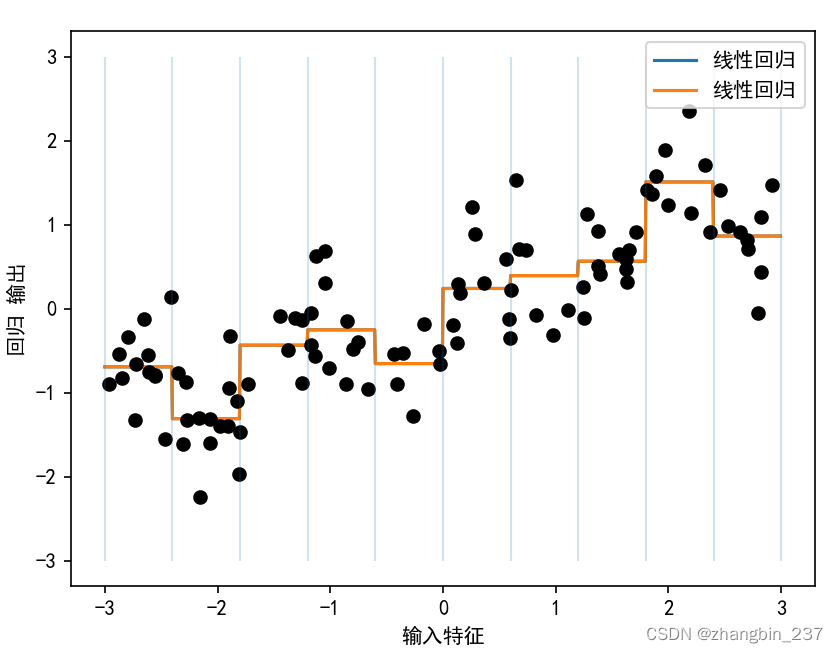
虚线与实线完全重合,说明线性回归模型和决策树做出了完全相同的预测。对于每个箱子,二者都预测一个常数值。因为每个箱子内的特征是不变的,所以对一个箱子内的所有点,任何模型都会预测相同的值。比较对特征进行分箱前后模型学到的内容,我们发现,线性模型变得更加灵活了,因为现在它对每个箱子具有不同的取值,而决策树模型的灵活性降低了。
分箱特征对基于树的模型通常不会产生更好的效果,因为这种模型可以学习在任何位置划分数据。从某种意义上来看,决策树可以学习如何分箱对预测这些数据最为有用。此外,决策树可以同时查看多个特征,而分享通常针对的是单个特征。不过,线性模型的表现力在数据变换后得到了极大的提高。
对于特定的数据集,如果有充分的理由使用线性模型(比如数据集很大、维度很高,但有些特征与输出的关系是非线性的),那么分享是提高建模能力的好方法。