若该文为原创文章,转载请注明原文出处
本文章博客地址:https://hpzwl.blog.csdn.net/article/details/139969415
长沙红胖子Qt(长沙创微智科)博文大全:开发技术集合(包含Qt实用技术、树莓派、三维、OpenCV、OpenGL、ffmpeg、OSG、单片机、软硬结合等等)持续更新中…
硬件相关开发
问题
导入下载的step元器件模型失去3D纹理,基本就等于失去了灵魂了,3D元器件预览失去了最重要的一环,无意发现问题所在,并测试,找到了解决该问题的方法。
原因,可理解为AD21的放置“3D体”BUG
这是标准流程但是Step丢失纹理的导入方法,使用该方法导入ad文件夹中的step也是丢失纹理。
这里是建立的模型本身有纹理的基础上,导入的时候一般选择如下,直接导入3D模型(这里是导入下下来的单独的step模型)。
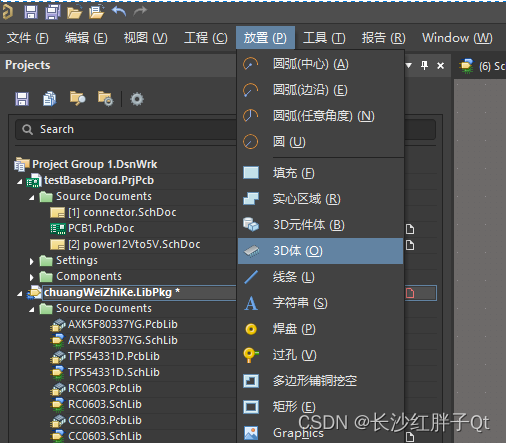
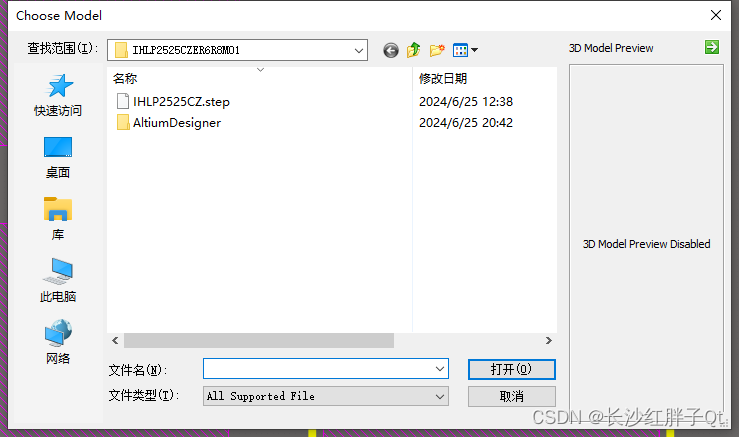


这是放入3D绘图的流程,不丢失纹理的导入方法
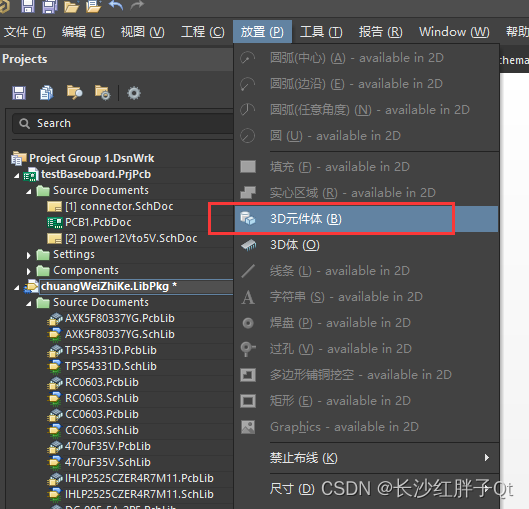
这里时候,看到属性页(右侧),此时鼠标放入属性页还会导致主界面不断移动,先不管,继续:
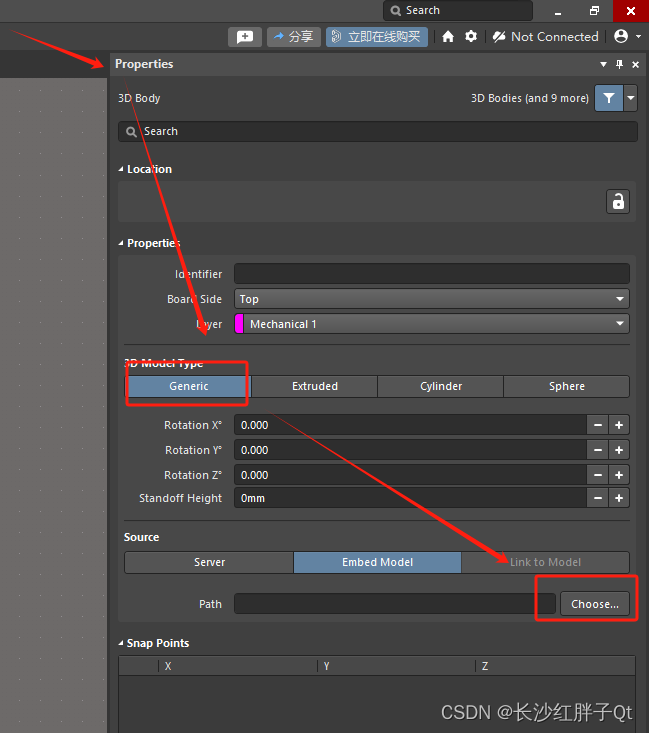
然后赶紧选择导入的step的3D模型文件(这里为了复位可以在视图页面按数字0,可以恢复视图,避免操作久了,视图往右偏移太多,从而找不到元器件了)。
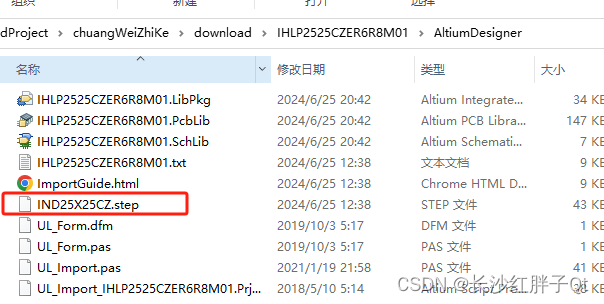
这样才会在其他地方导入step模型复用而有纹理。
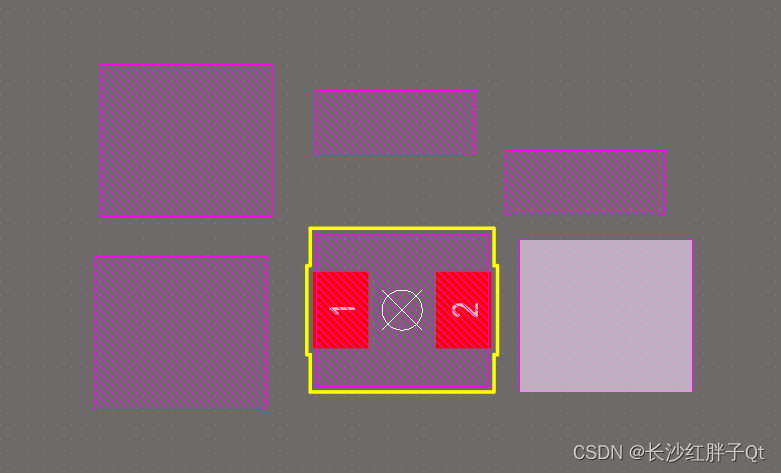
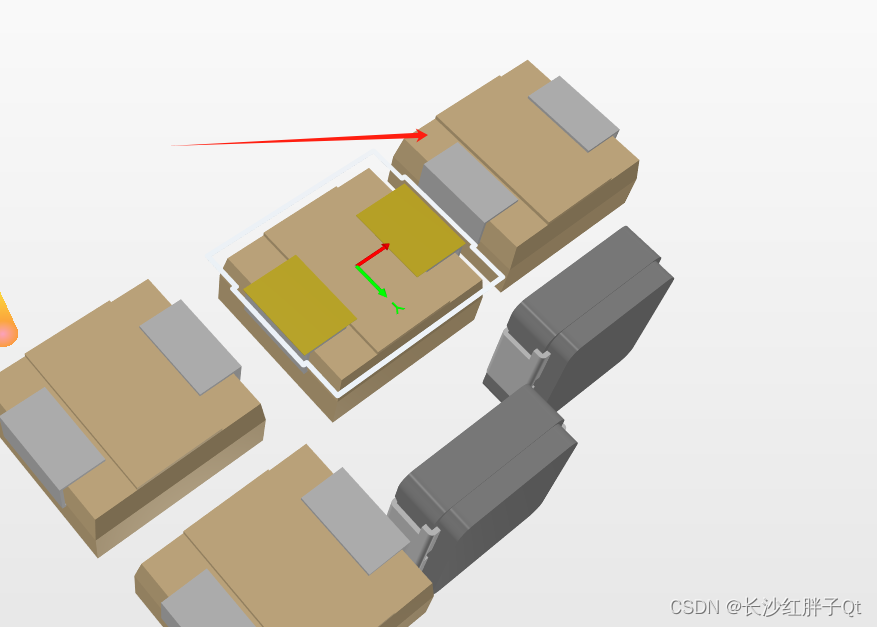
导入一次之后,再使用前面的流程导入这个AD文件夹的step也可以不丢纹理了(使用本方法一次之后,才不会丢)。
再次确认
为了确认,再次导入测试。
"3D体“导入step(有纹理,并不是所有的都是这样没纹理,有些有,原因未知,如果没有则用导入3D元器件的方法):
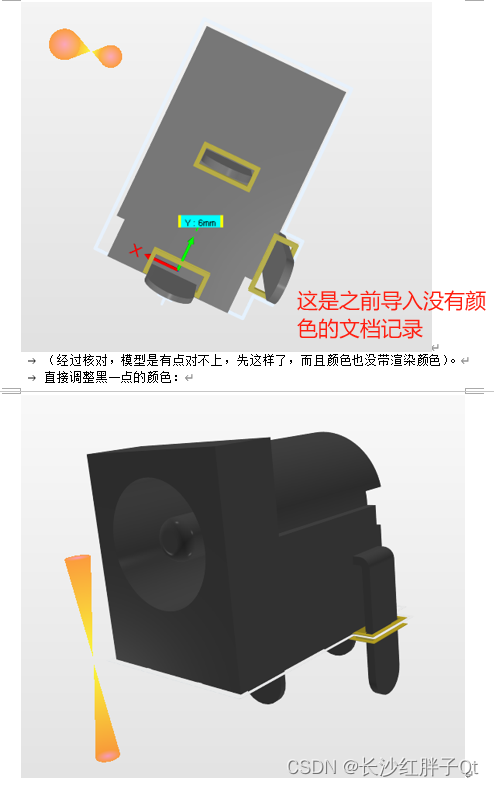

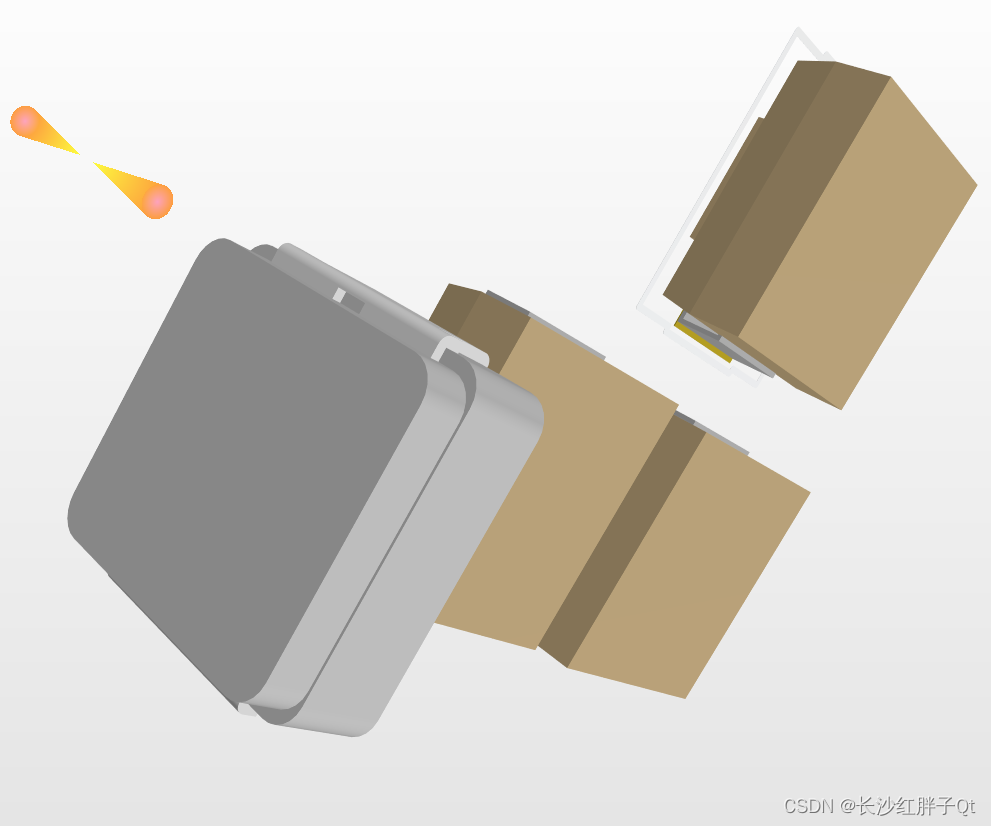
这是之前的板子预览图,突然发现这个问题之后,再导入就有颜色了。
"3D元件体“导入step:

"3D体“导入step:
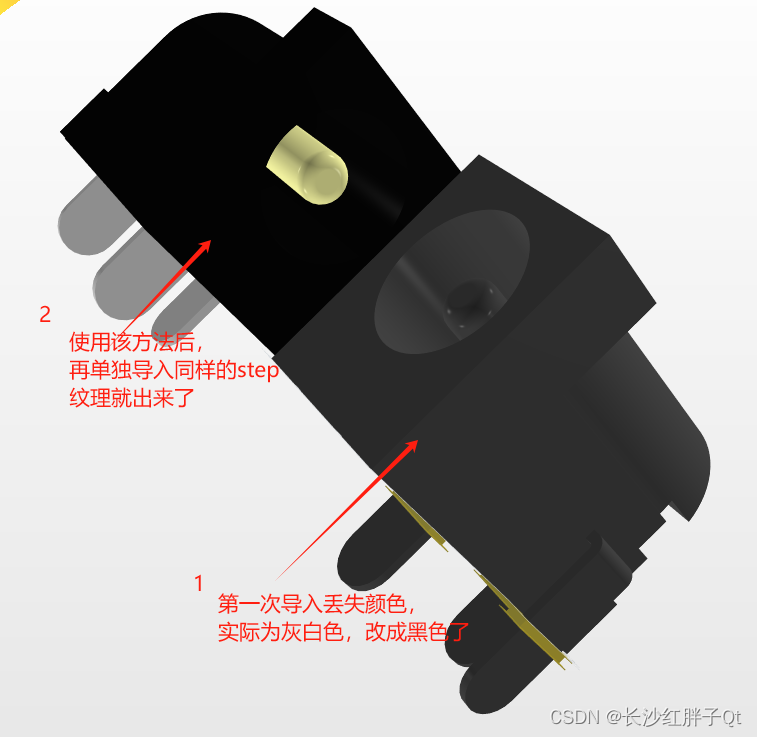
所以这个问题只有第一次产生,如果没有使用”3D元器体“那么一直都是没颜色的,使用一次之后,再次用”3D体“也是有纹理的了,就理解为ad的bug了。
解决方法
如果"3D体“导入没有纹理,那么请私用”3D元器体”导入。
本文章博客地址:https://hpzwl.blog.csdn.net/article/details/139969415