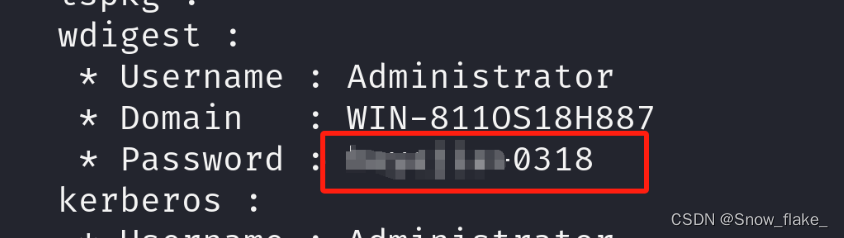
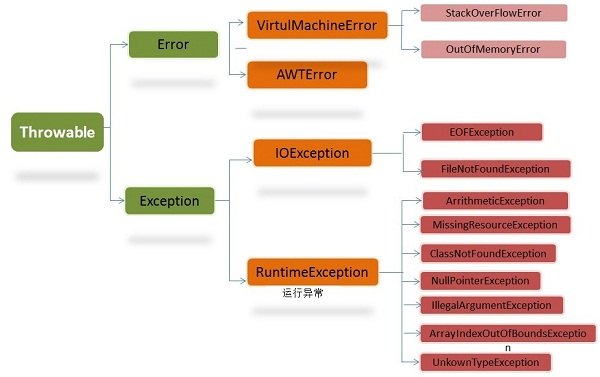
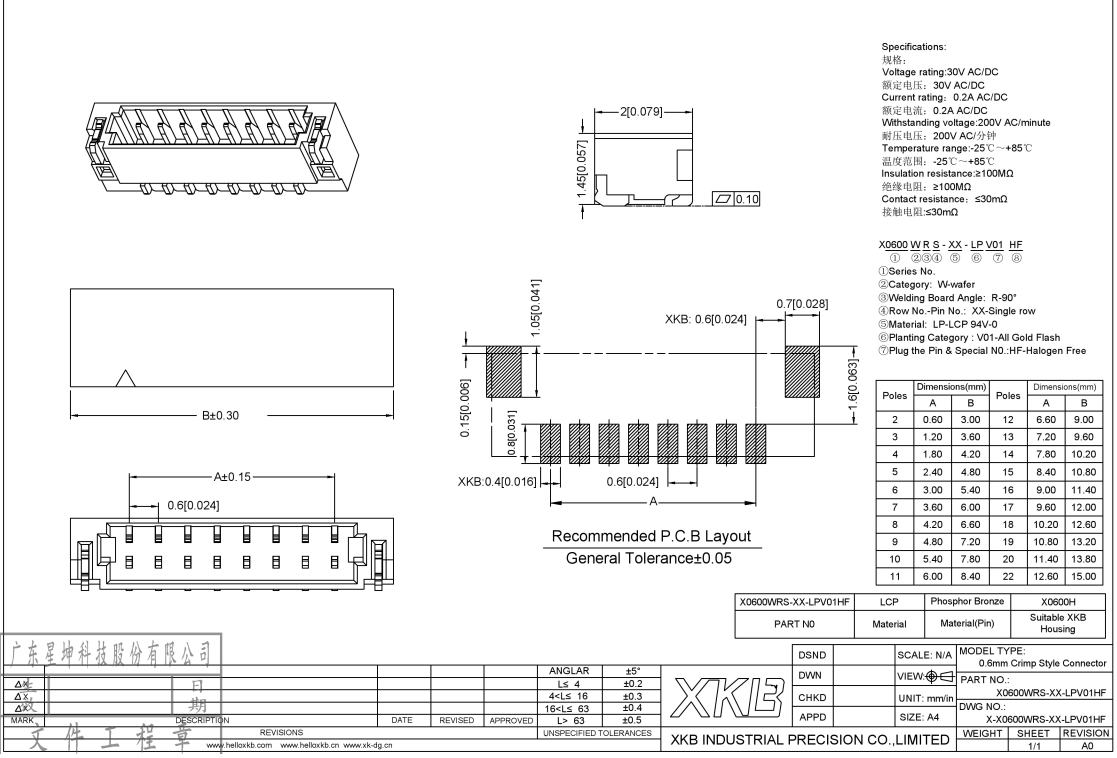
随着科技的不断进步,电子设备在我们的生活和工作中扮演着越来越重要的角色。然而,随之而来的是设备连接的复杂性,这不仅增加了安装和维修的时间成本,还可能因为操作不当而影响设备的性能和寿命。针对这一问题,中国星坤公司推出了X0600系列线对板连接器,旨在通过简化连接过程,提高生产效率,同时降低对专业技能和设备的依赖。

一、X0600系列线对板连接器的特点
X0600系列线对板连接器以其易安装和拆卸的特性,迅速在市场上获得了认可。这种连接器的设计非常人性化,用户无需具备专业的电子知识或使用复杂的工具,仅通过一个普通的插头和插座,就可以轻松实现设备的连接和断开。这种设计大大减少了安装和维修的时间成本,提高了工作效率。
二、应用领域
X0600系列线对板连接器的应用范围非常广泛,它适用于多种电子设备和领域:
1. 液晶屏家电:在电视、显示器等液晶屏家电中,X0600系列连接器可以简化内部线路的连接,提高组装效率。
2. 电动玩具:在电动玩具的生产中,这种连接器可以确保玩具的电路连接既安全又稳定。
3. 数码产品:手机、平板电脑等数码产品的内部连接,通过使用X0600系列连接器,可以提高产品的可靠性和耐用性。
4. 现代办公设备:打印机、扫描仪等办公设备的连接,通过这种连接器,可以简化安装过程,减少维护成本。
5. 通讯设备:在路由器、交换机等通讯设备中,X0600系列连接器有助于提高设备的连接稳定性和传输效率。
6. 特殊电子:在医疗设备、工业控制系统等特殊电子领域,这种连接器可以提供稳定可靠的连接。
7. 笔记本电脑:笔记本电脑的内部连接,使用X0600系列连接器,可以提高组装效率,同时确保连接的稳定性。
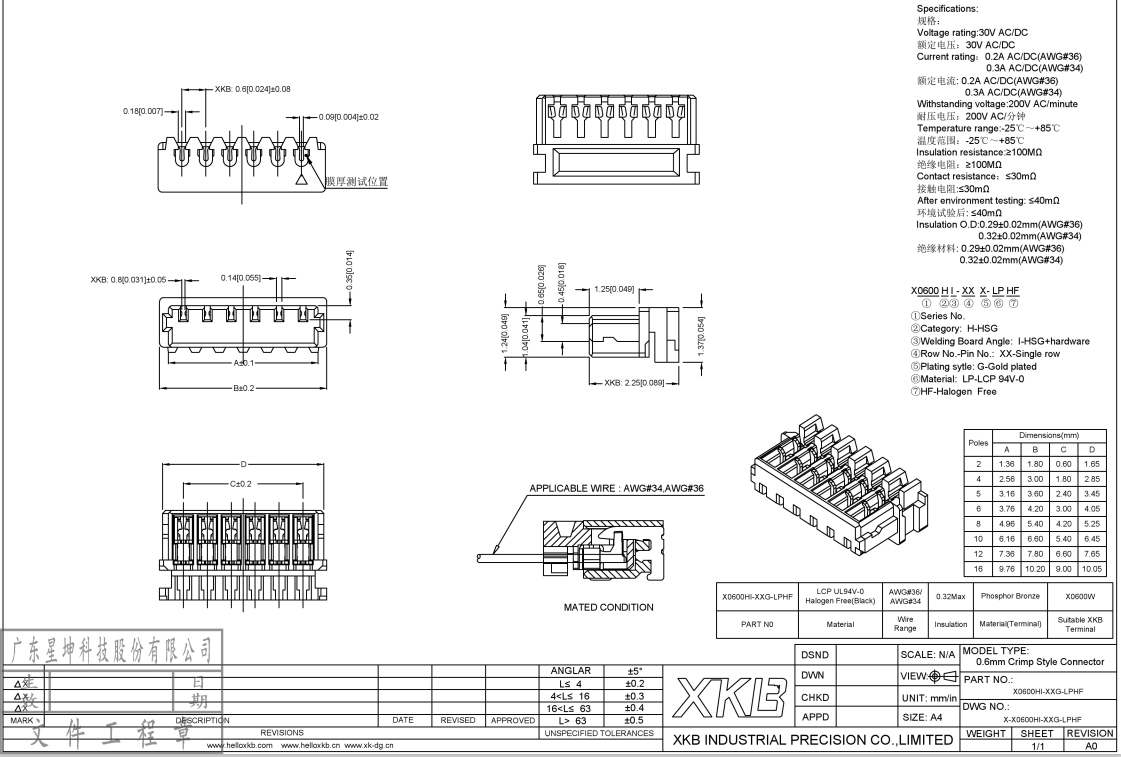
三、技术优势
X0600系列线对板连接器的技术优势主要体现在以下几个方面:
1. 简易操作:用户无需专业技能即可完成连接和断开,大大降低了操作难度。
2. 高兼容性:该连接器设计兼容多种设备,可以适应不同的连接需求。
3. 稳定性:通过精确的工程设计,确保了连接的稳定性,减少了因连接不良导致的设备故障。
4. 耐用性:连接器的材料和制造工艺保证了其长期的耐用性,减少了更换频率。
5. 安全性:设计考虑了电气安全,确保了连接过程中的安全性。

四、市场前景
随着电子设备种类的不断增加和功能的日益复杂化,X0600系列线对板连接器的市场前景十分广阔。它不仅能够满足当前电子设备连接的需求,还能够应对未来技术发展带来的挑战。

中国星坤推出的X0600系列线对板连接器,以其易用性、兼容性、稳定性和安全性,为电子设备的生产和维护提供了一种全新的解决方案。这种连接器的推出,无疑将推动电子行业的进一步发展,为用户带来更加便捷、高效的连接体验。随着技术的不断进步和市场的不断扩大,我们有理由相信,X0600系列线对板连接器将会在未来的电子连接领域占据重要的地位。



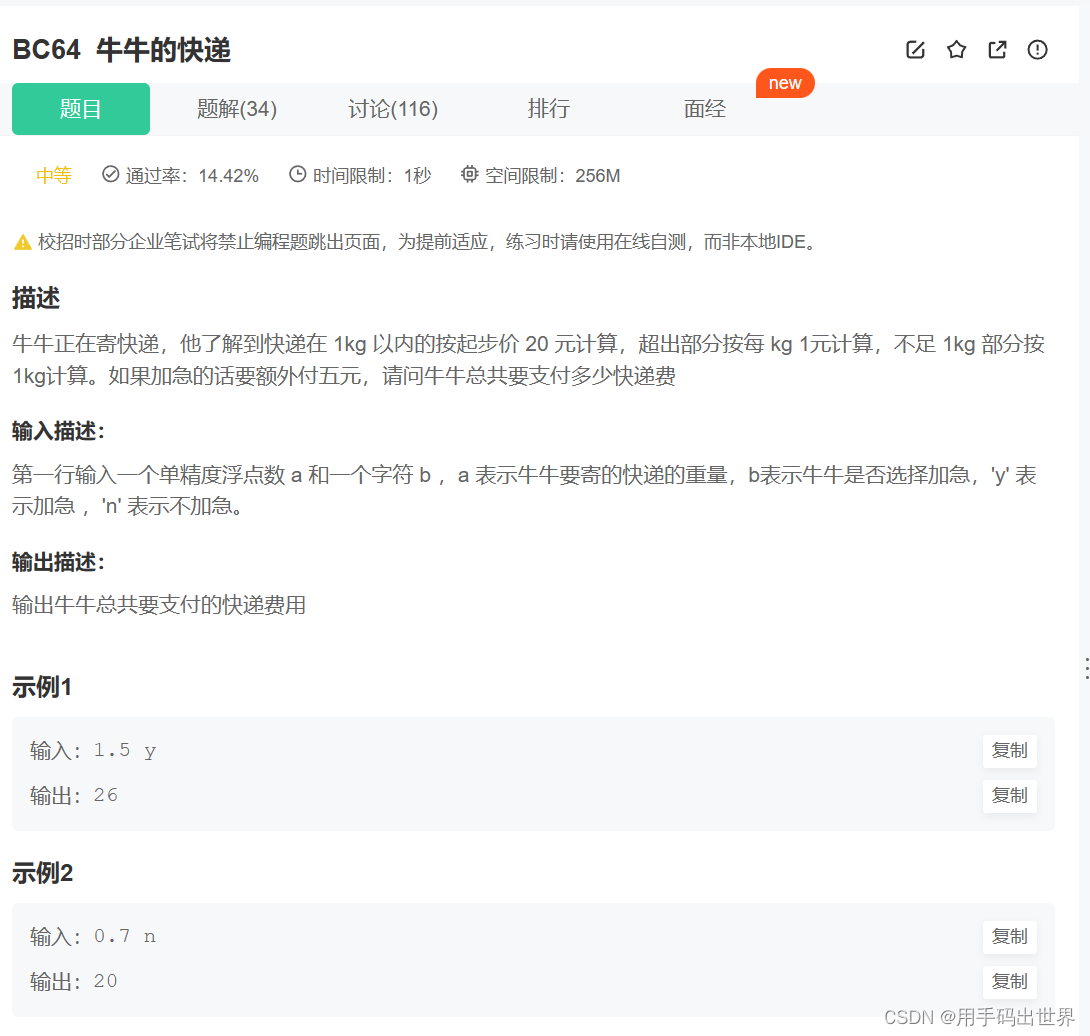
![[leetcode] smallest-k-lcci. 最小的k个数](https://img-blog.csdnimg.cn/direct/dd3f198c82124879b8de82de0902e633.png)