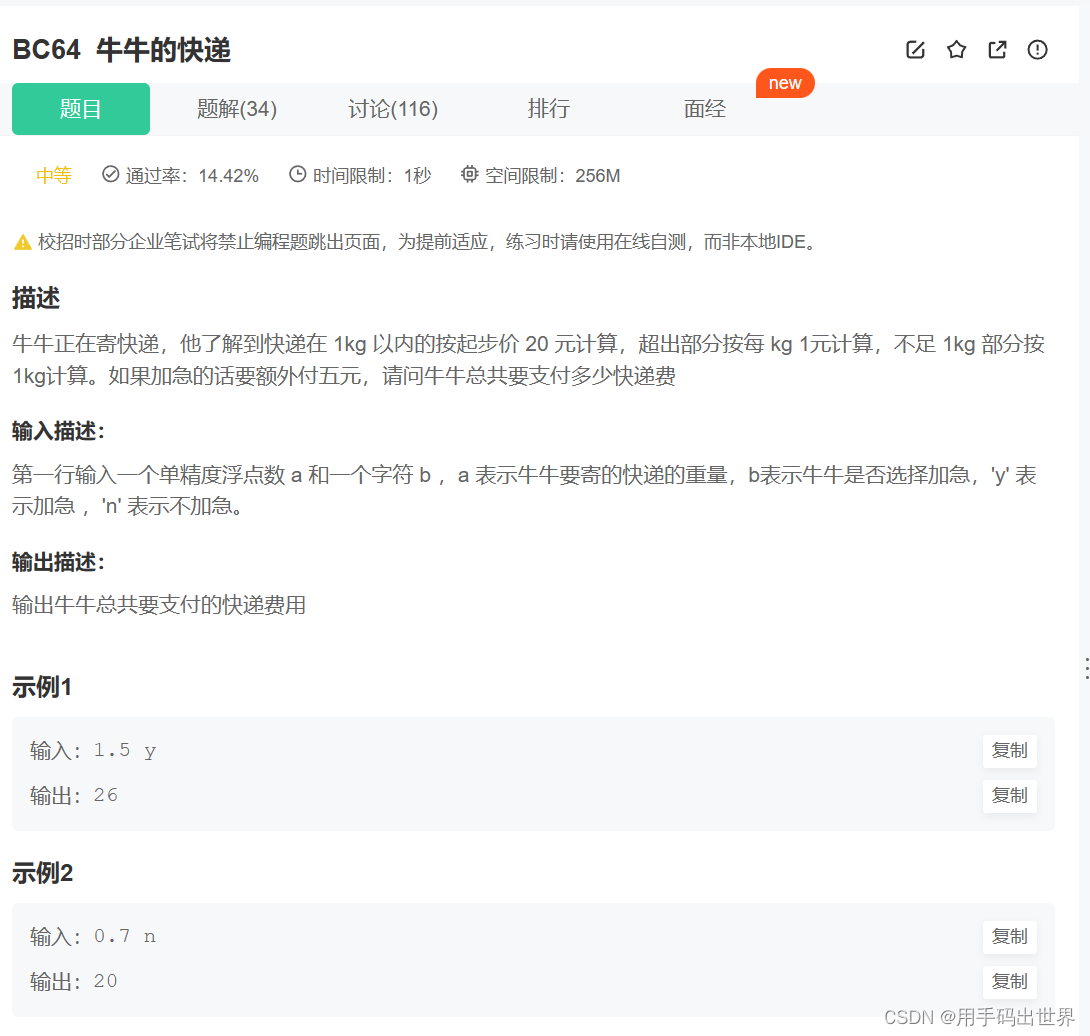
1.图像金字塔

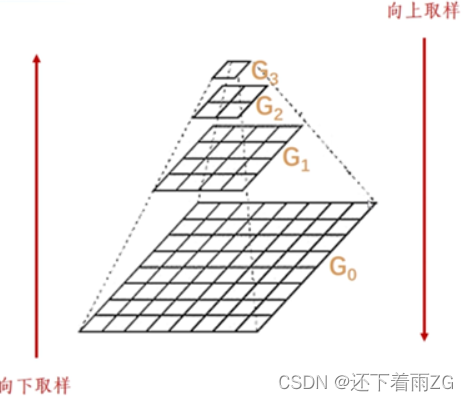
(1)下采样

从G0 -> G1、G2、G3

• step01：对图像Gi进行高斯核卷积操作（高斯滤波）
• step02：删除所有的偶数行和列

void cv::pyrDown(
	cv::Mat &imSrc, //输入图像
	cv::Mat &imDst, //下采样后的输出图像
	cv::Size size = cv::Size(), //imDst的尺寸，默认是输入图像的1、2
	int borderType=4 //一般默认即可
	);

(2)上采样

从G3 -> G2、G1、G0

• step01：将图像在每个方向上扩大为原图像的2倍，新增的行和列均用0来填充
• step02：使用与“向下取样”相同的卷积核乘以4，再与放大后的图像进行卷积运算

void cv::pyrUp(
	cv::Mat &imSrc,
	cv::Mat &imDst,
	cv::Size size=cv::Size(), //默认位imSrc的2
	int borderType = 4
	);

2.高斯金字塔

(1)原理

高斯金字塔的构建就是迭代地对图像进行下采样，下采样的步骤如1中下采样的介绍

(2)How(如何构建高斯金字塔)

构建高斯金字塔函数如下（可直接使用）：

/*@author @还下着雨ZG
 * @param[in] imSrc, 输入的源图像
 * @param[out] vPyrGaussian, 输出的图像金字塔
 * @param[in] iLayer, 金字塔的层数
 * @return int, 正数表示金字塔构建成功，负数表示金字塔构建失败
*/
int GetPyrGaussian(const cv::Mat &imSrc, std::vector<cv::Mat>& vPyrGaussian,int iLayer)
{
    if (imSrc.empty())
        return -1;
    if (!vPyrGaussian.empty())
    {
        vPyrGaussian.clear();
    }
    if (iLayer <= 0)
        return -2;
    //下采样
    vPyrGaussian.resize(iLayer);
    cv::Mat imTmp;
    for (int i = 0; i < iLayer; ++i)
    {
        if (i == 0)
            vPyrGaussian[i] = imSrc;
        else {
            cv::pyrDown(vPyrGaussian[i-1], imTmp);
            vPyrGaussian[i] = imTmp;
        }
    }
    return 1;
}

3拉普拉斯图像金字塔

(1)What(什么是拉普拉斯图)

拉普拉斯图是基于高斯图的，拉普拉斯图的本质是残差，即第i层的高斯图 - 先缩小后放大的图；不明白可直接看下面构建拉普拉斯图像金字塔函数。

(2)How(如何构建拉普拉斯图像金字塔)

构建拉普拉是图像金字塔，可直接使用：

/*@author @还下着雨ZG
 * @param[in] vPyrGaussian, 输入的高斯图像金字塔
 * @param[out] vPyrLaplacian, 输出的拉普拉斯图像金字塔
 * @return int, 正数表示金字塔构建成功，负数表示金字塔构建失败
*/
int GetPyrLaplacian(const std::vector<cv::Mat>& vPyrGaussian,std::vector<cv::Mat>& vPyrLaplacian)
{
    /*对输入参数及其约束关系进行检查*/
    if (vPyrGaussian.empty())
        return -1;
    if (!vPyrLaplacian.empty())
        vPyrLaplacian.clear();

    /*构建拉普拉斯金字塔*/
    cv::Mat imLplTmp;
    for (int i = 0; i < vPyrGaussian.size()-1; ++i)
    {
        cv::Mat imTmp(vPyrGaussian[i].size(), vPyrGaussian[i].type());
        cv::pyrUp(vPyrGaussian[i + 1], imTmp);
        imLplTmp = vPyrGaussian[i] - imTmp;
        vPyrLaplacian.push_back(imLplTmp);
    }
    return 1;
}

(3)使用opencv自带的函数获取拉普拉斯图像

void cv::Laplacian(
	cv::Mat &imSrc, //输入图像
	cv::Mat &imLpl, //输出的拉普拉斯图像
	int ddepth, //imLpl的数据格式
	int ksize =1, 
	double scale=1, //拉普拉斯值的缩放值
	double delta = 0, //偏置值
	int borderType = BORDER_DEFAULT
	);