目录
1、题目链接
2、题目分析
1.状态表示
2.状态转移方程
3.初始化
4.填表
5.返回值
3、代码解析
1、题目链接
123. 买卖股票的最佳时机 III

2、题目分析
1.状态表示
由题目可知,我们分为两种状态,买入和卖出,又因为只能完成两次交易,我们可以画图分析:
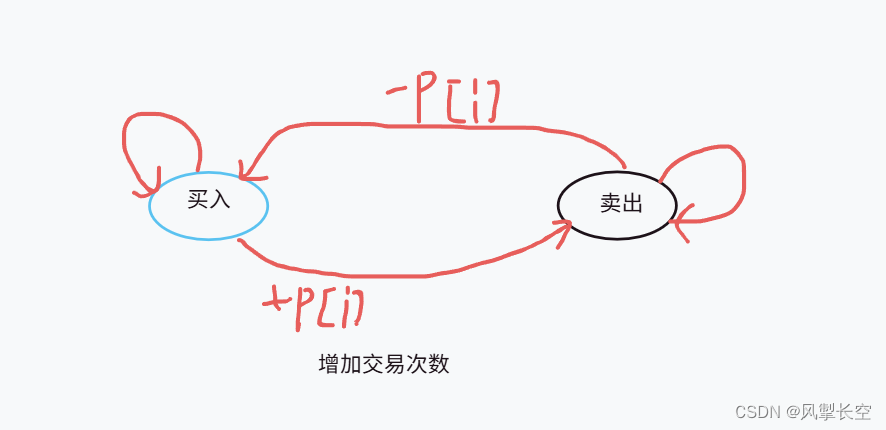
可以看出,从买入到买入,也可以从买入到卖出;
从卖出到卖出,也可以从卖出到买入,但是会增加交易次数;
所以我们用
f[i][j]表示第i天,交易j次后,处于买入状态的最大利润
g[i][j]表示第i天,交易j次后,处于卖出状态的最大利润
2.状态转移方程
由图分析:
f[i][j] = max(f[i - 1][j], g[i - 1][j] - prices[i]);
g[i][j] = max(g[i-1][j], f[i - 1][j - 1] + prices[i]);
关于第二个状态转移方程,如果j=0,那么就会有报错的风险,怎么解决呢?
加个if判断就好了
g[i][j] = g[i - 1][j];
if (j >= 1) // 如果该状态存在
g[i][j] = max(g[i][j], f[i - 1][j - 1] + prices[i]);
只有当j>=1的时候,才执行 g[i][j] = max(g[i][j], f[i - 1][j - 1] + prices[i]),就可以解决这个问题了;
3.初始化
在第0天,交易0次,处于买入的状态下,最大利润是f[0][0]=-p[0];
在第0天,交易0次,处于卖出的状态下,最大利润是g[0][0]=0;
注意,在第0天,是不可能出现交易一次或者交易两次的情况的,所以f[0][1]和f[0][2]是取不到的,所以我们将它设置为无穷小;这可以确保我们后面的计算是正确的;
还要注意,我们设置无穷小和无穷大时,和其他数计算会发生溢出的风险,所以为我们取int最大值的一半0x3f3f3f3f(十六进制),这样这个值既可以足够小,又不会有溢出的风险;
4.填表
按照从上到下,从左到右的顺序填表
5.返回值
我们需要返回的是在最后一天得到的最大的利润,但是不知道交易了几次,所以,我们要求出最后一天的利润的最大值
3、代码解析
int maxProfit(vector<int>& prices) {
int n = prices.size();
const int INT = 0x3f3f3f3f;
vector<vector<int>> f(n, vector<int>(3, -INT));
auto g = f;
// 初始化
f[0][0] = -prices[0], g[0][0] = 0;
// 状态转移方程
// f[i][j]表示第i天,交易j次后,处于买入状态的最大利润
// g[i][j]表示第i天,交易j次后,处于卖出状态的最大利润
for (int i = 1; i < n; i++) {
for (int j = 0; j < 3; j++) {
f[i][j] = max(f[i - 1][j], g[i - 1][j] - prices[i]);
g[i][j] = g[i - 1][j];
if (j >= 1) // 如果该状态存在
g[i][j] = max(g[i][j], f[i - 1][j - 1] + prices[i]);
}
}
int ret = 0;
for (int i = 0; i < 3; i++) {
ret = max(ret, g[n - 1][i]);
}
return ret;