Welcome to 9ilk's Code World

(๑•́ ₃ •̀๑) 个人主页: 9ilk
(๑•́ ₃ •̀๑) 文章专栏: 算法Journey
本篇博客我们将介绍关于字符串匹配的BF算法以及KMP算法,请放心食用~
🏠 字符串匹配
假设有一个字符串为主串str,另一个字符串为子串sub,我们需要在str中找到sub出现的第一个位置,没有就返回-1表示找不到。
eg : str = “abcde” sub = “bcd” ---> 子串在主串第一次出现的位置是1
🏠 BF算法
BF算法也叫做“暴力匹配算法”,也就是在主串固定一个左端点left,定义一个右端点right,right一开始在left位置,让right遍历一次主串,子串也用一个变量cur遍历,没找到匹配的让left向前移动一位,cur回退到子串起始位置,right回退到新left位置再次遍历,直到left找到匹配的子串或者找不到的情况。
动画展示:
注意点:
- 当子串为空串时没必要此时表示没找到
- 当子串大于主串时无法进行匹配
- 当开始匹配的位置不合理时无法进行匹配
- 结束条件 : cur走完了子串找到了 / left走完了主串但cur没走完表示没走到
参考代码:
//BF算法
int BF(string & str, string& sub,int pos = 0)
{
//判断位置合法性 以及主串子串合法性
int lenstr = str.size();
int lensub = sub.size();
if (lensub > lenstr || lensub == 0)
return -1;
if (pos < 0 || pos >= lenstr)
return -1;
int left = pos;
int right = left; //遍历主串
int cur = 0;
while (cur < lensub && left < lenstr)
{
if (str[right] == sub[cur])
{
cur++;
right++;
}
else
{
cur = 0;
left++;
right = left;
}
}
//终止条件
if (cur >= lensub)
{
return left;
}
return -1;
}时间复杂度 : O(m*n) m为主串长度,n为子串长度
🏠 KMP算法
📒 引入

在了解完BF算法后,对于此时的不匹配,我们很自然的会想要把left向前挪,再从头逐个比较。这样做虽然可行,但是效率很差,因为你要把"搜索位置"移到已经比较过的位置,重比一遍。

那有什么改进效率的方法呢?
📒 什么是KMP
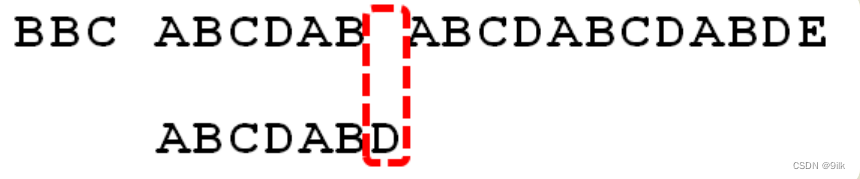
对于此时不匹配我们能提取到的一个信息是你其实知道前面六个字符是"ABCDAB",因此我们可以利用这个信息找到最大程度能匹配子串的一部分,此时就是最好的情况
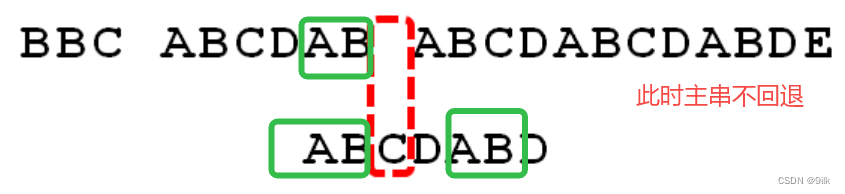
这便是KMP算法的核心 --- 利用匹配失败后的信息,尽量减少模式串与主串的匹配次数以达到快速匹配的目的。与BF算法不同的是,当匹配失败时,主串时不回退的,子串回退到相应位置。
问题是KMP算法中,当匹配失败时,子串怎么知道该回退到哪个位置?
📒 next数组
所谓next数组,保存的是子串中某个位置匹配失败后应该回退到的位置
- 规律1
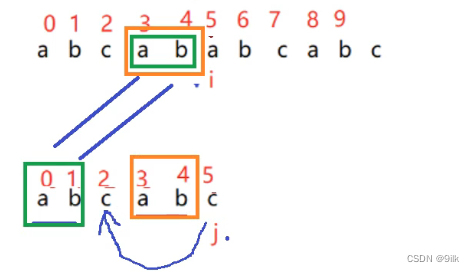
对于这对字符串匹配,当在i位置匹配失败时,为了能够在主串中尽量找到和子串匹配的一部分,此时j最好回退到2号下标,而我们发现子串中[0,1]和[3,4]这两个相同的部分长度正好是2
因此找j所要回退的位置关键是去找在主串匹配成功的部分里面取去找到一部分子串1(比如上面子串的【3,4】)和我们子串里面一部分串是相同的(比如子串里面的【0,1】和【3,4】)
✏️ 手动求next数组
next数组:next[j]=k;,不同的j来对应一个K值,这个K就是你将来要移动的j要移动的位置。
1、规则:找到匹配成功部分的两个相等的真子串(不包含本身),一个个以下标0开始,另一个以j-1下标结尾。
2、不管什么数据next[0]=-1;next[1]=0;在这里,我们以下标来开始,而说到的第几个第几个是从1开始;
示例1 :
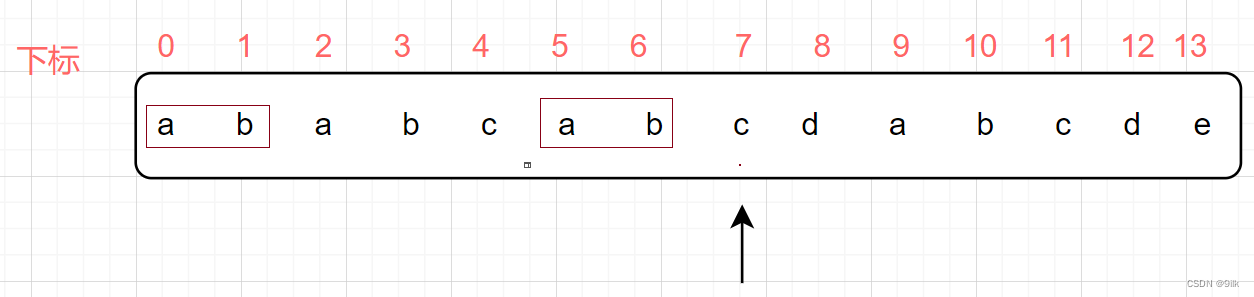
对于下标7的位置,它前面对应的【0,1】和【5,6】区间是两个相等的真子串,因此当在7下标匹配失败时,j应该回退到2号位置,也就是next[7] = 2;
示例2 :
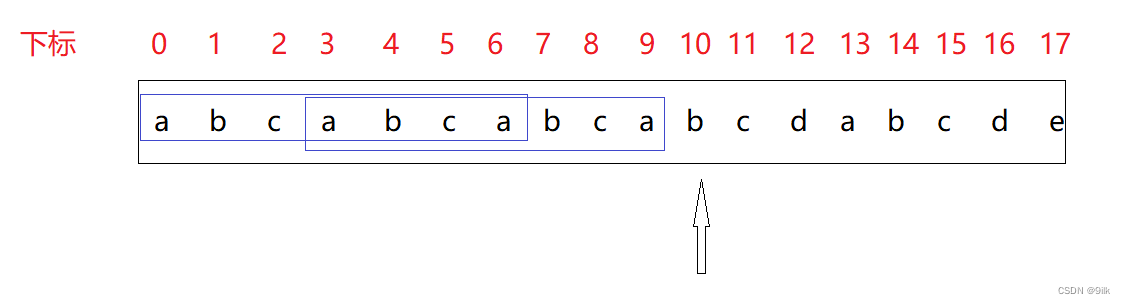
对于下标10的位置,它前面【0,6】和【3,9】区间是两个相等的真子串,因此此时next[10] = 7;
练习:
- 对于"ababcabcdabcde",求其的next数组?
- 再对"abcabcabcabcdabcde",求其的next数组?"
答案 :
1. -10012012001200
2. -100012345678901230
小tips : 每个next数组中next[i+1]如果是大于next[i],一定有next[i + 1] = next [i] + 1;
✏️ 已知next[i] 如何求 next[i+1]
前提 : 假设 next [ i ] = k;
- p[i] = p[k]时(比如下面字符串中下标8对应字符等于下标3对应字符)
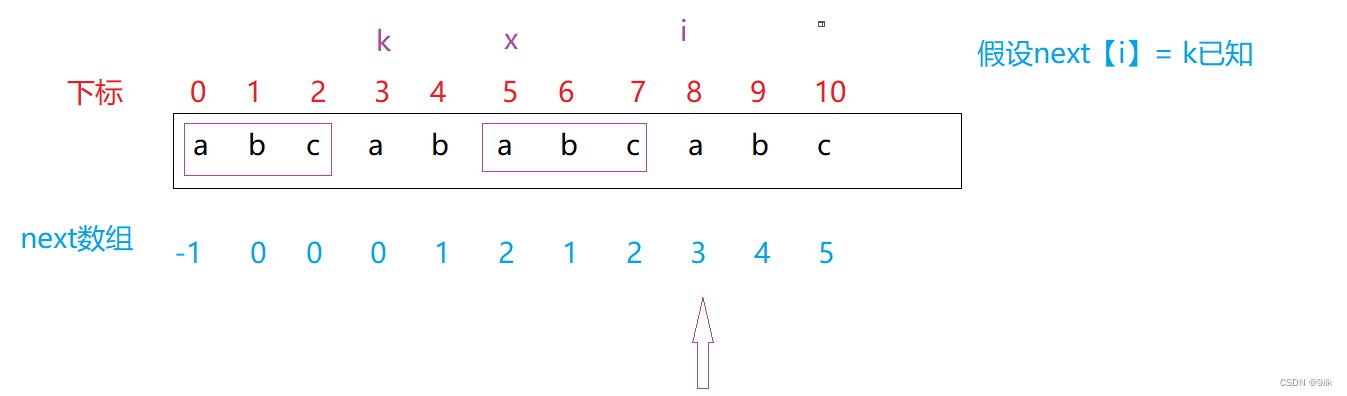
我们假设x为第二个真子串起始位置,注意x的位置不一定就是k
因此我们可以得到 k - 1 - 0 = i - 1 - x;
--> x = i - k; k = i - x;
--->p[0]...p[x] == p[0]...p[k-1] == p[i-k]...p[i-1] (1)
又由于 p[i] == p[k] (2)
由(1)(2)式得 : p[0]...p[k-1][k] == p[i-k]...p[i-1]p[i]
---> p[0]...p[k] == p[i-k]...p[i] (3)
由数学归纳法可知: next[i] = k 对应 (1)式,同理next[i+1] = k + 1对应(3)式
- p[i] != p[k]
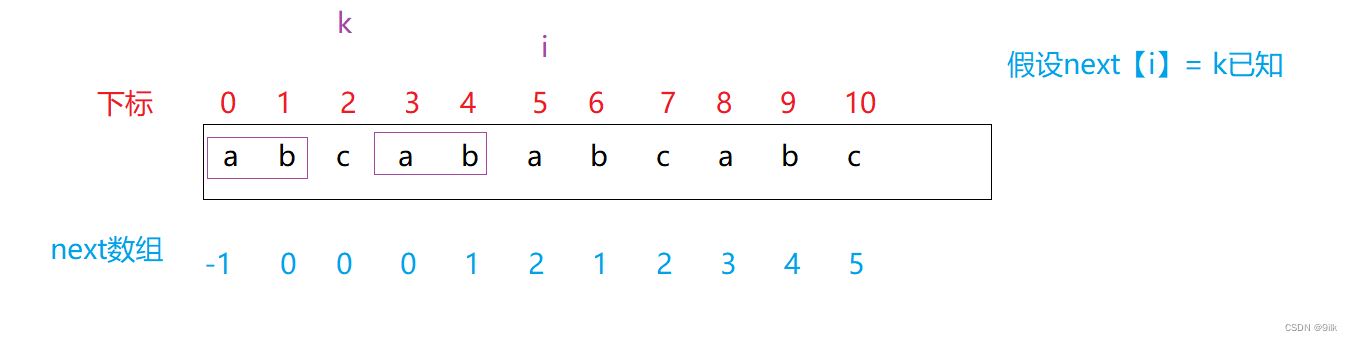
我们可以发现此时next[i+1] != k+1 ,也就是k回退到的2号位置不是你需要的,那怎么办呢?此时我们需要继续回退到2号对应next数组的值,此时k回退到了0下标且此时p[i] = p[k],k+1正好等于next[i+1],即next[6]
因此 如果p[i] != p[k] ,此时我们需要一直回退,回退到满足p[i] == p[k]的情况.
📒 简单实现KMP算法
- 获得next数组
整体思路是基于我们推导的next[i] 求 next[i+1]分为p[i] == p[k] 和 p[i] != p[k]两种情况,由于下标0和1我们已知(规定了是-1和0,next[0] = -1,next[1] = 0),因此我们在求next[2]时我们可以利用next[1],同理next[3]可以利用next[2]... 因此我们next[i]的求法就是去利用next[i-1].
注: 当p[i] != p[k]时,我们的k可能一直回退到-1此时我们把他归类到p[i] == p[k]的情况直接让此时的next[i] = k + 1;
参考代码 :
void GetNext(vector<int>& next,string& sub)
{
if (sub.size() >= 1)
{
next[0] = -1;
}
next[1] = 0;
int k = 0;//指的是前一项的k
int i = 2; //从下标为2开始
while (i < sub.size())
{
if (k == -1 || (sub[i - 1] == sub[k])) // p [i] == p [k]
{
next[i] = k + 1;
i++;
k++;
}
else
{
k = next[k]; // p[i] != p[k] 回退到满足 p[i] == p[k]
}
}
}- KMP算法整体逻辑
核心步骤:
1. 获取next数组
2. 匹配失败时,根据next数组的信息快速匹配
⚠️:主串和子串和合法性以及开始匹配位置的合法性
参考代码:
int KMP(string& str, string& sub, int pos = 0)
{
int lenstr = str.size();
int lensub = sub.size();
if (pos < 0 || pos >= lenstr)
return -1;
if (lensub > lenstr || lensub == 0)
return -1;
int i = pos; //遍历主串
int j = 0; // 遍历子串
//获取next数组
vector<int> next;
next.resize(lensub);
GetNext(next,sub);
while (i < lenstr && j < lensub)
{
if (j == -1 || str[i] == sub[j]) // 注意j可能根据匹配信息回退到-1
{
i++;
j++;
}
else
{
j = next[j]; //匹配失败要回退的位置
}
}
if (j >= lensub)
return i - j;
else
return -1;
}
本博客主要是简单的科普字符串算法,文章设计的数学知识可能不严谨欢迎指正!








![[JS]对象](https://img-blog.csdnimg.cn/img_convert/d11c90b3175d4a4d3bb29625a244659a.png)