• easy-rl PDF版本 笔记整理 P3
• joyrl 比对 补充 P4 - P5
• 相关 代码 整理 ——> 有空 另开一页

最新版PDF下载
地址：https://github.com/datawhalechina/easy-rl/releases
国内地址(推荐国内读者使用)：
链接: https://pan.baidu.com/s/1isqQnpVRWbb3yh83Vs0kbw 提取码: us6a

easy-rl 在线版本链接 (用于 copy 代码)
参考链接 2：https://datawhalechina.github.io/joyrl-book/

其它：
【勘误记录 链接】
——————
5、深度强化学习基础 ⭐️
开源内容：https://linklearner.com/learn/summary/11
——————————

表格型：蒙特卡洛、Q-learning、Sarsa

状态转移概率 $p[s_{t+1},r_t|s_t,a_t]$： 在状态 $s_t$ 选择动作 $a_t$ 后， 转移到状态 $s_{t+1}$，得到奖励 $r_t$ 的概率。

马尔可夫性质： 系统下一时刻的状态仅由当前时刻的状态决定， 不依赖于以往任何状态。

状态转移概率 和 奖励未知： model-free。 免模型

模型未知 或 模型太大 ——> 免模型方法

考虑未来的总奖励的原因： 奖励延迟

折扣因子 $\gamma$： 当前行为 对 太远的未来的某一个回报可能毫无关系。

用下一状态的价值 来更新 当前状态的 价值。 自举
时序差分： 每走一步更新一次 Q 表格， 用下一个状态的 Q 值 来 更新当前状态 的 Q 值。

蒙特卡洛方法：
采样大量 episode ，计算所有 episode 的真实回报，计算平均值， 当做 状态值的估计。

蒙特卡洛：
$V(s_t)\leftarrow V(s_t)+\alpha (G_{i,t}-V(s_t))$

时序差分：
$V(s_t)\leftarrow V(s_t)+\alpha (r_{t+1}+\gamma V(s_{t+1})-V(s_t))$

时序差分	蒙特卡洛
可在线学习，效率高	必须等游戏结束
不要求序列完整	完整序列
连续任务	有终止的任务
马尔可夫	非马尔可夫更高效
有偏估计	无偏估计
方差小、自举	方差大

时序差分 优势： 低方差， 能够在线学习， 能够从不完整的序列中学习。

————————————————

证明：对于任意 策略 $\pi$， 根据其动作价值函数 $q_{\pi }$ 计算的 $\epsilon$ -贪心策略 ${\pi }^{\prime }$ 比原策略 $\pi$ 好 或 至少一样好。

$$\pi (a|s)=\{\begin{array}{rlr}& \frac{\epsilon }{|\mathcal{A}(s)|}+1-\epsilon ,& 贪心动作\\ & \frac{\epsilon }{|\mathcal{A}(s)|},& 其它动作\end{array}$$

由上式：
——>$$\pi (a|s)-\frac{\epsilon }{|\mathcal{A}(s)|}=\{\begin{array}{rlr}& 1-\epsilon ,& 贪心动作\\ & 0,& 其它动作\end{array}$$
——> $$\frac{\pi (a|s)-\frac{\epsilon }{|\mathcal{A}(s)|}}{1-\epsilon }=\{\begin{array}{rlr}& 1,& 贪心动作\\ & 0,& 其它动作\end{array}$$

$\begin{array}{rl}{q}_{\pi }(s,{\pi }^{\prime }(s))& =\sum _{a\in \mathcal{A}}{\pi }^{\prime }(a|s)q_{{\pi }^{\prime }}(s,a)\\ & =\frac{\epsilon }{|\mathcal{A}(s)|}\sum _{a\in \mathcal{A}}{q}_{\pi }(s,a)+(1-\epsilon )\underset{a\in \mathcal{A}}{\max }{q}_{\pi }(s,a)\\ & =\frac{\epsilon }{|\mathcal{A}(s)|}\sum _{a\in \mathcal{A}}{q}_{\pi }(s,a)+(1-\epsilon )\sum _{a\in \mathcal{A}}\frac{\pi (a|s)-\frac{\epsilon }{|\mathcal{A}(s)|}}{1-\epsilon }\underset{a\in \mathcal{A}}{\max }{q}_{\pi }(s,a)\\ & \ge \frac{\epsilon }{|\mathcal{A}(s)|}\sum _{a\in \mathcal{A}}{q}_{\pi }(s,a)+(1-\epsilon )\sum _{a\in \mathcal{A}}\frac{\pi (a|s)-\frac{\epsilon }{|\mathcal{A}(s)|}}{1-\epsilon }{q}_{\pi }(s,a)这个q_{\pi }(s,a)没有\epsilon 贪心动作对应的q大\\ & =\sum _{a\in \mathcal{A}}\pi (a|s)q_{\pi }(s,a)\end{array}$

————————————

偏差高： 偏离真实数据
方差高： 数据分布分散。

时序差分： 更新 V
Sarsa：更新 Q
$$q(s_t,a_t)=q(s_t,a_t)+\alpha [\underset{时序差分误差}{\underbrace{\stackrel{时序差分目标}{\overbrace{r_{t+1}+\gamma q(s_{t+1},a_{t+1})}}-q(s_t,a_t)}}]$$

Sarsa： $(s_t,a_t,r_{t+1},s_{t+1},a_{t+1})$

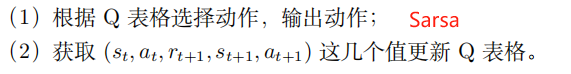
Sarsa： 同策略的时序差分
Q-learning： 异策略的时序差分

$$q(s_t,a_t)=q(s_t,a_t)+\alpha [\underset{时序差分误差}{\underbrace{\stackrel{时序差分目标}{\overbrace{r_{t+1}+\gamma \underset{a}{\max }q(s_{t+1},a)}}-q(s_t,a_t)}}]$$

同策略：学习的策略 和 与环境交互的策略 是同一个。不稳定、胆小。 Sarsa
异策略：目标策略 和 行为策略。 激进。 Q-learning

————————
Q 表格： 横轴 动作， 纵轴 状态

同策略 VS 异策略： 生成样本的策略 和 参数更新的策略 是否相同。

Q 学习， 异策略， 优化策略 没有用到 行为策略的数据。

时序差分 使用了 自举， 实现了 基于平滑的效果， 方差较小。

——————————————
joyrl

免模型：
不需要学习较为复杂的模型 (状态转移概率 和 奖励)
需要与真实环境进行大量的交互。

异策略算法：从经验池或者历史数据中进行学习的。

其一是智能体在测试的时候直接用模型预测的动作输出就行，即在训练中是采样动作（带探索），测试中就是预测动作，其二是训练过程中不需要更新策略，因为已经收敛了。