简介

机器人动力学是对机器人机构的力和运动之间关系与平衡进行研究的学科。机器人动力学是以机器人运动为基础，研究在运动过程中连杆与连杆之间、连杆与工件之间力或力矩等关系。

分类： 根据研究方向的不同，机器人的动力学分析也分为正、逆两个方向。

1. 正动力学问题。根据关节驱动力矩或力，求解关节变量在关节空间的轨迹或末端执行器在笛卡尔空间的轨迹。

2. 逆动力学问题。机器人在关节变量空间的轨迹已确定，或末端执行器在笛卡尔空间的轨迹已确定（轨迹已被规划），求解机器人在各执行器的驱动力或力矩。

建模方法

对于大多数的工业关节型机器人而言，至少具有两个或者两个以上的自由度，其动力学系统形式则为多输入多输出的复杂系统，存在严重的非线性，目前在推导建立机器人动力学方程的过程中，分析机器人的动力学数学模型有很多种方法，第一种方法基于Lagrange Formulation（拉格朗日方程），第二种方法基于Newton-Euler Formulation（牛顿-欧拉方程），此外还有Kane（凯恩法）和Spatial Operator Algebra（空间算子代数）等方法。

动力学建模目的

1. 对于正向动力学问题，其分析是进行机器人仿真的基础；
2. 逆向动力学问题是为了实时控制的需要，利用动力学模型、实现最优控制、以期达到良好的动态性能和最优指标。
3. 在进行机器人结构设计时，需要根据连杆质量、运动学和动力学参数等，来确定机器人的结构参数和传动方案，验算设计方案的合理性和可行性.等等。

凯恩法

凯恩法是由美国斯坦福大学应用力学教授Thomas R.Kane 在20世纪中叶提出的一种动力建模新方法，该方法与传统的分析力学思路存在很大的区别，因此被称之为虚功形式的达朗贝尔原理，其基本思想是以系统特点为依据，利将广义坐标的函数或者广义坐标替换为广义速度，并将其带入到相应的动力学方程当中，进一步可以求解出广义主动力等一系列变量。基于达朗贝尔原理可知，凯恩动力学方程的特点是既可以像拉格朗日法一样有效规避方程内的一系列内力项，使得求解过程大大简化。同时也能够获得如牛顿欧拉方法那样明确的物理含义。并且所求解的方程可以直接转化为不含特定因子的标准形式（Y=XU），这样能够大大提升方程的求解效率。

该方法是将达朗贝尔原理和虚位移原理推得的动力学普遍方程：$\sum \left(F_x-m_v{\ddot{r}}_v\right)\cdot \delta r_v=0$ ，进行了改进处理，推导出了系统的广义主动力和广义惯性力，广义主动力和广义惯性力相加等于零。

拉格朗日建模法

在牛顿力学中研究质点系的动力学经常使用直角坐标系，而对于拉格朗日方程法而言，该方法使用的动力学坐标系被称为广义坐标系。在该坐标系中可以构建支点系的动力学方程。18 世纪，拉格朗日在动力学普遍方程的基础上构建了更为简洁的动力学方程。这也是后人广为称赞的拉格朗日法，该方法概念简单，能够更为系统地表示出动力学的计算过程，其适用于完整系统，是经典力学发展中继牛顿定律后的又一个里程碑。
该方法原理简单，运算推导容易实现，尤其是针对较为复杂的机械系统，利用 该方法可以省去很多不必要的分析，从而较为容易的得到其数学模型，进而推导出其动力学方程。并且由 Lagrange 法推导的机器人动力学方程每一部分都有很具象的物理意义，对于由动力学分析其运动形态很有指导意义。

牛顿-欧拉方程法

牛顿-欧拉方程法本质是基于矢量力学的动力学建模方法，其通过将系统中所有单元都进行相应的隔离处理，并且基于牛顿第二定理等经典力学理论可以推导出质心的平动方程，以欧拉原理为基础可以获得系统内部不同单元的动力学方程，根据各个单元之间的约束关系，牛顿-欧拉方程可以建立单个刚体的动力学特性框架，对于多自由度多连杆机器人系统而言，其为一个多刚体系统。为建立系统整体动力学特性框架，需要迭代递推以建立每一个刚体的动力学特性框架，从而建立整个机器人系统的动力学特性框架。其动力学建模过程清晰。

利用牛顿-欧拉法建立机器人动力学方程，由正向运动学递推和逆向动力学递推两
个阶段构成。具体而言，正向运动学递推是指沿机器人基座到末端执行器对连杆的运动
状态进行计算；逆向动力学递推是指沿末端到基座计算各个连杆的力或力矩（惯性力、
惯性力矩等）。使用该方法建立动力学模型的优点在于可以迅速为机器人的实时控制确
定其所需的力或力矩。但是对于多自由度、多连杆等较为复杂的机器人系统而言，其建
模过程较为复杂，需要单独对机器人系统每个刚体建立方程，分析各个刚体之间的相互
作用力，效率较为低下。

空间算子代数法

以牛顿-欧拉方程为代表的矢量力学求解方法的计算效率通常能够达到系统自由度数目的3次方数量级；而已拉格朗日方程为代表的分析力学方法的计算效率通常为2次方数量级。这对于大型、复杂、多自由度的多体系统非常不利，并且机器人动力学实时仿真及其控制系统设计对于系统动力学计算过程提出了更为苛刻的要求。美国科学家Rodriguez 将卡尔曼滤波预测理论的状态方程与多体系统动力学进行比拟，发现了两者的内在联系，发展了O(n)阶多体系统动力学的空间算子代数法。其假设机器人由n个连杆（不含基座）组成，定义机器人连杆编号从末端到基座依次为0～n。在此基础上，定义由机器人末端向基座地推计算为包括力和力矩的递推的内向递推；定义从基座到机器人末端为包括速度和加速度的向外递推,在此基础上可以对机器人的运动关系进行有效分析，并定义机器人相邻杆件的速度、力、力矩递推算子，通过空间算子得到相邻连杆之间的变换关系，从而建立起多体系统动力学的空间算子代数体系。

建模方法对比

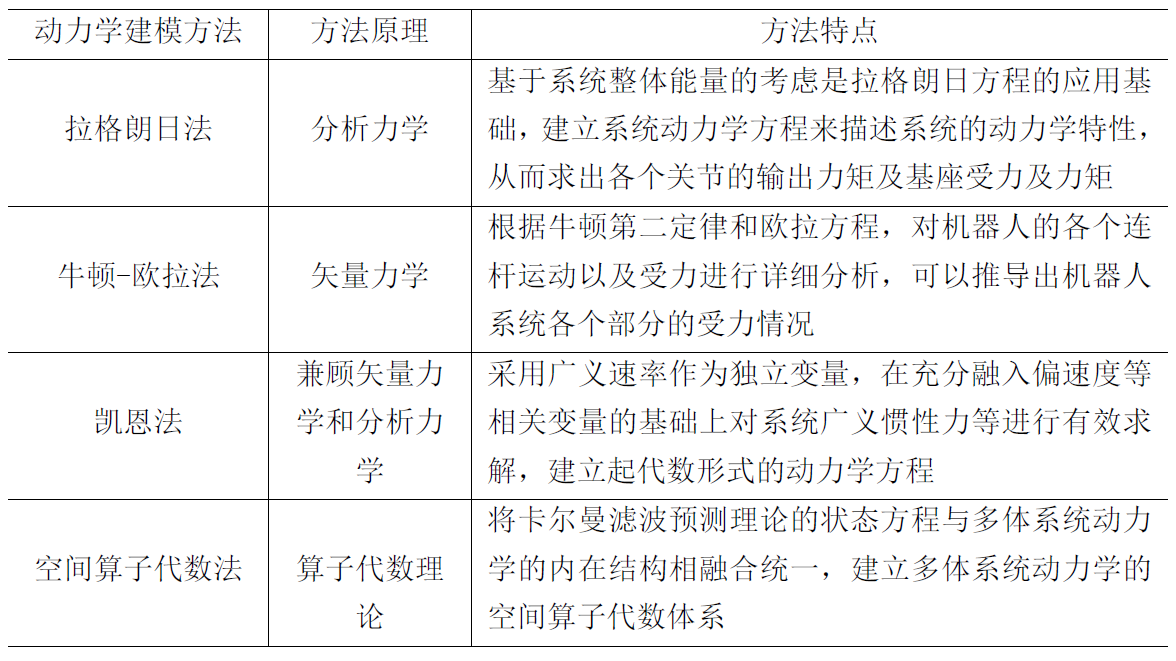
串联机器人拉格朗日建模法详解

当前对于机器人动力学的研究方法有很多种，其中比较常用的主要有拉格朗日法和牛顿-欧拉方法，考虑到拉格朗日法具有明确的物理意义，对于理解机器人的动力学模型更加有利，所以选择拉格朗日法对机器人的动力学相关问题进行研究与分析。详细步骤如下：

1. 整理系统的质量矩阵$m_i\in R_{1\times 6}$，各连杆的质心坐标系矩阵：
   

2. 计算各连杆惯性矩阵： $I_i$

3. 求解各连杆的伪惯性矩阵，公式如下：
   

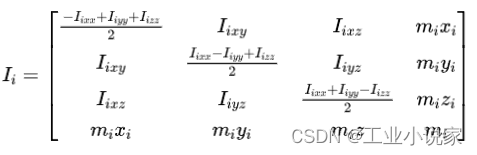
4. 机器人系统的总动能和势能为：

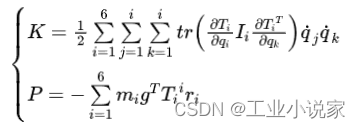
6. 带入拉格朗日函数L：

$$L=K-P$$

6. 由L可得动力学模型为：
   $${\tau }_i=\frac{d}{dt}\left(\frac{\partial L}{\partial {\dot{q}}_i}\right)-\frac{\partial L}{\partial q_i},i=\mathrm{1.2.3.4.5.6}$$

7. 整进一步整理可得：

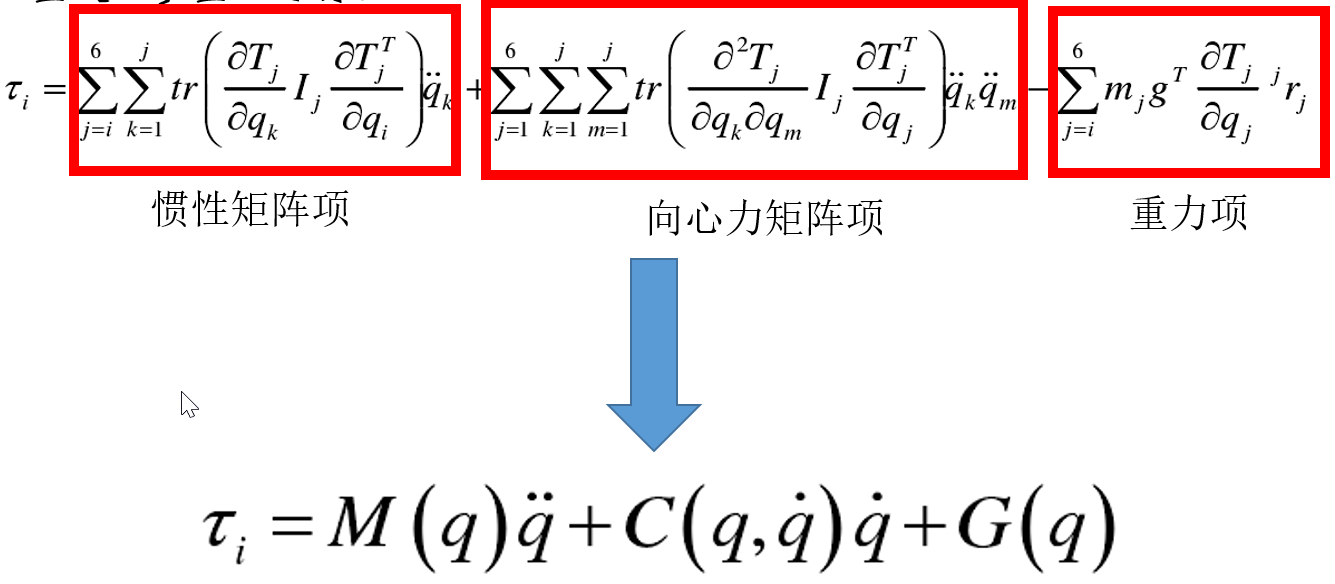
下篇推文将讲解如何基于MATLAB的机器人工具箱建立串联机器人的动力学模型。

往期推荐：