Spark算法之ALS模型（附Scala代码）

news2024/10/6 0:29:55

Spark算法之ALS模型（附Scala代码）

在大数据时代，个性化推荐系统已成为连接用户与信息的桥梁，而算法则是构建这一桥梁的基石。Apache Spark，作为一款强大的分布式计算系统，提供了丰富的机器学习库，其中ALS（交替最小二乘法）模型以其出色的性能和可扩展性，在处理大规模推荐系统问题中备受青睐。

ALS模型，作为矩阵分解技术的代表，能够有效捕捉用户与物品间的潜在关系，为用户提供精准的个性化推荐。

文章目录

Spark算法之ALS模型（附Scala代码）
一、什么是ALS模型
二、ALS模型原理
三、ALS模型求解流程
四、Spark实现代码
五、ALS模型参数解析

一、什么是ALS模型

ALS模型，全称为交替最小二乘法（Alternating Least Squares），是一种基于协同过滤思想的矩阵分解算法。它的核心思想是通过隐含特征（latent factors）联系用户兴趣和物品（item），基于用户的行为找出潜在的主题和分类，然后对物品进行自动聚类，划分到不同类别或主题（代表用户的兴趣）。

ALS算法的亮点之一在于优化参数时使用了交替最小二乘法，而非梯度下降算法，这使得ALS算法可以进行分布式并行计算。因此，它被广泛应用于大规模推荐系统中，如Apache Spark的Mllib库就包含了ALS算法的实现。

二、ALS模型原理

ALS（Alternating Least Squares，交替最小二乘法）模型是一个广泛用于推荐系统中的协同过滤技术，特别是在处理用户对物品的评分预测问题上。它的核心思想是通过矩阵分解技术来预测缺失的评分，从而为用户推荐可能感兴趣的物品。

在推荐系统中，通常会有一个用户-物品评分矩阵，其中包含了用户对物品的评分记录。在现实世界中，这个矩阵通常是非常稀疏的，因为每个用户只能对有限的物品进行评分。ALS的目标是填充这个矩阵中的缺失值，使得可以预测用户未评分的物品的评分。
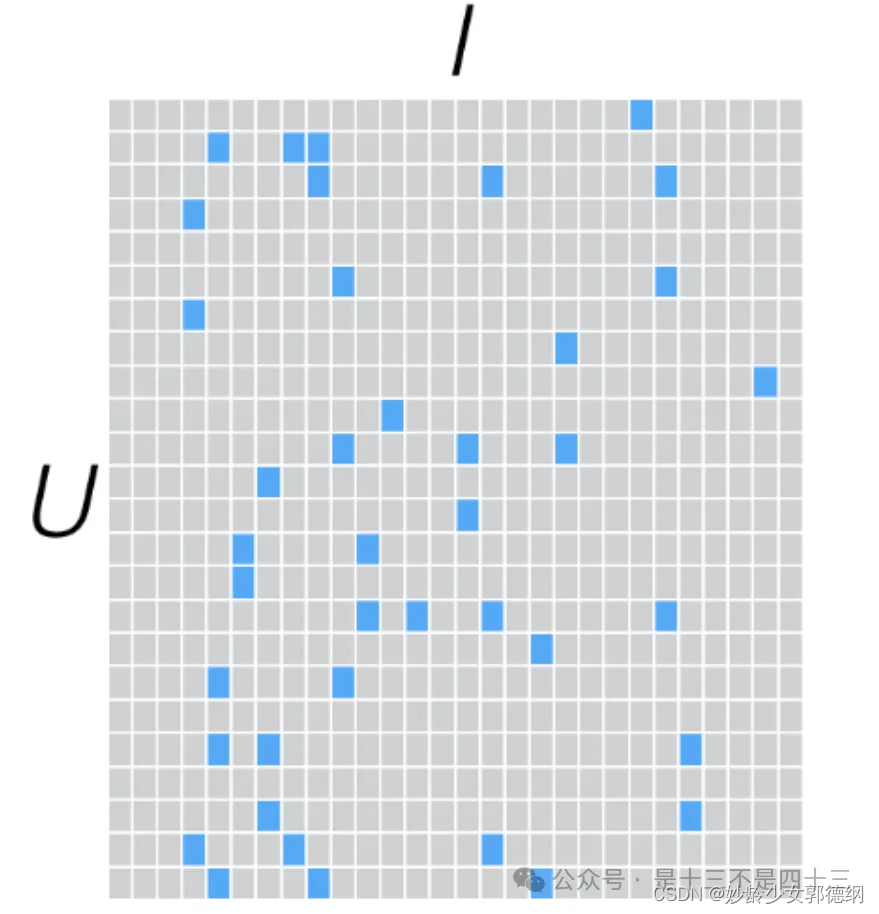
用户评分矩阵
针对这样的特点，可以假设用户和商品之间存在若干关联维度（比如用户年龄、性别、受教育程度和商品的外观、价格等），无需实际计算，只需要将R矩阵投射到这些维度上即可。这个投射的数学表示是：
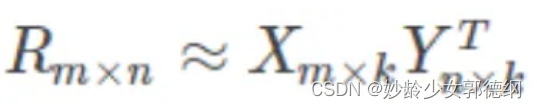
在这里插入图片描述
这个投射只是一个近似的空间变换。一般情况下，k的值远小于n和m的值，从而达到了数据降维的目的。

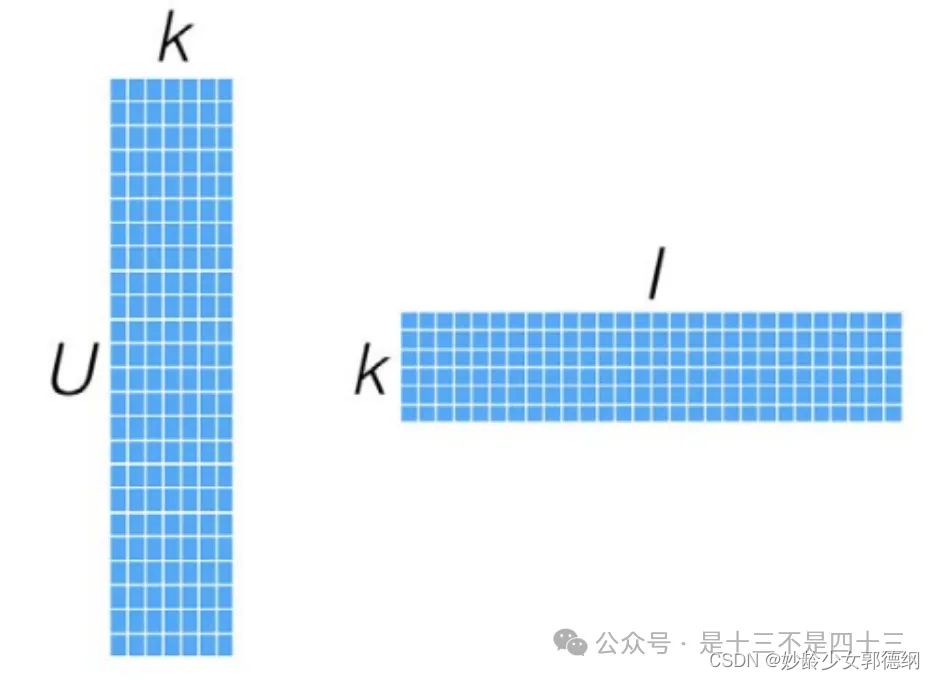
并不需要显式的定义这些关联维度，而只需要假定它们存在即可，因此这里的关联维度又被称为Latent factor。k的典型取值一般是20～200。