目录
- 1.两数之和
- 题目
- C++代码
- 2.两数相加
- 题目
- 代码
- 3. 无重复字符的最长子串
- 题目:
- 代码:
- 4. 合并两个有序数组
- 题目:
- 代码:
- 5.寻找两个正序数组的中位数
- 题目:
- 代码:
1.两数之和
题目
给定一个整数数组 nums 和一个整数目标值 target,请你在该数组中找出 和为目标值 target 的那 两个 整数,并返回它们的数组下标。
你可以假设每种输入只会对应一个答案。但是,数组中同一个元素在答案里不能重复出现。
你可以按任意顺序返回答案。
示例 1:
输入:nums = [2,7,11,15], target = 9
输出:[0,1]
解释:因为 nums[0] + nums[1] == 9 ,返回 [0, 1] 。
示例 2:
输入:nums = [3,2,4], target = 6
输出:[1,2]
示例 3:
输入:nums = [3,3], target = 6
输出:[0,1]
提示:
2 <= nums.length <= 104
-109 <= nums[i] <= 109
-109 <= target <= 109
只会存在一个有效答案
C++代码
vector容器 见C++相关博客
vector<int> twoSum(vector<int>& nums, int target) {
unordered_map<int, int> hashtable;
for (int i = 0; i < nums.size(); i++)
{
// 在哈希表中找 target-num[i]
// unordered_map<int,int>::iterator 可以用auto代替这一串冗长的代码
auto it = hashtable.find(target - nums[i]);
// 如果找到
if (it != hashtable.end()) {
// it->first指的是key,it->second指的是value
return { it->second, i };
}
// 如果找不到
hashtable[nums[i]] = i;
}
return {};
}
调试+调用
由于考研复试需要,无奈从Python转为C++,所有的代码操作都不熟悉,现将相关调试代码记录如下
int main() {
vector<int> nums;
vector<int> res;
for (int i = 0; i < 4; i++)
{
int a;
cin >> a;
nums.push_back(a);
}
int target;
cin >> target;
//函数调用
res = twoSum(nums, target);
//遍历容器
for (vector<int>::iterator it = res.begin(); it != res.end(); it++) {
cout << *it << " ";
}
cout << endl;
}
2.两数相加
题目
给你两个 非空 的链表,表示两个非负的整数。它们每位数字都是按照 逆序 的方式存储的,并且每个节点只能存储 一位 数字。
请你将两个数相加,并以相同形式返回一个表示和的链表。
你可以假设除了数字 0 之外,这两个数都不会以 0 开头。
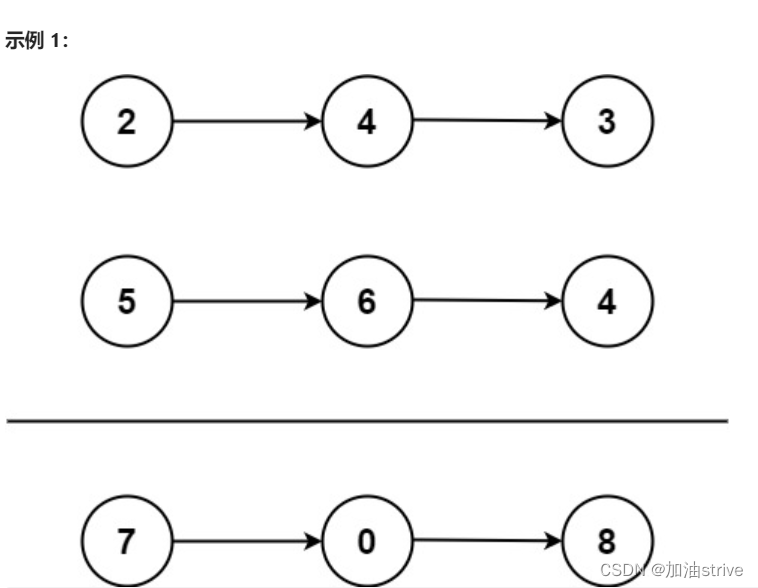
输入:l1 = [2,4,3], l2 = [5,6,4]
输出:[7,0,8]
解释:342 + 465 = 807.
示例 2:
输入:l1 = [0], l2 = [0]
输出:[0]
示例 3:
输入:l1 = [9,9,9,9,9,9,9], l2 = [9,9,9,9]
输出:[8,9,9,9,0,0,0,1]
代码
ListNode* addTwoNumbers(ListNode* l1, ListNode* l2) {
ListNode* head = nullptr, * tail = nullptr;
// 进位初始变量为0
int carry = 0;
while (l1 || l2) {
// 如果L1不为空,n1就为L1的第一个元素
// 也就是说 个位数先相加 L2类似
int n1 = l1 ? l1->val : 0;
int n2 = l2 ? l2->val : 0;
int sum = n1 + n2 + carry;
// 如果 head 为空指针
if (!head) {
head = tail = new ListNode(sum % 10);
}
// 如果 head 不是空指针
else {
tail->next = new ListNode(sum % 10);
tail = tail->next;
}
// 若sum>10 则进位为1
carry = sum / 10;
// L1 和 L2若存在其他位,向后移位
if (l1) {
l1 = l1->next;
}
if (l2) {
l2 = l2->next;
}
}
// 若最高位加完时,还有进位,那么新增一个最高位值为1 (即carry)
if (carry > 0) {
tail->next = new ListNode(carry);
}
return head;
}
3. 无重复字符的最长子串
题目:
示例 1:
输入: s = “abcabcbb”
输出: 3
解释: 因为无重复字符的最长子串是 “abc”,所以其长度为 3。
示例 2:
输入: s = “bbbbb”
输出: 1
解释: 因为无重复字符的最长子串是 “b”,所以其长度为 1。
示例 3:
输入: s = “pwwkew”
输出: 3
解释: 因为无重复字符的最长子串是 “wke”,所以其长度为 3。
请注意,你的答案必须是 子串 的长度,“pwke” 是一个子序列,不是子串。
代码:
s.substr(i, rk - i + 1)
第一个参数是从i开始截取,第二个参数是截取几个元素
int lengthOfLongestSubstring(string s) {
// 哈希集合,记录每个字符是否出现过
unordered_set<char> occ;
int n = s.size();
// 右指针,初始值为 -1,相当于我们在字符串的左边界的左侧,还没有开始移动
int rk = -1, ans = 0;
// 枚举左指针的位置,初始值隐性地表示为 -1
for (int i = 0; i < n; ++i) {
if (i != 0) {
// 左指针向右移动一格,移除一个字符
occ.erase(s[i - 1]);
}
// occ.count 存在该元素返回1,不存在该元素返回0
while (rk + 1 < n && !occ.count(s[rk + 1])) {
// 不断地移动右指针
occ.insert(s[rk + 1]);
rk++;
}
// 第 i 到 rk 个字符是一个极长的无重复字符子串
cout << s.substr(i, rk - i + 1)<<'\n';
ans = max(ans, rk - i + 1);
}
return ans;
}
int main() {
string str = "abcabcbb";
cout << lengthOfLongestSubstring(str);
}
4. 合并两个有序数组
本题是第五题的铺垫
代码参考王道考研教材
题目:
给你两个按 非递减顺序 排列的整数数组 nums1 和 nums2,另有两个整数 m 和 n ,分别表示 nums1 和 nums2 中的元素数目。
请你 合并 nums2 到 nums1 中,使合并后的数组同样按 非递减顺序 排列。
注意:最终,合并后数组不应由函数返回,而是存储在数组 nums1 中。为了应对这种情况,nums1 的初始长度为 m + n,其中前 m 个元素表示应合并的元素,后 n 个元素为 0 ,应忽略。nums2 的长度为 n 。
示例 1:
输入:nums1 = [1,2,3,0,0,0], m = 3, nums2 = [2,5,6], n = 3
输出:[1,2,2,3,5,6]
解释:需要合并 [1,2,3] 和 [2,5,6] 。
合并结果是 [1,2,2,3,5,6] ,其中斜体加粗标注的为 nums1 中的元素。
示例 2:
输入:nums1 = [1], m = 1, nums2 = [], n = 0
输出:[1]
解释:需要合并 [1] 和 [] 。
合并结果是 [1] 。
示例 3:
输入:nums1 = [0], m = 0, nums2 = [1], n = 1
输出:[1]
解释:需要合并的数组是 [] 和 [1] 。
合并结果是 [1] 。
注意,因为 m = 0 ,所以 nums1 中没有元素。nums1 中仅存的 0 仅仅是为了确保合并结果可以顺利存放到 nums1 中。
代码:
void merge(vector<int>& nums1, int m, vector<int>& nums2, int n) {
// K是sorted 数组的指针
int p1 = 0, p2 = 0,k = 0;
int *sorted = new int[m+n];
// 若p1和p2都没有到数组末尾
while (p1 < m && p2 < n) {
if (nums1[p1] <= nums2[p2]) {
sorted[k++] = nums1[p1++];
}
else {
sorted[k++] = nums2[p2++];
}
}
// 若P1还没有结束
while (p1 < m) {
sorted[k++] = nums1[p1++];
}
// 若P2还没有结束
while (p2 < n) {
sorted[k++] = nums2[p2++];
}
// 复制整个数组给nums1,并返回
for (int i = 0; i != m + n; ++i) {
nums1[i] = sorted[i];
}
}
测试:
int main() {
vector<int> a = { 1,2,3,0,0,0 };
int m = 3;
vector<int> b = { 2,5,6 };
int n = 3;
merge(a, m, b, n);
for (int i = 0; i < a.size(); i++) {
cout << a[i] <<" ";
}
}
5.寻找两个正序数组的中位数
本题(log (m+n))时间复杂度的代码思路太难想了,出于应试考虑,修改了上题的一部分代码,时间复杂度达到了(m+n)/2
题目:
给定两个大小分别为 m 和 n 的正序(从小到大)数组 nums1 和 nums2。请你找出并返回这两个正序数组的 中位数 。
算法的时间复杂度应该为 O(log (m+n)) 。
示例 1:
输入:nums1 = [1,3], nums2 = [2]
输出:2.00000
解释:合并数组 = [1,2,3] ,中位数 2
示例 2:
输入:nums1 = [1,2], nums2 = [3,4]
输出:2.50000
解释:合并数组 = [1,2,3,4] ,中位数 (2 + 3) / 2 = 2.5
代码:
double findMedianSortedArrays(vector<int>& nums1, vector<int>& nums2) {
int p1 = 0, p2 = 0,k = 0,num;
int m = nums1.size();
int n = nums2.size();
int* sorted = new int[m + n];
num = (m + n) / 2;
// 如果是偶数
if ((m + n) % 2 == 0) {
while (p1 < m && p2 < n && k <= num) {
if (nums1[p1] <= nums2[p2]) {
sorted[k++] = nums1[p1++];
}
else {
sorted[k++] = nums2[p2++];
}
}
while (p1 < m && k <= num) {
sorted[k++] = nums1[p1++];
}
while (p2 < n && k <= num) {
sorted[k++] = nums2[p2++];
}
double medium = double(sorted[k - 1] + sorted[k - 2]) / 2;
return medium;
}
// 如果是奇数
else
{
while (p1 < m && p2 < n && k <= num) {
if (nums1[p1] <= nums2[p2]) {
sorted[k++] = nums1[p1++];
}
else {
sorted[k++] = nums2[p2++];
}
}
while (p1 < m && k <= num) {
sorted[k++] = nums1[p1++];
}
while (p2 < n && k <= num) {
sorted[k++] = nums2[p2++];
}
double medium = double(sorted[k - 1]);
return medium;
}
}
测试:
int main() {
vector<int> a = { 1,3,5 };
vector<int> b = { 2,4,6,7 };
double res;
res = findMedianSortedArrays(a, b);
cout << res << "\n";
}

![[Lua实战]整理Lua中忽略的问题](https://img-blog.csdnimg.cn/720df27435104c098057007dd895507e.png)






![[Lua实战]Skynet-1.如何启动(linux环境启动)[开箱可用]](https://img-blog.csdnimg.cn/9ba41846f0a84d89ac5449bed97b462c.png)