多项式回归（Linear Regression）原理详解及Python代码示例

news2024/11/18 6:02:03

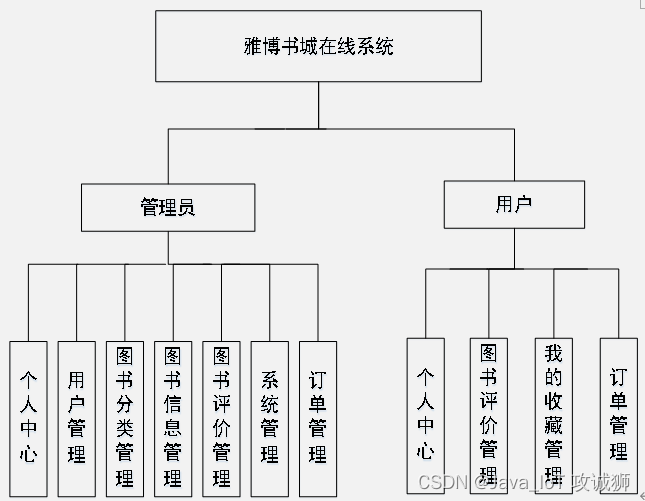
多项式回归原理详解

多项式回归（Polynomial Regression）是线性回归（Linear Regression）的一种扩展形式。它通过在输入变量上添加高次项来拟合非线性关系。虽然多项式回归本质上还是线性模型，但它允许模型在输入特征的多项式基础上进行线性拟合，从而捕捉复杂的非线性关系。

1. 多项式回归的数学表达式

假设我们有一个输入特征 x 和输出变量 y，多项式回归模型可以表示为：

y=β0+β1x+β2x2+β3x3+⋯+βnxn+ϵ

其中，β0,β1,β2,…,βn是模型的参数，n 是多项式的阶数，ϵ是误差项。

2. 多项式回归的步骤

选择多项式的阶数：选择合适的多项式阶数 n 是模型拟合的关键。阶数过低可能会导致欠拟合，阶数过高则可能导致过拟合。
构建多项式特征：将输入特征扩展为多项式特征。例如，对于一个一维特征 x，构建的特征矩阵为
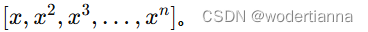
拟合模型：使用线性回归方法在多项式特征上进行拟合。
评估模型：通过均方误差（MSE）等指标评估模型的性能。

Python代码示例

以下是一个完整的Python代码示例，用于实现多项式回归。我们将使用scikit-learn库来构建和评估模型。

import numpy as np
import matplotlib.pyplot as plt
from sklearn.preprocessing import PolynomialFeatures
from sklearn.linear_model import LinearRegression
from sklearn.metrics import mean_squared_error

# 生成一些示例数据
np.random.seed(0)
x = 2 - 3 * np.random.normal(0, 1, 100)
y = x - 2 * (x ** 2) + np.random.normal(-3, 3, 100)

# 将数据转化为二维数组
x = x[:, np.newaxis]
y = y[:, np.newaxis]

# 可视化原始数据
plt.scatter(x, y, s=10)
plt.title("Original Data")
plt.show()

# 创建多项式特征（例如，二次多项式）
poly = PolynomialFeatures(degree=2)
x_poly = poly.fit_transform(x)

# 创建线性回归模型并在多项式特征上进行拟合
model = LinearRegression()
model.fit(x_poly, y)

# 预测结果
y_pred = model.predict(x_poly)

# 可视化拟合结果
plt.scatter(x, y, s=10, label='Original data')
plt.plot(x, y_pred, color='r', label='Fitted polynomial')
plt.title("Polynomial Regression (degree=2)")
plt.legend()
plt.show()

# 打印模型参数和均方误差
print("Coefficients:", model.coef_)
print("Intercept:", model.intercept_)
print("Mean Squared Error:", mean_squared_error(y, y_pred))

# 尝试不同的多项式阶数
degrees = [1, 2, 3, 4, 5]
for degree in degrees:
    poly = PolynomialFeatures(degree=degree)
    x_poly = poly.fit_transform(x)
    model = LinearRegression()
    model.fit(x_poly, y)
    y_pred = model.predict(x_poly)
    
    plt.scatter(x, y, s=10, label='Original data')
    plt.plot(x, y_pred, label=f'Degree {degree}')
    plt.title(f"Polynomial Regression (degree={degree})")
    plt.legend()
    plt.show()
    
    print(f"Degree {degree} - Coefficients:", model.coef_)
    print(f"Degree {degree} - Intercept:", model.intercept_)
    print(f"Degree {degree} - Mean Squared Error:", mean_squared_error(y, y_pred))