每日一题——力扣100. 相同的树（举一反三+思想解读+逐步优化）四千字好文

一个认为一切根源都是“自己不够强”的INTJ

个人主页：用哲学编程-CSDN博客
专栏：每日一题——举一反三
Python编程学习
Python内置函数

Python-3.12.0文档解读

我的写法

代码分析

时间复杂度分析

空间复杂度分析

总结

我要更强

时间复杂度和空间复杂度分析

哲学和编程思想

递归与迭代的哲学：

分而治之（Divide and Conquer）：

抽象与具体化：

空间与时间的权衡：

数据结构的选择：

算法优化：

举一反三

题目链接：https://leetcode.cn/problems/same-tree/description/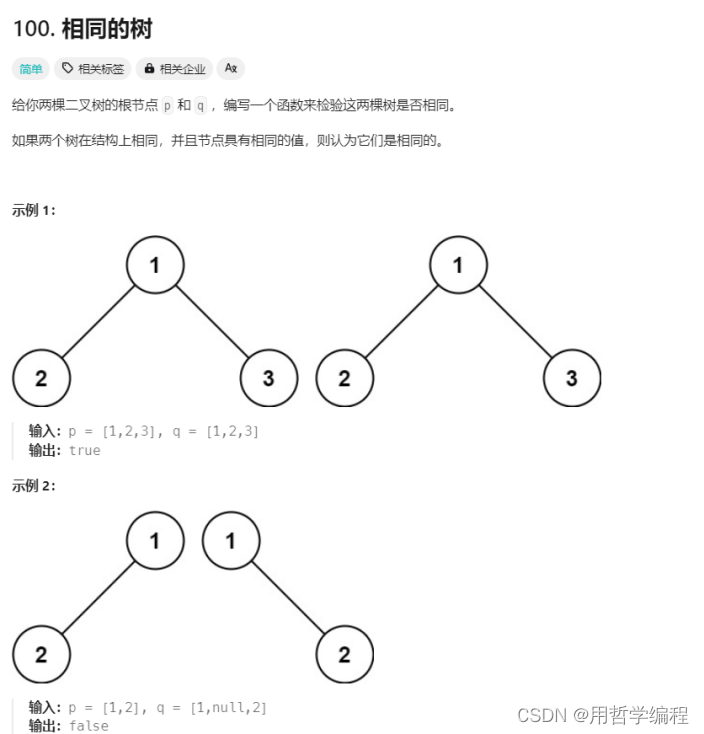

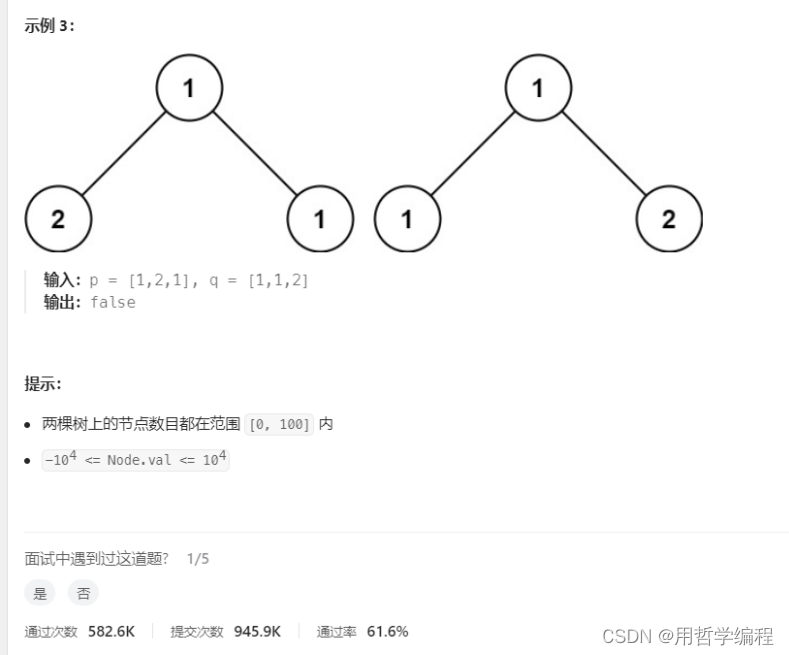
我的写法

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     struct TreeNode *left;
 *     struct TreeNode *right;
 * };
 */
/*
解题思路：
首先比较根节点是否相同，然后分别比较左右子树是否相同。
*/
bool isSameTree(struct TreeNode* p, struct TreeNode* q){
    if(p == NULL && q != NULL)
        return false;
    if(p != NULL && q == NULL)
        return false;
    if(p == NULL && q == NULL)
        return true;
    
    if(p->val == q->val)
        return  isSameTree(p->left, q->left)
                && isSameTree(p->right, q->right);
    else
        return false;
}

这段代码是用于判断两棵二叉树是否相同的算法。下面是对这段代码的专业点评：

代码分析

边界条件处理：
- 代码首先处理了两个节点都为空的情况，此时认为两棵树相同。
- 然后处理了其中一个节点为空而另一个不为空的情况，此时认为两棵树不同。
递归比较：
- 当两个节点都不为空时，比较它们的值是否相等。
- 如果值相等，则递归地比较它们的左子树和右子树。
返回值：

如果两个节点的值不相等，直接返回false。
如果值相等，返回左子树和右子树比较结果的逻辑与（&&）。

时间复杂度分析

最坏情况：每棵树的每个节点都需要被访问一次，因此时间复杂度为O(n)，其中n是节点数较多的那棵树的节点总数。
平均情况：同样为O(n)。

空间复杂度分析

最坏情况：如果树是完全不平衡的（例如，每个节点都只有一个子节点），递归调用的栈深度将达到n，因此空间复杂度为O(n)。
平均情况：如果树是平衡的，递归调用的栈深度将大约为log(n)，因此空间复杂度为O(log n)。

总结

这段代码简洁高效，正确地实现了判断两棵二叉树是否相同的功能。通过递归的方式，代码逻辑清晰，易于理解和维护。时间复杂度在最坏情况下为O(n)，空间复杂度在最坏情况下为O(n)，在平均情况下为O(log n)，这使得它在处理大规模数据时也能保持较好的性能。

我要更强

为了优化时间复杂度和空间复杂度，我们可以考虑以下几种方法：

迭代方法（使用栈）：这种方法通过使用栈来模拟递归过程，可以减少递归调用栈的空间消耗。
前序遍历：通过前序遍历两棵树，并比较每个节点的值，可以确保两棵树的结构和值都相同。

下面是使用迭代方法（使用栈）的完整代码：

#include <stdbool.h>
#include <stdlib.h>

// 定义树节点结构
struct TreeNode {
    int val;
    struct TreeNode *left;
    struct TreeNode *right;
};

bool isSameTree(struct TreeNode* p, struct TreeNode* q) {
    // 使用栈来模拟递归过程
    struct TreeNode** stackP = (struct TreeNode**)malloc(sizeof(struct TreeNode*));
    struct TreeNode** stackQ = (struct TreeNode**)malloc(sizeof(struct TreeNode*));
    int topP = -1;
    int topQ = -1;

    // 将根节点入栈
    if (p != NULL) {
        stackP[++topP] = p;
    }
    if (q != NULL) {
        stackQ[++topQ] = q;
    }

    while (topP >= 0 || topQ >= 0) {
        // 出栈并比较节点
        if (topP < 0 || topQ < 0) {
            // 如果其中一个栈已经空了，说明两棵树不同
            return false;
        }

        struct TreeNode* nodeP = stackP[topP--];
        struct TreeNode* nodeQ = stackQ[topQ--];

        if (nodeP->val != nodeQ->val) {
            // 如果节点值不同，返回false
            return false;
        }

        // 将左右子节点入栈
        if (nodeP->right != NULL) {
            stackP[++topP] = nodeP->right;
        }
        if (nodeQ->right != NULL) {
            stackQ[++topQ] = nodeQ->right;
        }
        if (topP < 0 || topQ < 0) {
            // 如果其中一个栈已经空了，说明两棵树不同
            return false;
        }

        if (nodeP->left != NULL) {
            stackP[++topP] = nodeP->left;
        }
        if (nodeQ->left != NULL) {
            stackQ[++topQ] = nodeQ->left;
        }
        if (topP < 0 || topQ < 0) {
            // 如果其中一个栈已经空了，说明两棵树不同
            return false;
        }
    }

    // 释放动态分配的内存
    free(stackP);
    free(stackQ);

    // 如果所有节点都相同，返回true
    return true;
}

时间复杂度和空间复杂度分析

时间复杂度：O(n)，其中n是节点数较多的那棵树的节点总数。每个节点都会被访问一次。
空间复杂度：O(n)，在最坏情况下，栈的大小可以达到树的深度，即树的节点数。

这种方法通过使用栈来模拟递归，减少了递归调用栈的空间消耗，但并没有减少时间复杂度。在实际应用中，这种方法的性能可能会受到栈操作的影响，但对于大多数情况，它仍然是一个有效的解决方案。

哲学和编程思想

在解决这个问题时，我们运用了以下哲学和编程思想：

递归与迭代的哲学：
- 递归：递归是一种自我调用的方法，它依赖于问题的分解，将大问题分解为小问题，直到问题变得足够简单可以直接解决。在原始的递归解决方案中，我们使用了递归的思想来比较两棵树的节点。
- 迭代：迭代是通过循环结构重复执行一组操作，直到满足某个条件为止。在优化后的解决方案中，我们使用栈来模拟递归过程，这是一种迭代的思想。迭代通常比递归更节省空间，因为它避免了函数调用栈的额外开销。
分而治之（Divide and Conquer）：
- 这个策略是将一个复杂的问题分解成两个或更多的相同或相似的子问题，再将子问题分解，直到最后子问题可以简单的直接求解，原问题的解即子问题的解的合并。在比较两棵树是否相同的问题中，我们通过递归地比较左右子树来实现分而治之的思想。
抽象与具体化：
- 在编程中，我们抽象出树的节点结构，并定义了节点之间的关系（左右子节点）。这种抽象使得我们可以专注于树的逻辑结构，而不必关心具体的实现细节。
空间与时间的权衡：
- 在优化解决方案时，我们考虑了空间和时间的权衡。原始的递归解决方案在时间上是高效的（O(n)），但在空间上可能会有较高的开销（O(n)的递归调用栈）。通过使用迭代和栈，我们减少了空间的使用，但时间复杂度保持不变。
数据结构的选择：
- 栈是一种后进先出（LIFO）的数据结构，它在处理树的遍历问题时非常有用。在这个问题中，我们使用栈来存储待比较的节点，这是一种有效的数据结构选择，因为它模拟了递归调用的过程。
算法优化：

通过将递归转换为迭代，我们优化了算法的空间复杂度。这是一种常见的算法优化技巧，特别是在处理深度较大的树时，可以避免栈溢出的风险。

这些哲学和编程思想是解决复杂问题时常用的方法，它们帮助设计出更高效、更易于理解和维护的代码。在实际编程中，理解这些思想并灵活运用它们是非常重要的。

举一反三

掌握这些哲学和编程思想后，你可以将它们应用到更广泛的编程和问题解决场景中。以下是一些技巧，帮助举一反三：

递归与迭代的转换：
- 当你遇到一个递归问题时，思考是否可以通过迭代和适当的数据结构（如栈或队列）来解决。这种转换通常可以减少空间复杂度，避免递归带来的额外开销。
分而治之策略：
- 对于复杂问题，尝试将其分解为更小的、可管理的部分。例如，在处理数组或字符串问题时，可以考虑将它们分割成子数组或子串，分别处理后再合并结果。
抽象与具体化：
- 在设计数据结构或算法时，首先抽象出问题的核心概念和关系，然后具体化这些概念以实现代码。例如，在设计一个社交网络应用时，首先抽象出用户、关系和消息等概念，然后定义这些概念的具体实现。
空间与时间的权衡：
- 在优化算法时，始终考虑时间和空间的权衡。有时为了提高时间效率，可能需要牺牲一些空间；反之亦然。理解这种权衡可以帮助你做出更合理的决策。
选择合适的数据结构：
- 根据问题的特点选择合适的数据结构。例如，如果问题涉及元素的插入和删除，链表可能是一个好选择；如果需要快速查找，数组或哈希表可能更合适。
算法优化：
- 不断寻找改进算法的机会。例如，使用动态规划来避免重复计算，或者使用位操作来提高效率。
模式识别：
- 学会识别问题中的常见模式，如树的遍历、图的搜索、排序和搜索算法等。一旦识别出模式，就可以应用已知的解决方案或算法。
测试和调试：
- 在编写代码时，始终考虑如何测试和调试。良好的测试策略可以帮助你快速发现和修复问题。
代码重用：
- 尽可能重用代码。如果某个功能或算法已经在其他地方实现，考虑是否可以直接使用或稍作修改后使用。
持续学习：