玫瑰少年：点击收听

1 基本知识点

1、根结点：在一棵树中，(唯一)一个没有前驱的结点
2、叶子结点：在一棵树中，没有后继的结点
3、结点的度：是指结点后继的数量
4、树的度：是指所有结点度的最大值
5、祖先结点：找到某一结点，逐渐向上，直到走到根结点，所走过的结点都是该结点的祖先结点
6、结点所在的层次：根结点位于第一层
7、树的高度：树中结点最高处于的层次数
8、森林：多棵树可以构成森林
9、满二叉树：如果一棵二叉树中任意一层的结点个数都已经达到最大值，那么这棵二叉树就是满二叉树
10、给满二叉树编号的方式：从上到下、从左到右

注意：当你删除一些结点之后,编号不会发生改变

11、完全二叉树：编号连续

注意：对于深度为k的完全二叉树,其前k-1层一定是满的,第k层可以是满的,也可以是不满的,**满二叉树也属于完全二叉树**

12、满二叉树一定是完全二叉树，但是完全二叉树不一定是满二叉树
13、一棵二叉树的度可以小于2(单支树)
14、完全二叉树中,若一个结点没有左孩子,那么它一定是树叶
15、在含有n个结点的树中,边数只可以为n-1条

---

2 基本结论

1、一棵高度为k的满二叉树具有2^k-1个结点
2、满二叉树的编号方式的实现：

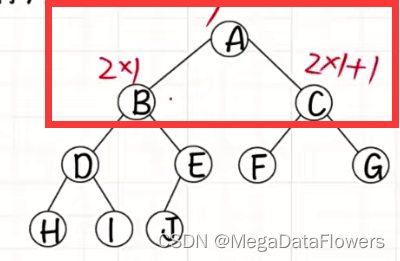
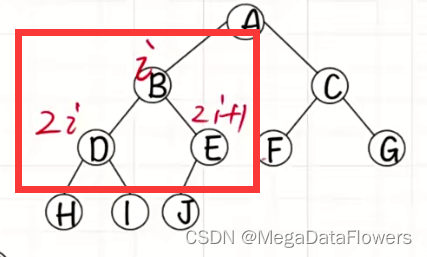
解释：某一结点为i,其左孩子的编号为2*i,右孩子的编号为2*i+1

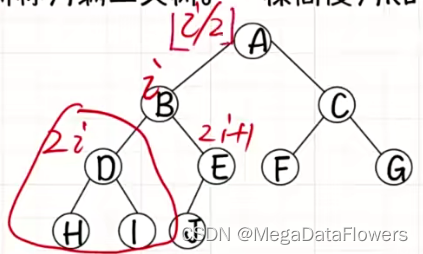
解释：如果知道该结点的编号为i,那么其双亲结点编号为floor(i/2)  floor()代表向下取整(小于等于)

---

3 二叉树的性质

1、

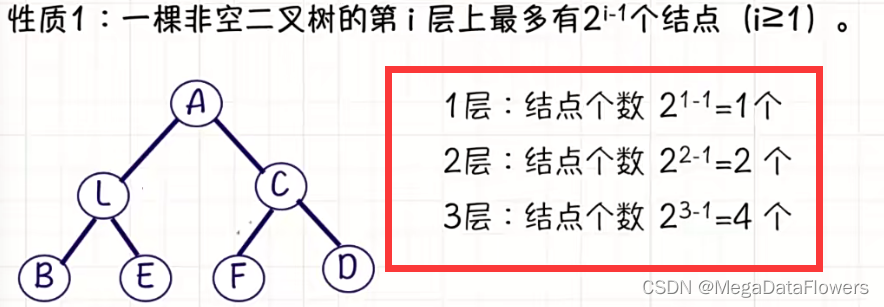
2、

3、

解释：
1 二叉树的结点总数n = n0+n1+n2(结点为0+结点为1+结点为2)之和
2 假设B为分支总数,一棵二叉树如果有3个结点,就有2个分支(除了根结点以外,其他结点都有前驱)
3 所以说B = n-1(n为结点总数)
4 同时：B = n1*1+n2*2(n1表示分支为1,n2表示分支为2,最后求和)
5 因为n = n0+n1+n2
6 所以说n-1 = n0+n1+n2-1 = B
7 那么,n1+2n2 = n0+n1+n2-1
8 n0 = n2 + 1

4、

解释：
1 向上取整ceil(x) 大于等于x的最小整数
2 向下取整floor(x) 小于等于x的最大整数

5、

---

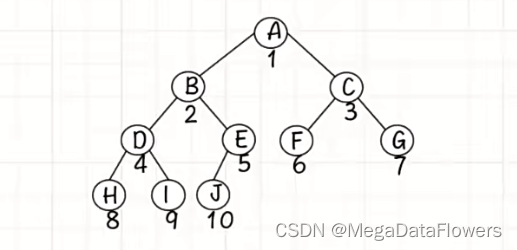
4 题目练习

1、
注意：完全二叉树存在一种特殊情况：最后两层都没有填完(就是倒数第二层存在叶子结点,最后一层也存在叶子结点)

解析：
1 获取完全二叉树的最多结点数目就需要考虑这种情况
2 因为第6层有8个叶子结点,那么该完全二叉树最多有7层(第6、7层都存在叶子结点)
3 因为第6层的结点数目最多为：2的6减1次方个结点 = 32个
4 32-8=24个(24个结点是非叶子结点)
5 假设这第6层的24个非叶子结点都有2个分支：24*2 = 48个
6 那么第7层就有48个叶子结点,加上前6层的结点数目：2的6次方-1 = 63个结点
7 该完全二叉树最多有63+48个结点=111个

2、如果将上一道题目改为求：该完全二叉树的最少结点数目？

解析：
1 将第6层作为最后一层
2 倒数第二层：第5层
3 前5层一共有2的5次方减1个结点 = 31个
4 加上第六层的8个
5 最少为39个结点

3、

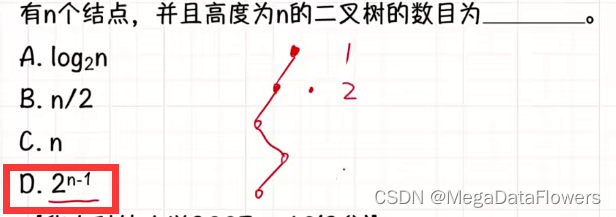
解析：
1 有n个结点,并且高度为n的二叉树称为单支树
2 除了根结点不区分是左右子树
3 剩下的n-1个结点都可以区分左右两种情况
4 所以说数目为：2的(n-1)次方个

4、

5、
注意：在完全二叉树中,度为1的结点数目是小于等于1的



6、

如果题目要求最多的情况：前k层为满二叉树(2^k-1个)
7、
8、

最少有247个结点(n1 = 0)

9、

总结：
1 度为3的数：n0 = 1*n2+2*n3+1

2 度为4的数：n0 = 1*n2+2*n3+3*n4+1

3 度为k的数：n0 = 1*n2+2*n3+3*n4+...+(k-1)*nk+1

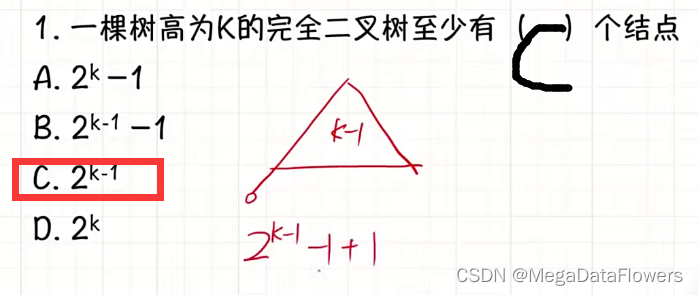
10、

解析：
1 该二叉树的类型不确定
2 如果是单支树那么为n
3 如果是完全二叉树那么选C