1.KNN
1.新增数据的分类
import pandas as pd
# 您的原始数据字典
data = {
'电影名称': ['电影1', '电影2', '电影3', '电影4', '电影5'],
'打斗镜头': [10, 5, 108, 115, 20],
'接吻镜头': [110, 89, 5, 8, 200],
'电影类型': ['爱情片', '爱情片', '动作片', '动作片', '爱情片']
}
# 将数据字典转换为DataFrame
df = pd.DataFrame(data)
# 定义一个简单的分类逻辑(这里只是一个示例,您可以根据数据调整阈值)
def predict_movie_type(fights, kisses):
if fights > kisses:
return '动作片'
else:
return '爱情片'
# 输入您想要预测的电影数据
input_fights = float(input("请输入打斗镜头的数量: "))
input_kisses = float(input("请输入接吻镜头的数量: "))
# 预测电影类型
predicted_type = predict_movie_type(input_fights, input_kisses)
print(f"基于您输入的数据,电影类型被预测为: {predicted_type}")
2.把新增数据放在散点图上并标记坐标
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
# 您的修正后的数据字典
data = {
'电影名称': ['电影1', '电影2', '电影3', '电影4', '电影5'],
'打斗镜头': [10, 5, 108, 115, 120],
'接吻镜头': [110, 89, 5, 8, 20],
'电影类型': ['爱情片', '爱情片', '动作片', '动作片', '动作片']
}
pd_data = pd.DataFrame(data)
colors = ['red' if t == '爱情片' else 'green' for t in pd_data['电影类型']]
# 设置中文字体,以便正确显示中文标签和标题
plt.rcParams['font.sans-serif'] = ['SimHei'] # 使用黑体字体显示中文
plt.rcParams['axes.unicode_minus'] = False # 正确显示负号
# 创建图形和散点图
plt.figure()
# 绘制散点图并添加坐标
for index, row in pd_data.iterrows():
plt.scatter(row['打斗镜头'], row['接吻镜头'], c=colors[index])
plt.annotate(f'({row["打斗镜头"]}, {row["接吻镜头"]})',
(row['打斗镜头'], row['接吻镜头']),
textcoords="offset points", xytext=(0,10), ha='center')
plt.grid(linestyle='-.')
plt.xlim(0, 140)
plt.ylim(0, 220) # 调整y轴范围以适应新的数据
plt.xlabel("打斗镜头")
plt.ylabel("接吻镜头")
plt.title("电影分析")
# 添加图例
legend_elements = [plt.Line2D([0], [0], color='red', label='爱情片'),
plt.Line2D([0], [0], color='green', label='动作片')]
plt.legend(handles=legend_elements, loc='best')
# 显示图形
plt.show()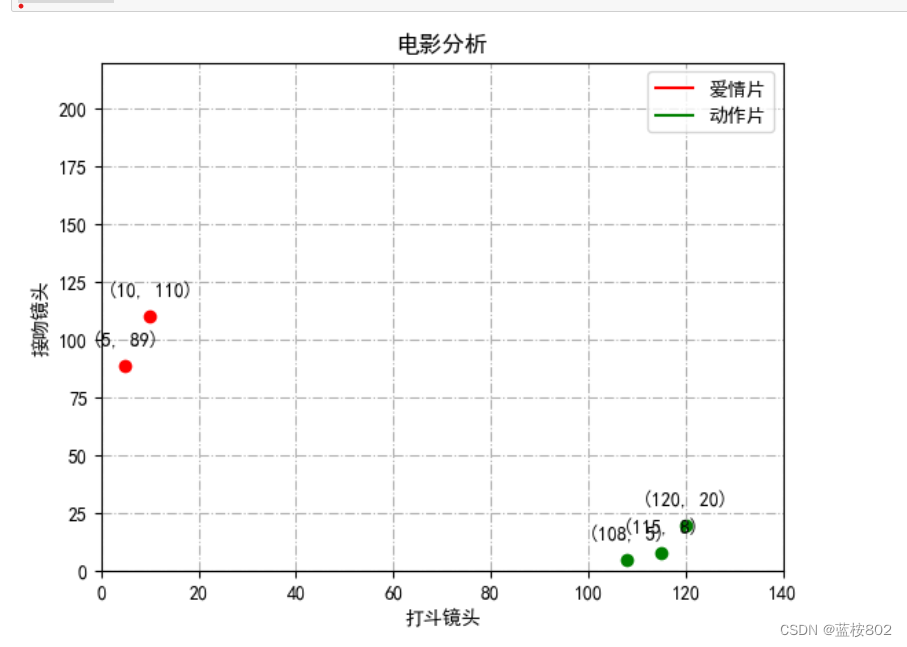
2.logistic回归,用线性来划分两个类型
import matplotlib.pyplot as plt
import numpy as np
#用回归思想作二分类(线性回归 wx+b),用激活函数(sigmoid函数)来转为0 1的结果进行分类【z=wx+b】。
#x:为样本的输入特征向量,w和b:w为模型权重参数参数,b为偏置。当确定w和b时,可确定模型
#所以,需要损失函数来确定最优的w和b(随机事件越不确定,所包含的信息量就越多,熵越大)
#则,样本所属类别的概率,而这个概率越大越好,所以也就是求解这个损失函数的最大值。
#怎么求解使J(θ)最大的θ值呢?因为是求最大值,所以我们需要使用梯度上升算法。
#(个人理解θ就是w0,w1,w2)"""
def loadDataSet():
dataMat = [] #创建数据列表
labelMat = [] #创建标签列表
fr = open('testSet.txt') #打开文件
for line in fr.readlines(): #逐行读取
lineArr = line.strip().split() #去回车,放入列表,以空格分割split,并去掉空格strip
dataMat.append([1.0, float(lineArr[0]), float(lineArr[1])]) #添加数据,
#lineArr[0]放w,lineArr[1]放x
#z=w0x0 + w1x1 + w2x2,即可将数据分割开。其中,x0为全是1的向量,x1为数据集的第一列数据,x2为数据集的第二列数据。
#另z=0,则0=w0 + w1x1 + w2x2。横坐标为x1,纵坐标为x2。这个方程未知的参数为w0,w1,w2,也就是我们需要求的回归系数(最优参数)。
labelMat.append(int(lineArr[2])) #添加标签,第三列标签
#labelMat即为分类标签。根据标签的不同,对这些点进行分类。
fr.close() #关闭文件
return dataMat, labelMat #返回
if __name__=='__main__':
dataMat,labelMat=loadDataSet()
print(dataMat)
print(labelMat)

def plotDataSet():
dataMat, labelMat = loadDataSet() #加载数据集
dataArr = np.array(dataMat) #转换成numpy的array数组
n = np.shape(dataMat)[0] #数据个数(读取一维dataMat矩阵的长度)
xcord1 = []; ycord1 = [] #正样本
xcord2 = []; ycord2 = [] #负样本
for i in range(n): #根据数据集标签进行分类
if int(labelMat[i]) == 1:
xcord1.append(dataArr[i,1]); ycord1.append(dataArr[i,2]) #1为正样本
#dataArr[i,1]:表示dataArr[]数组中下标为1的第i个元素
else:
xcord2.append(dataArr[i,1]); ycord2.append(dataArr[i,2]) #0为负样本
fig = plt.figure()#创建一个绘图对象
ax = fig.add_subplot(111) #添加subplot
#add_subplot(111),a=1,b=1,c=1,表示把他的行和列都分为1份,
#其实就是保持不变,所以子图只有1*1=1个,那么当我们最后选择展示第1个子图时,其实就是展示他本身。
ax.scatter(xcord1, ycord1, s = 30, c = "red", marker = 'x',alpha=0.9)#绘制正样本(用于生成一个scatter散点图)
#s:表示的是大小,是一个标量或者是一个shape大小为(n,)的数组,可选,默认20。
#marker:MarkerStyle,表示的是标记的样式,可选,默认’o’
#alpha:标量(表样本点的亮度),0-1之间,可选,默认None。
ax.scatter(xcord2, ycord2, s =30, c = 'blue',alpha=0.9) #绘制负样本
plt.title('DataSet') #绘制title
plt.xlabel('X1'); plt.ylabel('X2') #绘制label
plt.show() #显示
plotDataSet()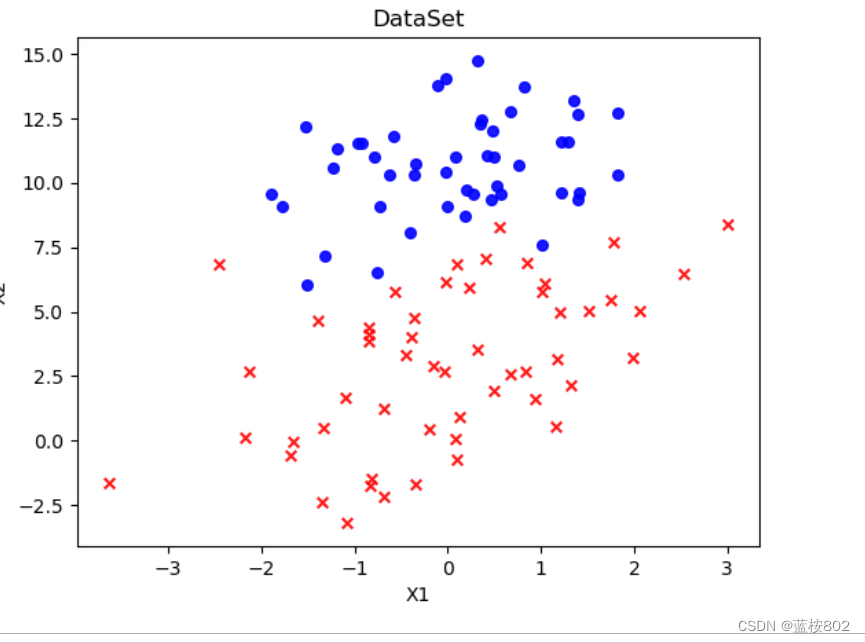
def sigmoid(inX):
sig= 1.0 / (1 + np.exp(-inX))
return sig
def Gradient_Ascent_test():
def f_prime(x_old): #f(x)的导数
return -2 * x_old + 4
x_old = -1 #初始值,给一个小于x_new的值
x_new = 0 #梯度上升算法初始值,即从(0,0)开始
alpha = 0.001 #步长,也就是学习速率,控制更新的幅度
presision = 0.00000001 #精度,也就是更新阈值
while abs(x_new - x_old) > presision:
x_old = x_new
x_new = x_old + alpha * f_prime(x_old) #上面提到的公式
print(x_new) #打印最终求解的极值近似值
Gradient_Ascent_test()
![]()
def gradAscent(dataMatIn, classLabels):
dataMatrix = np.mat(dataMatIn) #转换成numpy的mat(生成矩阵)
labelMat = np.mat(classLabels).transpose() #转换成numpy的mat,并进行转置(行变列)
#区别mat和array,mat可以从字符串或者列表中生成,但是array只能从列表中生成
m, n = np.shape(dataMatrix)#返回dataMatrix的大小。m为行数,n为列数。
alpha = 0.001 #移动步长,也就是学习速率,控制更新的幅度。
maxCycles = 500 #最大迭代次数
weights = np.ones((n,1))
#返回n个数组,每个数组1个元素(上述定义n为列数)
weights_history = []
for k in range(maxCycles):
h= sigmoid(dataMatrix * weights)
error = labelMat - h#是公式里的【y-h0(x)】(labelMat是有0或1的矩阵)
weights = weights + alpha * dataMatrix.transpose() * error # 梯度上升迭代公式
return weights.getA() #将矩阵转换为数组,返回权重数组
if __name__=='__main__':
weights= gradAscent(dataMat,labelMat)
# weights, weights_history = gradAscent(dataMat, labelMat)
print(weights)
def plotBestFit(dataMat, labelMat, weights):
dataMat, labelMat = loadDataSet() #加载数据集,
#将loadDataSet()函数得到的dataMat, labelMat值传到dataMat, labelMat
dataArr = np.array(dataMat) #转换成numpy的array数组
n = np.shape(dataMat)[0] #数据个数,
xcord1 = []; ycord1 = [] #正样本
xcord2 = []; ycord2 = [] #负样本
for i in range(n): #根据数据集标签进行分类
if int(labelMat[i]) == 1:
xcord1.append(dataArr[i,1]); ycord1.append(dataArr[i,2]) #1为正样本
else:
xcord2.append(dataArr[i,1]); ycord2.append(dataArr[i,2]) #0为负样本
fig = plt.figure()
ax = fig.add_subplot(111) #添加subplot
ax.scatter(xcord1, ycord1, s = 30, c = 'red', marker = 'x',alpha=.9)#绘制正样本
#s:表示的是大小,是一个标量或者是一个shape大小为(n,)的数组,可选,默认20。
#marker:MarkerStyle,表示的是标记的样式,可选,默认’o’
#alpha:标量(表样本点的亮度),0-1之间,可选,默认None。
ax.scatter(xcord2, ycord2, s = 30, c = 'blue',alpha=.9) #绘制负样本
x = np.arange(-3.0, 3.0, 0.1)
y = (-weights[0] - weights[1] * x) / weights[2]
ax.plot(x, y)
plt.title('BestFit') #绘制title
plt.xlabel('X1'); plt.ylabel('X2') #绘制label
plt.show()
plotBestFit(dataMat, labelMat, weights)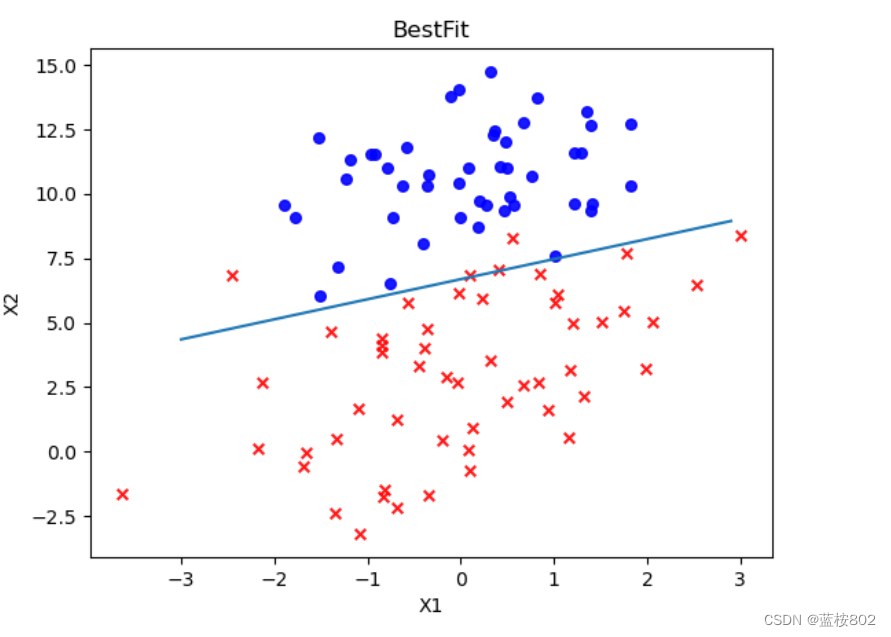
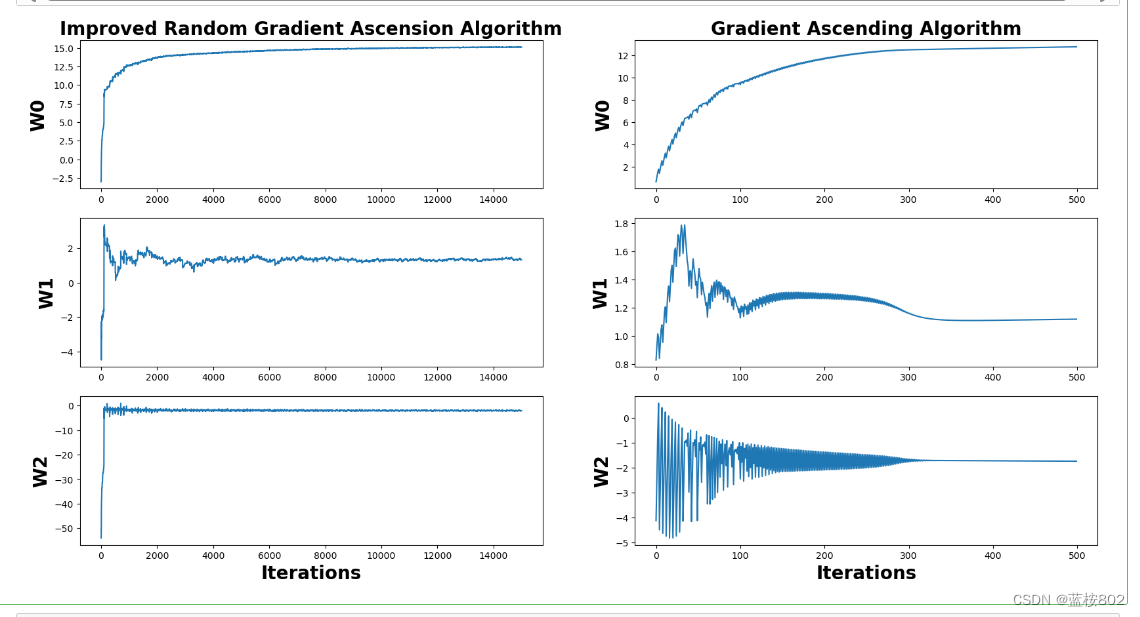
3.logistic,回归系数与迭代次数的关系
# -*- coding:UTF-8 -*-
from matplotlib.font_manager import FontProperties
import matplotlib.pyplot as plt
import numpy as np
import random
def sigmoid(x):
return 1 / (1 + np.exp(-x))
def loadDataSet():
dataMat = []
labelMat = []
fr = open('testSet.txt') # 替换为你的数据文件路径
for line in fr.readlines():
lineArr = line.strip().split()
if len(lineArr) >= 3: # 检查列表长度是否足够
dataMat.append([1.0, float(lineArr[0]), float(lineArr[1])])
labelMat.append(int(lineArr[2]))
else:
print(f"Skipping line with insufficient data: {line.strip()}")
fr.close()
return dataMat, labelMat
"""
函数说明:梯度上升算法
Parameters:
dataMatIn - 数据集
classLabels - 数据标签
Returns:
weights.getA() - 求得的权重数组(最优参数)
weights_array - 每次更新的回归系数
"""
def gradAscent(dataMatIn, classLabels):
dataMatrix = np.mat(dataMatIn) #转换成numpy的mat
labelMat = np.mat(classLabels).transpose() #转换成numpy的mat,并进行转置
m, n = np.shape(dataMatrix) #返回dataMatrix的大小。m为行数,n为列数。
alpha = 0.01 #移动步长,也就是学习速率,控制更新的幅度。
maxCycles = 500 #最大迭代次数
weights = np.ones((n,1))
weights_array = np.array([])
for k in range(maxCycles):
h = sigmoid(dataMatrix * weights) #梯度上升矢量化公式
error = labelMat - h
weights = weights + alpha * dataMatrix.transpose() * error
weights_array = np.append(weights_array,weights)
weights_array = weights_array.reshape(maxCycles,n)
return weights.getA(),weights_array #将矩阵转换为数组,并返回
"""
函数说明:改进的随机梯度上升算法
Parameters:
dataMatrix - 数据数组
classLabels - 数据标签
numIter - 迭代次数
Returns:
weights - 求得的回归系数数组(最优参数)
weights_array - 每次更新的回归系数
"""
def stocGradAscent1(dataMatrix, classLabels, numIter=150):
m,n = np.shape(dataMatrix) #返回dataMatrix的大小。m为行数,n为列数。
weights = np.ones(n) #参数初始化
weights_array = np.array([]) #存储每次更新的回归系数
for j in range(numIter):
dataIndex = list(range(m))
for i in range(m):
alpha = 4/(1.0+j+i)+0.01 #降低alpha的大小,每次减小1/(j+i)。
randIndex = int(random.uniform(0,len(dataIndex))) #随机选取样本
h = sigmoid(sum(dataMatrix[dataIndex[randIndex]]*weights)) #选择随机选取的一个样本,计算h
error = classLabels[dataIndex[randIndex]] - h #计算误差
weights = weights + alpha * error * dataMatrix[dataIndex[randIndex]] #更新回归系数
weights_array = np.append(weights_array,weights,axis=0) #添加回归系数到数组中
del(dataIndex[randIndex]) #删除已经使用的样本
weights_array = weights_array.reshape(numIter*m,n) #改变维度
return weights,weights_array #返回
"""
函数说明:绘制回归系数与迭代次数的关系
Parameters:
weights_array1 - 回归系数数组1
weights_array2 - 回归系数数组2
"""
def plotWeights(weights_array1,weights_array2):
fig, axs = plt.subplots(nrows=3, ncols=2,sharex=False, sharey=False, figsize=(20,10))
x1 = np.arange(0, len(weights_array1), 1)
# 绘制w0与迭代次数的关系
axs[0][0].plot(x1,weights_array1[:,0])
axs0_title_text = axs[0][0].set_title(u'Improved Random Gradient Ascension Algorithm')
axs0_ylabel_text = axs[0][0].set_ylabel(u'W0')
plt.setp(axs0_title_text, size=20, weight='bold', color='black')
plt.setp(axs0_ylabel_text, size=20, weight='bold', color='black')
# 绘制w1与迭代次数的关系
axs[1][0].plot(x1,weights_array1[:,1])
axs1_ylabel_text = axs[1][0].set_ylabel(u'W1')
plt.setp(axs1_ylabel_text, size=20, weight='bold', color='black')
# 绘制w2与迭代次数的关系
axs[2][0].plot(x1,weights_array1[:,2])
axs2_xlabel_text = axs[2][0].set_xlabel(u'Iterations')
axs2_ylabel_text = axs[2][0].set_ylabel(u'W2')
plt.setp(axs2_xlabel_text, size=20, weight='bold', color='black')
plt.setp(axs2_ylabel_text, size=20, weight='bold', color='black')
x2 = np.arange(0, len(weights_array2), 1)
# 绘制w0与迭代次数的关系
axs[0][1].plot(x2,weights_array2[:,0])
axs0_title_text = axs[0][1].set_title(u'Gradient Ascending Algorithm')
axs0_ylabel_text = axs[0][1].set_ylabel(u'W0')
plt.setp(axs0_title_text, size=20, weight='bold', color='black')
plt.setp(axs0_ylabel_text, size=20, weight='bold', color='black')
# 绘制w1与迭代次数的关系
axs[1][1].plot(x2,weights_array2[:,1])
axs1_ylabel_text = axs[1][1].set_ylabel(u'W1')
plt.setp(axs1_ylabel_text, size=20, weight='bold', color='black')
# 绘制w2与迭代次数的关系
axs[2][1].plot(x2,weights_array2[:,2])
axs2_xlabel_text = axs[2][1].set_xlabel(u'Iterations')
axs2_ylabel_text = axs[2][1].set_ylabel(u'W2')
plt.setp(axs2_xlabel_text, size=20, weight='bold', color='black')
plt.setp(axs2_ylabel_text, size=20, weight='bold', color='black')
plt.show()
if __name__ == '__main__':
dataMat, labelMat = loadDataSet()
weights1,weights_array1 = stocGradAscent1(np.array(dataMat), labelMat)
weights2,weights_array2 = gradAscent(dataMat, labelMat)
plotWeights(weights_array1, weights_array2)