张量Tensor

张量(Tensor)基础
张量是MindSpore中的基本数据结构的一种,类似于NumPy中数组和矩阵非常相似。它具有以下重要属性:
- 形状(shape)和数据类型(dtype):每个张量都有确定的形状和数据类型,这决定了它在计算中的用途和行为。
- 创建方法:可以通过直接传入数据、从NumPy数组生成、使用初始化器(如One、Normal)或者从其他张量继承属性来创建张量。
- 索引和切片:类似于NumPy,张量支持方便的索引和切片操作,允许按需访问和操作数据元素。
- 运算:支持各种张量之间的数学运算,如加减乘除、取模、整除等,操作与NumPy类似。
import numpy as np
import mindspore
from mindspore import ops
from mindspore import Tensor, CSRTensor, COOTensor
创建张量
张量的创建方式有多种,构造张量时,支持传入Tensor、float、int、bool、tuple、list和numpy.ndarray类型。
-
根据数据直接生成
可以根据数据创建张量,数据类型可以设置或者通过框架自动推断。data = [1, 0, 1, 0] x_data = Tensor(data) print(x_data, x_data.shape, x_data.dtype)代码执行结果:[1 0 1 0] (4,) Int64
-
从NumPy数组生成
可以从NumPy数组创建张量。np_array = np.array(data) x_np = Tensor(np_array) print(x_np, x_np.shape, x_np.dtype)[1 0 1 0] (4,) Int64
-
使用init初始化器构造张量
当使用init初始化器对张量进行初始化时,支持传入的参数有init、shape、dtype。- init: 支持传入initializer的子类。如:下方示例中的 One() 和 Normal()。
- shape: 支持传入 list、tuple、 int。
- dtype: 支持传入mindspore.dtype。
from mindspore.common.initializer import One, Normal # Initialize a tensor with ones tensor1 = mindspore.Tensor(shape=(2, 2), dtype=mindspore.float32, init=One()) # Initialize a tensor from normal distribution tensor2 = mindspore.Tensor(shape=(2, 2), dtype=mindspore.float32, init=Normal()) print("tensor1:\n", tensor1) print("tensor2:\n", tensor2)tensor1:
[[1. 1.]
[1. 1.]]
tensor2:
[[-0.00063482 -0.00916224]
[ 0.01324238 -0.0171206 ]] -
继承另一个张量的属性,形成新的张量
from mindspore import ops x_ones = ops.ones_like(x_data) print(f"Ones Tensor: \n {x_ones} \n") x_zeros = ops.zeros_like(x_data) print(f"Zeros Tensor: \n {x_zeros} \n")Ones Tensor:
[1 1 1 1]
Zeros Tensor:
[0 0 0 0]
张量的属性
张量的属性包括形状、数据类型、转置张量、单个元素大小、占用字节数量、维数、元素个数和每一维步长。
-
形状(shape):Tensor的shape,是一个tuple。
-
数据类型(dtype):Tensor的dtype,是MindSpore的一个数据类型。
-
单个元素大小(itemsize): Tensor中每一个元素占用字节数,是一个整数。
-
占用字节数量(nbytes): Tensor占用的总字节数,是一个整数。
-
维数(ndim): Tensor的秩,也就是len(tensor.shape),是一个整数。
-
元素个数(size): Tensor中所有元素的个数,是一个整数。
-
每一维步长(strides): Tensor每一维所需要的字节数,是一个tuple。
x = Tensor(np.array([[1, 2], [3, 4]]), mindspore.int32)
print("x_shape:", x.shape)
print("x_dtype:", x.dtype)
print("x_itemsize:", x.itemsize)
print("x_nbytes:", x.nbytes)
print("x_ndim:", x.ndim)
print("x_size:", x.size)
print("x_strides:", x.strides)

张量索引
Tensor索引与Numpy索引类似,索引从0开始编制,负索引表示按倒序编制,冒号:和 …用于对数据进行切片。
tensor = Tensor(np.array([[0, 1], [2, 3]]).astype(np.float32))
print("First row: {}".format(tensor[0]))
print("value of bottom right corner: {}".format(tensor[1, 1]))
print("Last column: {}".format(tensor[:, -1]))
print("First column: {}".format(tensor[..., 0]))
First row: [0. 1.]
value of bottom right corner: 3.0
Last column: [1.3.]
First column: [0. 2.]
张量运算
张量之间有很多运算,包括算术、线性代数、矩阵处理(转置、标引、切片)、采样等,张量运算和NumPy的使用方式类似,下面介绍其中几种操作。
普通算术运算有:加(+)、减(-)、乘(*)、除(/)、取模(%)、整除(//)。
x = Tensor(np.array([1, 2, 3]), mindspore.float32)
y = Tensor(np.array([4, 5, 6]), mindspore.float32)
output_add = x + y
output_sub = x - y
output_mul = x * y
output_div = y / x
output_mod = y % x
output_floordiv = y // x
print("add:", output_add)
print("sub:", output_sub)
print("mul:", output_mul)
print("div:", output_div)
print("mod:", output_mod)
print("floordiv:", output_floordiv)
add: [5. 7. 9.]
sub: [-3. -3. -3.]
mul: [ 4. 10. 18.]
div: [4. 2.5 2.]
mod: [0. 1. 0.]
floordiv: [4. 2. 2.]
concat将给定维度上的一系列张量连接起来。
data1 = Tensor(np.array([[0, 1], [2, 3]]).astype(np.float32))
data2 = Tensor(np.array([[4, 5], [6, 7]]).astype(np.float32))
output = ops.concat((data1, data2), axis=0)
print(output)
print("shape:\n", output.shape)
[[0. 1.] [2. 3.] [4. 5.] [6. 7.]] shape: (4, 2)
stack则是从另一个维度上将两个张量合并起来。
data1 = Tensor(np.array([[0, 1], [2, 3]]).astype(np.float32))
data2 = Tensor(np.array([[4, 5], [6, 7]]).astype(np.float32))
output = ops.stack([data1, data2])
print(output)
print("shape:\n", output.shape)
[[[0. 1.] [2. 3.]]
[[4. 5.] [6. 7.]]] shape: (2, 2, 2)
Tensor与NumPy转换
Tensor可以和NumPy进行互相转换。
Tensor转换为NumPy
与张量创建相同,使用 Tensor.asnumpy() 将Tensor变量转换为NumPy变量。
t = Tensor([1., 1., 1., 1., 1.])
print(f"t: {t}", type(t))
n = t.asnumpy()
print(f"n: {n}", type(n))
t: [1. 1. 1. 1. 1.] <class ‘mindspore.common.tensor.Tensor’> n: [1. 1.
- 1.] <class ‘numpy.ndarray’>
NumPy转换为Tensor
使用Tensor()将NumPy变量转换为Tensor变量。
n = np.ones(5)
t = Tensor.from_numpy(n)
np.add(n, 1, out=n)
print(f"n: {n}", type(n))
print(f"t: {t}", type(t))
n: [2. 2. 2. 2. 2.] <class ‘numpy.ndarray’> t: [2. 2. 2. 2. 2.] <class
‘mindspore.common.tensor.Tensor’>
稀疏张量(Sparse Tensor)
稀疏张量是一种优化的数据结构,适用于大部分元素为零的情况,特别是在推荐系统、图神经网络等应用中有重要应用:
- CSR稀疏张量:采用压缩稀疏行(CSR)格式存储数据,通过indptr、indices和values表示非零元素的位置和值。
- COO稀疏张量:采用坐标格式(COO)存储数据,通过indices和values表示非零元素的位置和值,适合表示稀疏的多维数据。

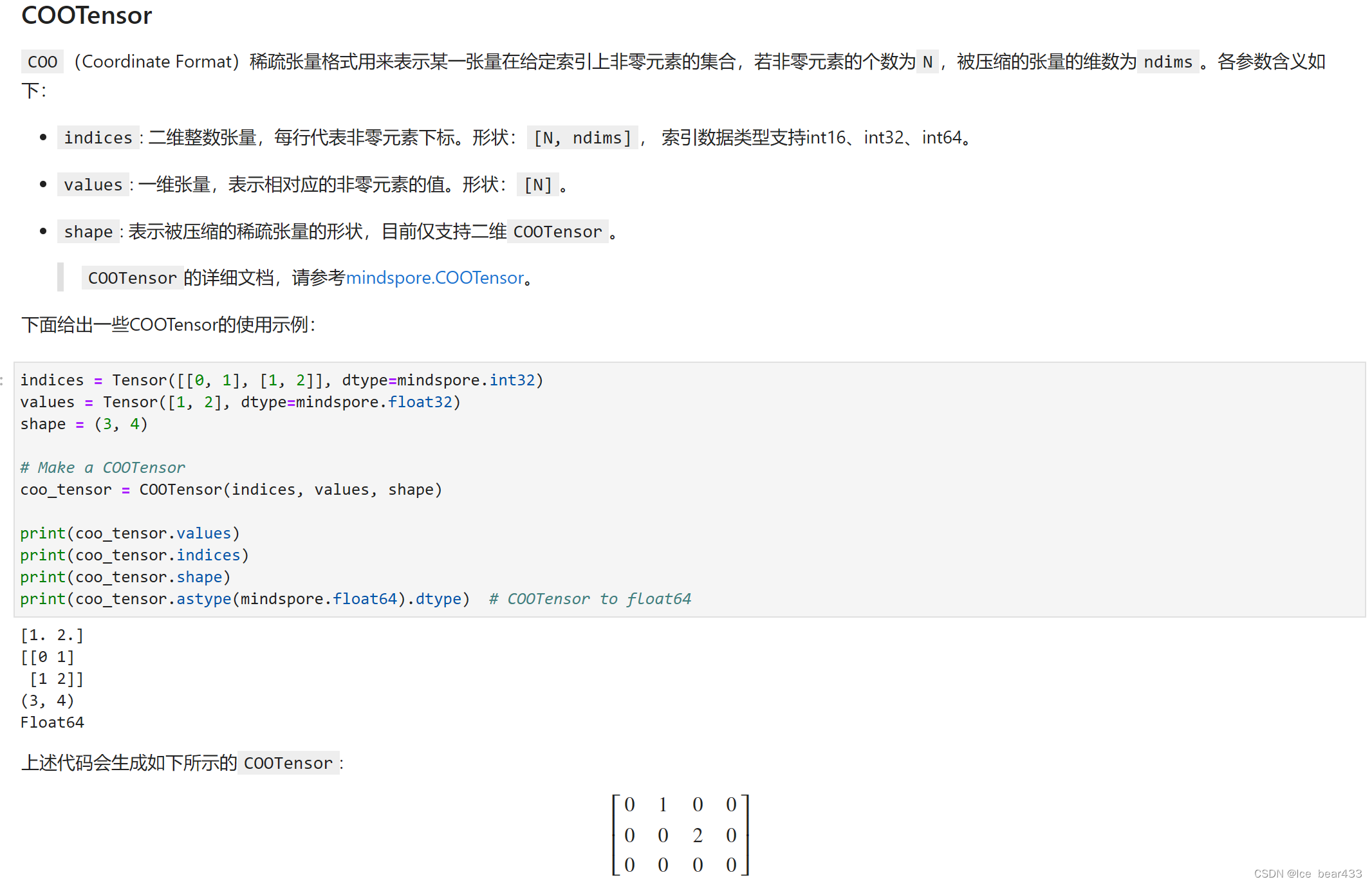
通过学习MindSpore中的张量和稀疏张量,我深入了解了如何有效地管理和操作大规模数据,以及如何利用稀疏数据结构来提升计算效率和节省存储空间。