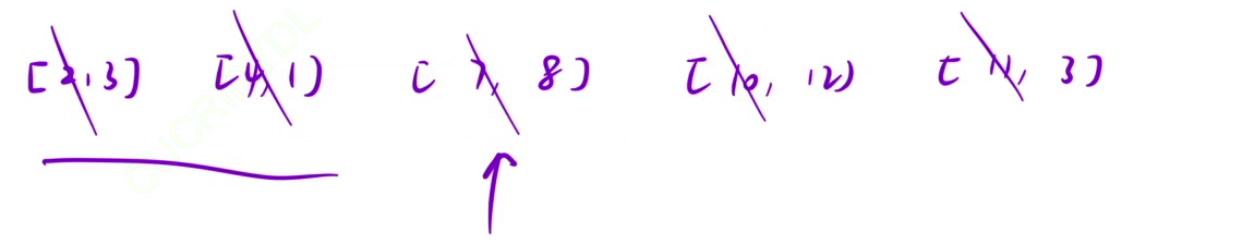0、贪心算法介绍





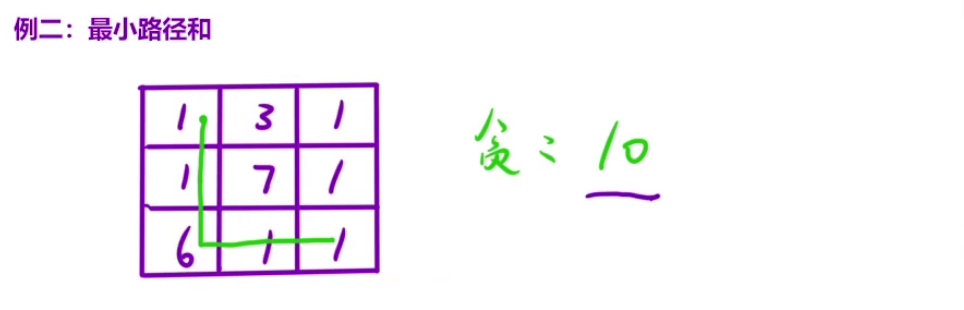

例三中的最优解为装两个2号物品,总价值为14。贪心算法+鼠目寸光

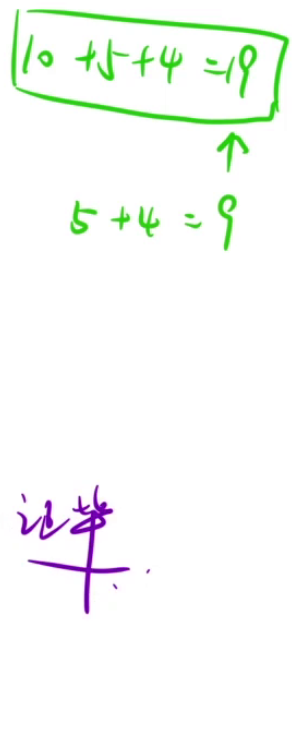
解释:若某个位置的最优解为20元,那么10元的就一定不超过一张,否则两张10元就可以被一张20元代替,同理5元的最大张数为1,1元的最大张数为4。
贪心:[20x1,10x2,5x3,1x4];最优解:[20y1,10y2,5y3,1y4]。若a比A多一张,那么就需要后面的面额凑出来一张a,根据上述的性质,这是不可能的,所以x1一定不大于y1。x1不可能小于y1,若20元纸币可以去y1张,那么根据贪心策略x1一定大于等于y1。综上所述,x1只可能等于y1。以此类推,x2y2,x3y3,x4==y4。所以找零钱使用贪心策略找到的一定是最优解·。
1、柠檬水找零

class Solution {
public boolean lemonadeChange(int[] bills) {
// 0、仅有三个面额,20美元的纸币不会被用
int five = 0, ten = 0;
for(int x:bills){
// 1、分类讨论
// 1.1、遇见5直接收下
if(x==5){
five++;
}else if(x == 10){
// 1.2、遇见10收下,找出一张5美元
five--;
ten++;
}else {
// 1.3、遇见20美元,贪心的现有10美元找了,再用5美元找零
if(ten>0&&five>0){
ten--;five--;
} else {
five-=3;
}
}
// 2、尝试找零后的结果非法,那么就是找不开,返回false
if(five<0 || ten<0){
return false;
}
}
return true;
}
}

有点抽象!!!
**贪心策略:**收到20美元需要找零15美元可以使用[5,10]组合或者[5,5,5];收到10美元的时候需要找零5美元;可见5美元的作用很大既可以用于找零20美元,也可以用于找零10美元,所以我的贪心策略找零时尽量先使用10美元,尽量节省5美元的时候,若提前把5美用光了,那么后面需要用五美元的时候10美元起不了作用。
贪心策略的正确性:(交换论证法)假设每次找零的情况为:[5,5,5] , [5] , [10] , [10]
可见前期某一次使用两张5美元找零代替了一张10美元,显然可以将后面某次使用10美元找零与本次使用两张5美元交换,即[5,10] , [5] , [10] , [5,5],也就是说最优解可以通过交换转化为贪心解。
2、将数组和减半的最小操作次数

class Solution {
public int halveArray(int[] nums) {
// 0、贪心策略:每次都让数组中最大的数减半
double sum=0;
PriorityQueue<Double> queue = new PriorityQueue<>((a, b) -> Double.compare(b, a));
for(int num : nums){
sum+=num;
queue.add((double)num);
}
sum/=2;
int step=0;
double deincrice=0;
while(deincrice<sum){
step++;
double max = queue.poll()/2;
deincrice+=max;
queue.add(max);
}
return step;
}
}
贪心策略:每次都将数组中最大的那个值减半,这样操作的次数就是最小操作数。
贪心策略的正确性:(交换论证法),对于某个最优解每次减半的数字为(a<b<c<d)经过四次减半操作后数组和降至原来的一半,那么对于贪心解(d>c>b>a)经过四次数字减半后数组和也一定降至了原来的一半。通过交换被减半数字的位置,最优解可以调整为贪心解。
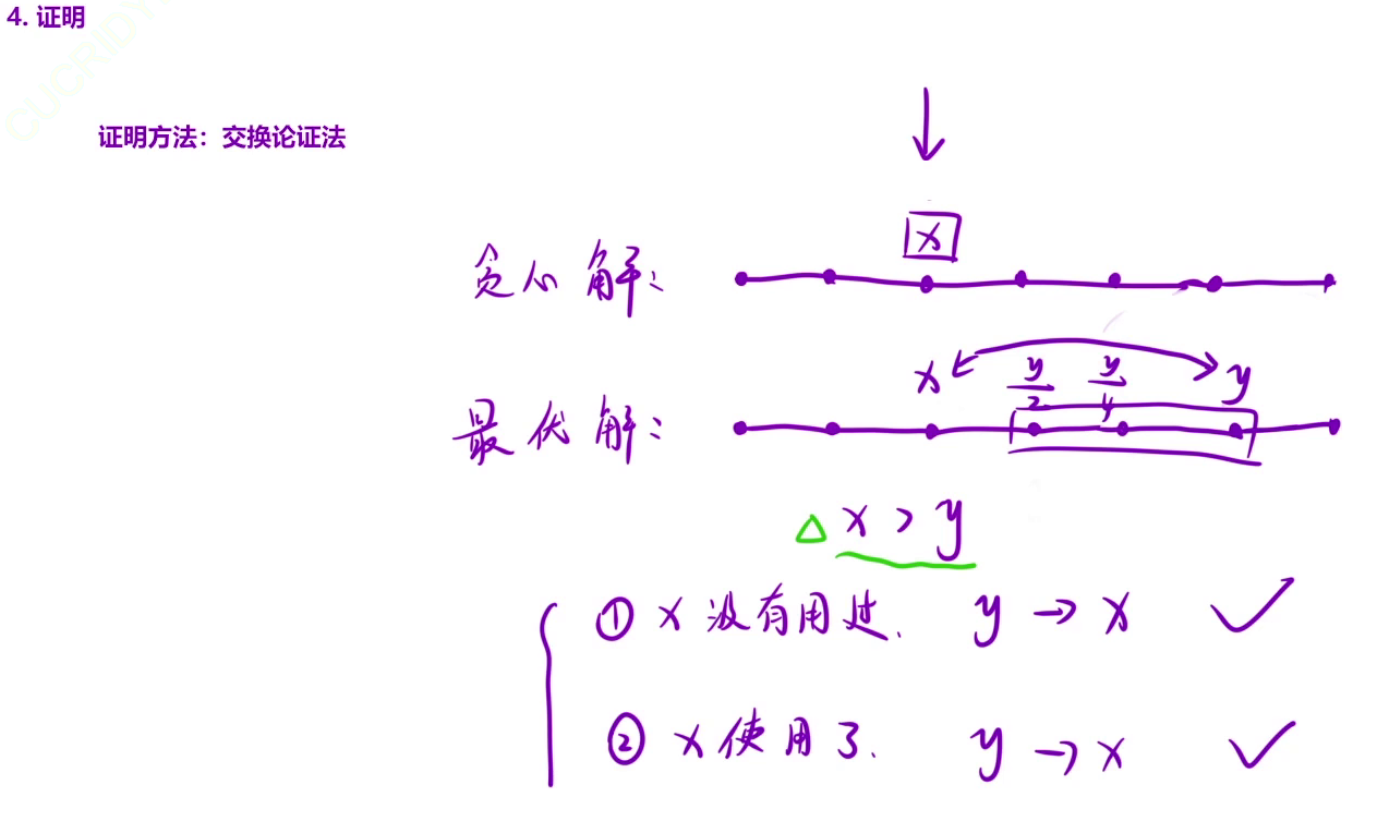
**什么是最优解:**就是复合题意的解,可能不止一个,且包含贪心解,贪心解往往只有一个,若所有最优解都与贪心解等价,通过变换可以变成贪心解,那么这个贪心策略就是可行的
3、最大数 ★★★★

class Solution {
public String largestNumber(int[] nums) {
// 0、贪心策略:最高位越大、越靠前
// 1、类似于字符串根据字典序排序一样,对nums进行排序,而不是按照大小排序
int n = nums.length;
String[] strs = new String[n];
for(int i=0;i<n;i++) strs[i] = "" + nums[i];
// 排序
Arrays.sort(strs,(a,b)->{
// 这个排序的规则才是最细节的地方
return (b+a).compareTo(a+b);
});
StringBuffer ret = new StringBuffer();
for(String s : strs) ret.append(s);
if(ret.charAt(0)=='0') return "0";
return ret.toString();
}
}
这个题目要举几个例子充分理解题目;
若排序采用:return (b+a).compareTo(a+b); 根据数字的字典序进行倒序,如果(b+a)>(a+b),那么b一定要安排在a的前面;又有(c+a)>(c+b),(b+c)>(c+b),则最后的排序就是 bca 。
排序前:nums = [1,2,3,4,5,6,7,8,9,0,10]
排序后:strs = [9,8,7,6,5,4,3,2,1,10,0]
最大数:“987654321100”结果正确
若排序采用:return (b).compareTo(a); 根据数字的字典序进行倒序,这种排序策略看似可行实则不行
排序前:nums:[3,30,34,5,9]
排序后:strs:[“9”,“5”,“34”,“30”,“3”]
最大值:“9534303” 结果错误
回顾时所写:
首先,因为设计到数字的拼接所以将数字转化为字符串更为方便
其次就是这个题目的贪心策略:根据字典序排序则有:“abc”<“ab”,“90”<“9”


a>=b && a<=b ,由夹逼准则可得a==b
4、摆动序列 ★★★★★★


贪心策略:遍历数组[1,3,5,4,2,6,8,7]。遍历到3时,摆动数组是[1,3]。遍历到5时,摆动数组是[1,3]还是[1,5]呢?发动你贪婪的心,摆动数组应该是[1,5],因为若后面的元素小于5摆动数组就会变长,但后面的元素不一定小于3摆动数组长度不变;相反,如果数组成递减趋势[1,5,4]和[1,5,2],贪心策略会上我们选择[1,5,2];
分析完贪心策略,可以明显发现其实就是统计波峰与波谷的数量。
回顾时补写:
即使没有贪心的想法也可以看出这个题目就是在统计波峰波谷的数量,这样一写题目的思路就是围绕着波峰波谷,方法忽悠很多,我和吴老师写的就不太一样;
如果使用贪心策略的想法写代码就因该创建出一个链表存储摆动序列,一边遍历数组,一边维护摆动序列,根据上述的贪心策略,最后的摆动序列会变成波峰波谷的集合。因为是在摆动的时候统计摆动数组的长度,因此也只是关注链表的最后一个元素,所以也没必要创建一个链表。
class Solution {
public int wiggleMaxLength(int[] nums) {
int n = nums.length;
if(n==1) return 1;
int slope = 0; // 斜率,无所谓可以初始化为1或者-1
Stack<Integer> wobble = new Stack<>();// 摆动序列wobble sequence
wobble.push(nums[0]);
int step = 0;
for (int i = 1; i < n; i++) {
if (wobble.peek() != nums[i]) {
int temp = nums[i]-wobble.peek();
if(slope*temp<=0) {
step++;
wobble.push(nums[i]);
slope = temp;
}else{
wobble.pop();
wobble.push(nums[i]);
}
}
}
return step + 1;
}
}
摆动暴动序列的特殊情况还挺多的,好难
class Solution {
public int wiggleMaxLength(int[] nums) {
// 返回最长子序列而不是子数组
int n = nums.length;
if (n == 1)
return 1;
int direction = 0;// 代表斜率,等于1或者-1
int step = 1;// 步数
int i = 0; //遍历数组
// 例如:5552637
// 这段while循环就是为了遍历到开头平底的最后一个位置
while (i + 1 < n) {
if (nums[i] == nums[i + 1]) { // 平地则不考虑
i++;
} else {
// 维护斜率
direction = nums[i] < nums[i + 1] ? 1 : -1;
step++;
break;
}
}
// 继续遍历数组,每一次斜率变化进行步数加1
for (i++; i + 1 < n; i++) {
if (nums[i] != nums[i + 1]) {
int temp = 0;
temp = nums[i] < nums[i + 1] ? 1 : -1;
if (direction != temp) {
direction = temp;
step++;
}
}
}
return step;
}
}
class Solution {
public int wiggleMaxLength(int[] nums) {
int n = nums.length;
if (n < 2)
return n;
int ret = 0, left = 0;
for (int i = 0; i < n - 1; i++) {
// 如果⽔平,直接跳过
if (nums[i + 1] != nums[i]){
int right = nums[i + 1] - nums[i]; // 计算接下来的趋势
if (left * right <= 0){
ret++; // 累加波峰或者波⾕
}
left = right;
}
}
return ret + 1;
}
}
两代码意思是一样的,但是我没能把特殊情况于普通情况合并处理,导致用了很多变量。
贪心策略可行性证明:

5、最长递增子序列★★★★★

贪心策略:
为什么这个贪心策略是对的?
ArrayList ret 中第 i 个结点存储的是 【长度为i+1递增子序列的末尾的最小值】
这跟贪心策略有关系吗?什么是贪心?就是鼠目寸光的认为局部最优解就是全局最优解啊!
数组[7,3,8,4,7,2,14,13]进行遍历:
cur=7:此时只有一个元素,[7]是唯一的递增子序列,长度为1。ret.add(7);ret.size()==1,代表当前最大子序列的长度为1;ret=[7];
**cur=3:**3比7小,不与7给构成递增子序列。此时就有两个长度为1的递增子序列[3],[7]。但实际上只需要关注[3]即可,因为如果后续有数字可以与[7]构成长度位的递增子序列,那么也一定可以与[3]构成递增子序列。ret=[3];
**cur=8:**因为8>4,可以与[3]构成长度为2的递增子序列,ret.add(8);ret.size()==2,代表当前最大子序列的长度为2;ret=[3,8];
**cur=4:**先更新长度为1的递增子序列末尾的最小值,4>3所以不能更新。再看看长度为2的递增子序列的末尾的最小值是否可以更新,因为4<8,[3,4]和[3,8]这两个长度为2的第增子序列,如果后面有数字可以与[3,8]构成长度为3的子序列,那么也一定能与[3,4]构成长度为3的递增子序列,反之则不一定。所以仅关注这两个子序列末尾值小的那个即可,更新长度为2的递增子序列的末尾的最小值为4;
ret=[3,4];
**cur=7:**显然7大于ret的尾结点,所以可以构成长度为3的递增子序列,此时ret.add(7),ret=[3,4,7].
**cur=2:**以此与ret[i]进行比较,2可以更新长度为1的递增子序列的末尾的最小值,ret=[2,4,7];
**cur=14:**更新ret长度,ret.add(14).ret=[2,4,7,14];
cur=13:更新长度为此的递增子序列的末尾的最小值,ret=[2,4,7,13];
一趟下来以后我们找到了每一种长度递增子序列的末尾的最小值,那么最长递增子序列的长度就是有多少中最长递增子序列(第一种长度为1,第二种长度为2,第n种长度为n,n最长,所以种类数等于最大长度),也就是ret.size()
贪心体现在我只需要关心每一种递增子序列中那个末尾值最小的子序列即可,上述模拟过程中的任何一个位置ret.size()都是局部最优解。
PS:最后的ret数组不是一个最长递增子序列,不要产生错觉,因我们全程的目的并不是找到一个最长递增子序列。
**优化:**遍历数组nums是O(N),存入 nums[i]到ret中是O(N)的,整体时间复杂度为O(N^2),因为ret是递增的(根据链表构造是的条件可证),所以可以使用二分插入,将时间复杂度优化到O(logN),整体的时间复杂度为O(NlogN)。
class Solution {
public int lengthOfLIS(int[] nums) {
ArrayList<Integer> ret = new ArrayList<>();
int n = nums.length;
ret.add(nums[0]);
for (int i = 1; i < n; i++) {
if (nums[i] > ret.get(ret.size() - 1)) // 如果能接在最后⼀个元素后⾯,直接放
{
ret.add(nums[i]);
} else {
// ⼆分插⼊位置
int left = 0, right = ret.size() - 1;
while (left < right) {
int mid = (left + right) / 2;
if (ret.get(mid) < nums[i])
left = mid + 1;
else
right = mid;
}
ret.set(left, nums[i]); // 放在 left 位置上
}
}
return ret.size();
}
}
class Solution {
public int lengthOfLIS(int[] nums) {
int n = nums.length;
int[] dp = new int[n+1];
int ret = 0;
for(int i=1;i<=n;i++){
for(int j=1;j<i;j++){
if(nums[i-1]>nums[j-1]){
dp[i] = Math.max(dp[i],dp[j]);
}
}
dp[i] += 1;
ret = Math.max(ret,dp[i]);
}
return ret;
}
}
// 时间复杂度O(N^2)
6、递增的三元子序列★★★★★


这一题比上一题简单,我们只需要证明有三元组(长度为三的递增子序列)即可,因为长度仅为3,可以使用两个变量来代替ret数组,更新这两个变量时(也就是更新ret时)只需两次比较即可,不用二分优化了,所以整体的时间复杂度为O(2N);
class Solution {
public boolean increasingTriplet(int[] nums) {
int n = nums.length;
int a = nums[0], b = Integer.MAX_VALUE;
for (int i = 1; i < n; i++) {
if (nums[i] < a) // 如果能接在最后⼀个元素后⾯,直接放
{
a = nums[i];
} else if (b < nums[i]) {
return true;
} else {
b = nums[i];
}
}
return false;
}
}
7、最长连续递增序列

class Solution {
public int findLengthOfLCIS(int[] nums) {
// 双指针
int n = nums.length;
int left = 0, right = 1;
int max = 1;
while(right<n){
if(nums[right]>nums[right-1]){
right++;
max = Math.max(max,right-left);
}else{
left=right;
right++;
}
}
return max;
}
}
双指针算法,双指针遍历可以回退,也可以不回退(为什么可以不会退呢,回退是因为从i位置遍历到此处连续递增序列发生了终断,即使回退到i+1位置重新遍历到此处也还是终断,因此没必要),贪心的策略就是不回退。双指针遍历到任意位置,max的值都是当前最优解,当双指针遍历完整个数组,max也是全局最优解。
没必要把这个题目强行理解为贪心算法,
8、买卖股票的最佳时机

class Solution {
int[] temp;
public int maxProfit(int[] prices) {
// 二分法
int n = prices.length;
temp = new int[n];
return mergeSort(prices,0,n-1);
}
public int mergeSort(int[] prices ,int left,int right){
if(left>=right) return 0;
int mid = left + (right - left)/2;
// 0、归并排序求最大差值
int max_left = mergeSort(prices,left,mid);
int max_right = mergeSort(prices,mid+1,right);
int max = Math.max(max_left,max_right);
// 1、返回值,三者的最大值
max = Math.max(max,prices[right]-prices[left]);
// 排序
int i=left,j=mid+1,k=0;
while(i<=mid && j<=right){
if(prices[i] < prices[j]){
temp[k++] = prices[i++];
}else{
temp[k++] = prices[j++];
}
}
while(i<=mid){
temp[k++] = prices[i++];
}
while(j<=right){
temp[k++] = prices[j++];
}
for(k=0;k<right-left+1;k++){
prices[k+left] = temp[k];
}
return max;
}
}
// 时间复杂度:// O(NLogN)
class Solution {
int[] temp;
public int maxProfit(int[] prices) {
// 二分法
int n = prices.length;
PriorityQueue<Integer> maxHeap = new PriorityQueue<>((a, b) -> b - a);
maxHeap.add(prices[0]);
int max = 0;
for (int i = 1; i < n; i++) {
max = Math.max(max, prices[i] - maxHeap.peek());
maxHeap.add(prices[i]);
maxHeap.poll();
}
return max;
}
}
// 小根堆也可以,但是小根堆会存储prices的所有元素,没必要
// 保持大根堆的大小为1即可
// 时间复杂度:O(Nlogn),比分治优化了一点
// 使用小根堆的解法时间复杂度也是O(NlogN)
class Solution {
public int maxProfit(int[] prices) {
// 贪心贪的不明显
int n = prices.length;
int min = prices[0];
int max = 0;
for (int i = 1; i < n; i++) {
max = Math.max(max, prices[i] - min); // 先更新最大收益
min = Math.min(min,prices[i]); // 再更新最低价
}
return max;
}
}
// 没必要使用大根堆,使用一个变量去记录前驱的最小值即可。
// 时间复杂度为O(N)
遍历股价,min记录当前股价最低值,可初始化为第一天的价格。max记录最高差价,用当天的价格减去以往的最低价格去比较历史最该差价。注意是以往最低价,所以这题不是求最大值最小值的差。
该题目是只能买卖一次,且不能在同一天买卖。
// 动态规划也能解决
9、买卖股票的最佳时机II

class Solution {
public int maxProfit(int[] prices) {
// 可以买卖多次
// 只要明天比今天股价高,那么就进行一次今天买,明天卖,每一次利润都争取
int max = 0;
int i = 0, j = 0, n = prices.length;
while (j < n - 1) {
if (prices[j] < prices[j+1]) {
max += prices[j+1] - prices[j];
}
j++;
}
return max;
}
}
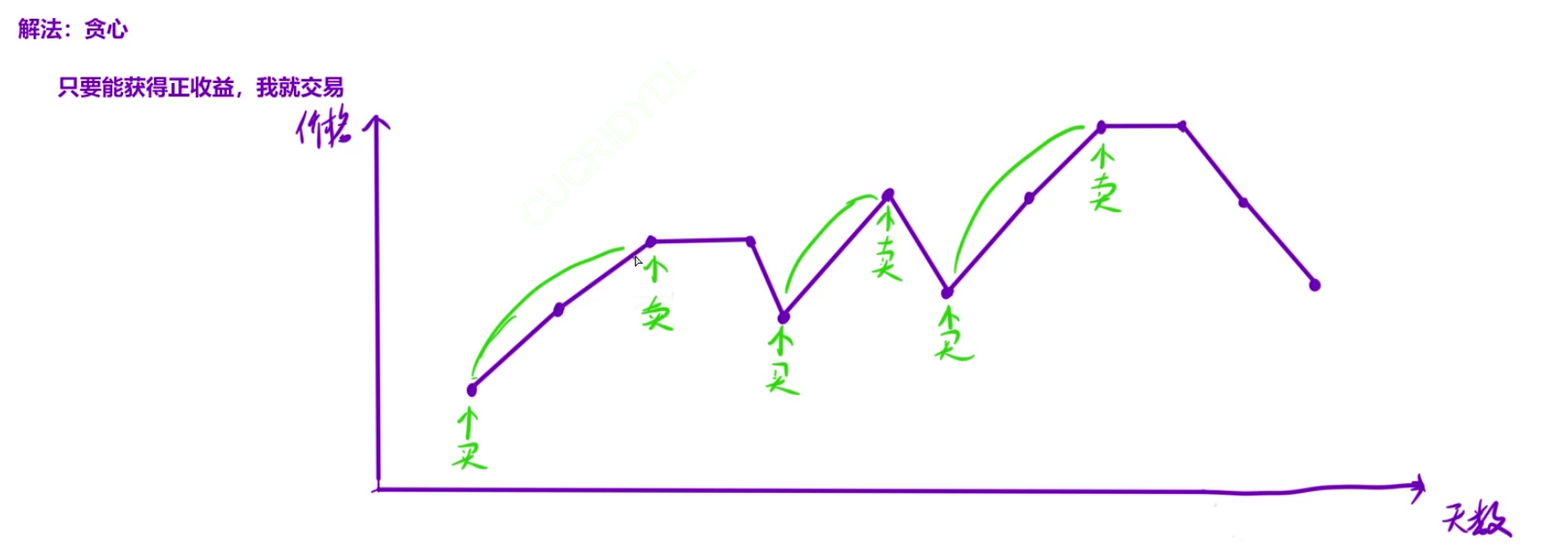
**贪心策略:**只要明天比今天股价高,我就进行买卖。并不考虑等股价上升到最高点再进行买卖。
10、k次取反后最大化的数组和

class Solution {
public int largestSumAfterKNegations(int[] nums, int k) {
// 遇见负数就取反
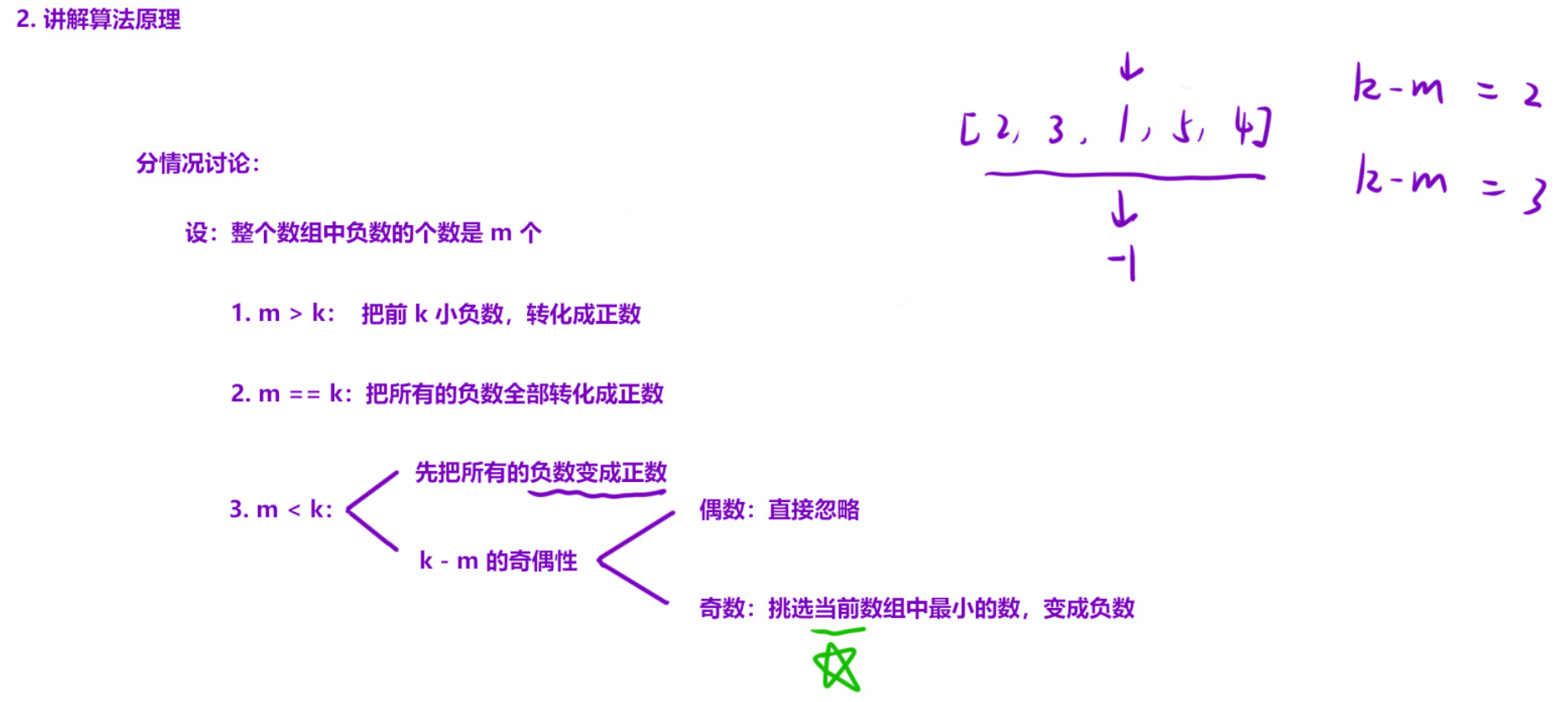
// 情况好多,一趟遍历搞不定,艹,不是我无能。
int m = 0, minElem = Integer.MAX_VALUE, n = nums.length;
for (int x : nums) {
if (x < 0)
m++;
minElem = Math.min(minElem, Math.abs(x));
}
// 分类讨论
int ret = 0;
if (m > k) {
Arrays.sort(nums);
for (int i = 0; i < k; i++) // 前 k ⼩个负数,变成正数
{
ret += -nums[i];
}
for (int i = k; i < n; i++) // 后⾯的数不变
{
ret += nums[i];
}
} else {
// 把负数全部变成正数
for (int x : nums)
ret += Math.abs(x);
if ((k - m) % 2 != 0) // 判断是否处理最⼩的正数
{
ret -= minElem * 2;
}
}
return ret;
// 为什么一趟遍历搞不定呢?
}
}
回顾时补写:
我一开始想要再一次遍历过程中完成,如果不提前遍历一次,就意味这我并不能提前知道整个数组有多少个负数 ,先排序,然后一边遍历一遍翻转的时候,我可能需要记录我反转哪些元素,以及反转过的最小元素是哪个等等很复杂,一开始写的时候就只想着试试看看,越写越不对劲。最后只能看题解,也没想过这题分类讨论会这么简单。
11、按身高排序 ★★

class Solution {
public String[] sortPeople(String[] names, int[] heights) {
// 1. 创建⼀个下标数组
int n = names.length;
Integer[] index = new Integer[n];
for (int i = 0; i < n; i++)
index[i] = i;
// 2. 对下标数组排序
Arrays.sort(index, (i, j) -> {
return heights[j] - heights[i];
});
// 3. 提取结果
String[] ret = new String[n];
for (int i = 0; i < n; i++) {
ret[i] = names[index[i]];
}
return ret;
}
}
本题主要书介绍了下标数组,不改变原数组的情况下,对下标数组进行排序,实现从小到大遍历原数组
nums=[8,4,32,16];
index=[0,1,2,3];
对以nums数组对下标数组index进行排序:index’=[1,0,3,2];
通过index’来从小到大访问nums数组:for(int i=0;i<n;i++){ nums[index[i]] };
12、优势洗牌(田忌赛马)

class Solution {
public int[] advantageCount(int[] nums1, int[] nums2) {
int n = nums1.length;
// 0、创建下标数组
Integer[] index2 = new Integer[n];
// 0.1、初始化下标数组
for(int i=0;i<n;i++) index2[i]=i;
Arrays.sort(nums1);
Arrays.sort(index2, (i, j) -> {
return nums2[i] - nums2[j];
});
int[] ret = new int[n];
int i=0;
int left=0,right=n-1;
while(left<=right){ // 或者写成 i<n
if(nums1[i] > nums2[index2[left]]){
// 贪心策略:出最小的大于nums2的数
ret[index2[left++]] = nums1[i++];
}else{
// 贪心策略:下等马消耗上等马
ret[index2[right--]] = nums1[i++];
}
}
return ret;
}
}
// 2 7 11 15 排序的nums1
// 1 10 4 11 //nums2
// 0 2 1 3 //index2
// 8 12 24 32
// 11 13 25 32
回顾时补写:
**赛马的策略:**用劣等马去消耗对方的上等马,每次仅用比对方数值大一点的数值进行匹配。看代码吧,不罗嗦了。
**如何返回复合题目意思的数组:**利用下标数组
两个数组nums1,nums2,调整nums1元素的顺序使其对nums2的优势最大化,用劣等马去消耗对方的上等马,每次仅用比对方数值大一点的数值进行匹配。
例:nums1 = [12,24,8,32], nums2 = [13,25,32,11]
对两个数组进行排序:nums1=[8 ,12,24,32],
nums2=[11,13,25,32]
对两个数组排序后可以显然看出 12对11,24对13,32对25,8对32 就是优势最大化的排列方式
temp[12,24,32,8]对nums2[11,13,25,32];
还原nums2到排序前的顺序,temp同步移动元素得到最终ret=[24,32,8,12]
可以看出实际上并不需要对nums2进行排序,因为还要还原,创建nums2的下标数组index2,根据nums[index2[i]] 可以锁定nums排序后的第i个元素。在构造ret[]的时候使用ret[index2[i]]直接nums1元素该放在那个位置。(i:使用i遍历排序后的nums1,以为nums1排序后方便使用贪心策略,每回合出最小的比nums2大的元素)
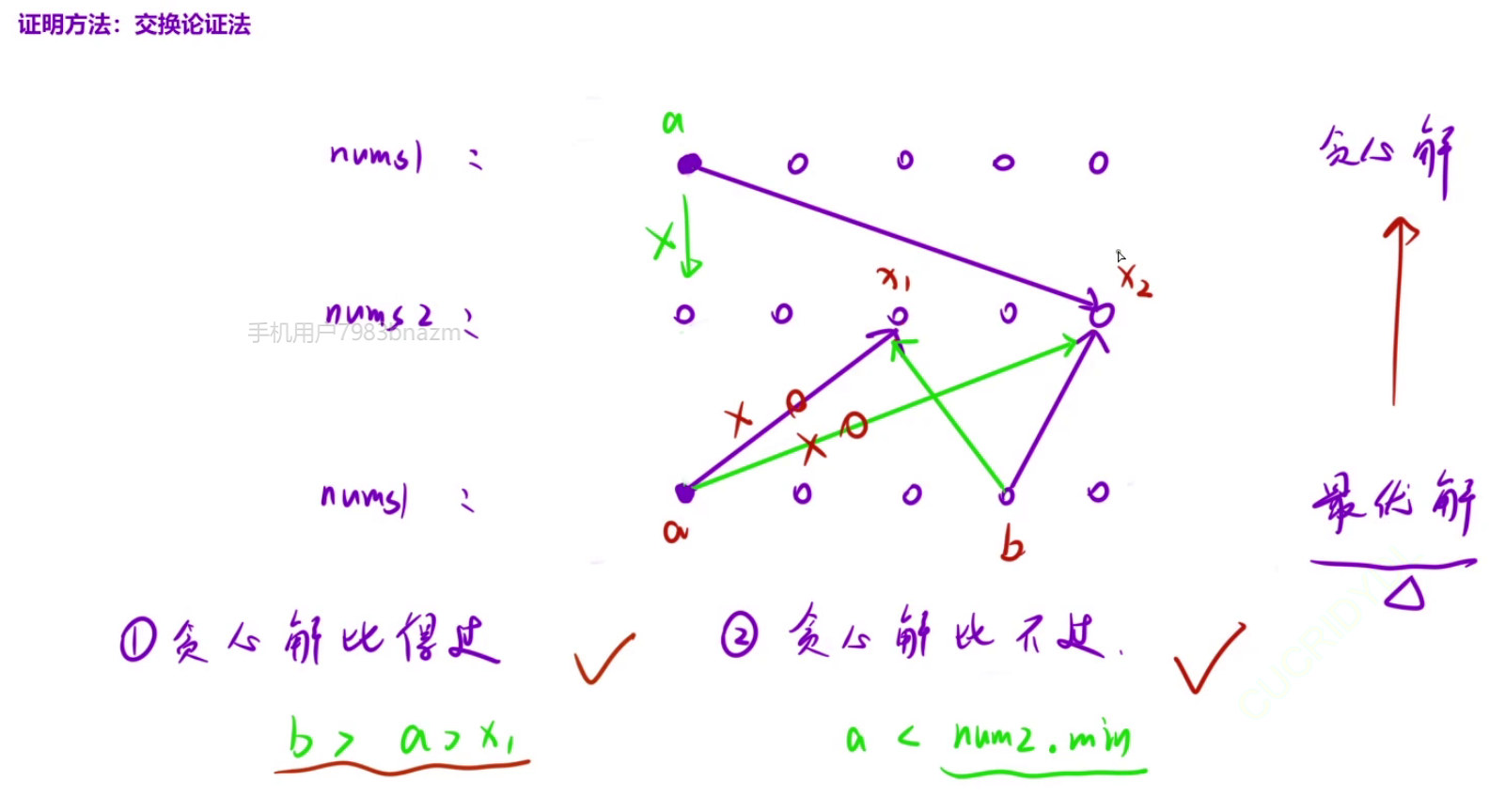
证明:
nums1[14,24,32,8]; nums2[ 13,25,32,11]
贪心解:ret[24,32,8,14] (贪心只有这一个,每回合出用最小的大于nums2的值、使用最小值去抵消nums最大值)
最优解(能使优势最大化的所有解法):ret=[14(13),32(25),8(32),24(11)] 可见14与24是可以交换的。 即最优解可以在不失最最有性的情况下转化成贪心解
13、最长回文串

class Solution {
public int longestPalindrome(String s) {
// 出现以此的字符只能去一个
// 出现过偶数次的字符可以去偶数个
int center = 0;
int[] hash = new int[52];
for(int i=0;i<s.length();i++){
char ch = s.charAt(i);
if('a'<=ch && ch<='z') hash[ch-'a']++;
if('A'<=ch && ch<='Z') hash[ch-'A'+26]++;
}
int sum = 0;
int count = 0;
for(int i=0;i<52;i++){
sum+=hash[i];
if(hash[i]%2==1){
count++;
}
}
if(count!=0) return sum - count +1;
else return sum;
}
}
// s只包含大小写字母,不含其他特殊字符
class Solution {
public int longestPalindrome(String s) {
// 1. 计数 - ⽤数组模拟哈希表
int[] hash = new int[127];
for (int i = 0; i < s.length(); i++) {
hash[s.charAt(i)]++;
}
// 2. 统计结果
int ret = 0;
for (int x : hash) {
ret += x / 2 * 2;
}
return ret < s.length() ? ret + 1 : ret;
}
}
// 吴老师代码,好精简
(若字母是偶数个,这偶数个字母都可以加入到回文串中;若字母只有1个,那么最多只能取一个放在回文串的中间。)->之所以这样搞,可以说是贪心,也可以说是找规律,和摆动序列一样。但无论是贪心还是找规律都要证明期正确性,虽然有时候显而易见,不用证明。
**连续的:**子数组、子字符串
**非连续的:**子序列、子串
14、增减字符串匹配

class Solution {
public int[] diStringMatch(String s) {
// 0,1,2,3,4
// 两个DD 就取最大的两个值,需要用的时候,随便用
int left = 0, right = s.length();
int[] ret = new int[right + 1];
int i = 0;
while (left < right) {
char ch = s.charAt(i);
if (ch == 'I')
ret[i++] = left++;
if (ch == 'D')
ret[i++] = right--;
}
ret[i] = left;
return ret;
}
}
很明显这个题目不止一个解,
贪心策略:
若i位置应满足num[i]<num[i+1]时,就将最小值放入nums[i];
若i位置应满足num[i]>num[i+1]时,就将最大值放入nums[i];
贪婪体现在我可以有多种选择时,选择了最值。因为对于有序数组找最值比较。
15、分发饼干

class Solution {
public int findContentChildren(int[] g, int[] s) {
int m = g.length;
int n = s.length;
Arrays.sort(g);
Arrays.sort(s);
int ret = 0;
int i=0,j=0;
while(i<m&&j<n){
if(g[i]<=s[j]){
ret++;
i++;
j++;
}else{
j++;
}
}
return ret;
}
}
class Solution {
public int findContentChildren(int[] g, int[] s) {
int m = g.length, n = s.length;
Arrays.sort(g);
Arrays.sort(s);
int ret = 0;
for (int i = 0, j = 0; i < m && j < n; j++) {
if (g[i] <= s[j]) {
ret++;
i++;
}
}
return ret;
}
}
**贪心策略:**也是田忌赛马,先去满足胃口小的孩子,每次都用比孩子的胃口大一点的饼干
也是对最值的贪心
16、最优除法★★★★


如果nums[i]不大于2,那么本题就不会有下面这个规律,不会这么简单。
这个题目更像找规律了,可以找同用解法看看

class Solution {
public String optimalDivision(int[] nums) {
int n = nums.length;
if(n==1) return nums[0]+"";
if(n==2) return nums[0]+"/"+nums[1];
StringBuffer str = new StringBuffer();
for(int i=0;i<n;i++){
if(i==0){
str.append(nums[i]+"/(");
}else if(i==n-1){
str.append(nums[i]);
}else{
str.append(nums[i]+"/");
}
}
str.append(")");
return str.toString();
}
}
17、跳跃游戏★★★★

class Solution {
public int jump(int[] nums) {
int ret = 0;
int n = nums.length;
int[] setp = new int[n];
setp[n-1]=0;
for(int i=n-2;i>=0;i--){
int min = Integer.MAX_VALUE;
for(int j=1;j<=nums[i]&&i+j<n;j++){
min = Math.min(min,setp[i+j]);
}
setp[i] = min==Integer.MAX_VALUE?min:min+1;
}
return setp[0];
}
}
// 动态规划,时间复杂度O(N^2)
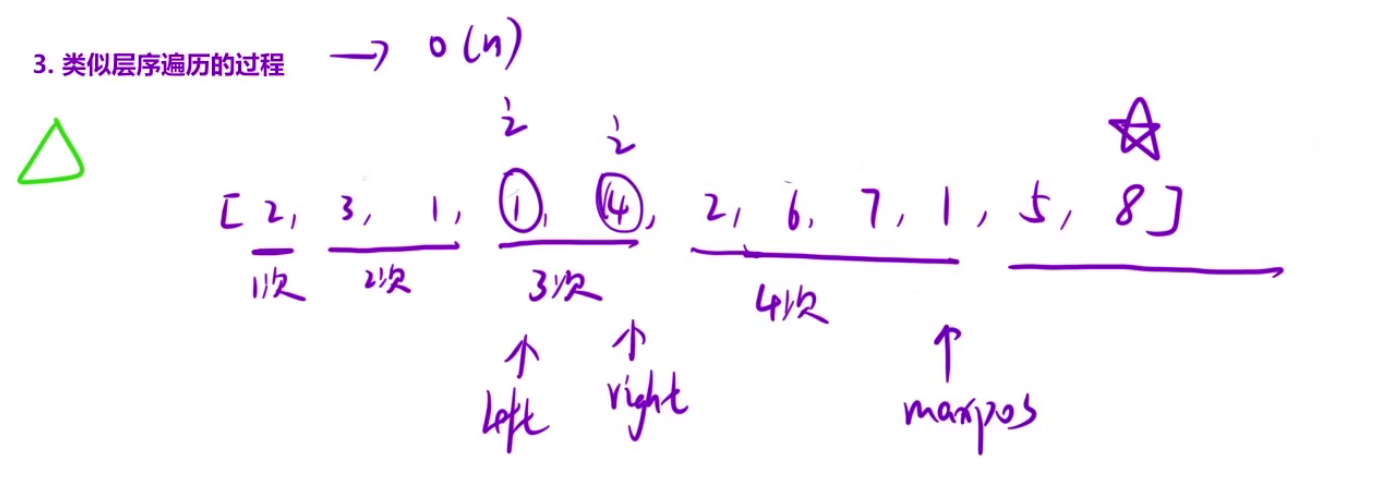
class Solution {
public int jump(int[] nums) {
// 类似于层序遍历
int left = 0, right = 0, ret = 0, maxPos = 0, n = nums.length;
while (left <= right) // 以防跳不到 n - 1 的位置
{
if (maxPos >= n - 1) // 判断是否已经能跳到最后⼀个位置
{
return ret;
}
for (int i = left; i <= right; i++) {
// 更新下⼀层的最右端点
maxPos = Math.max(maxPos, nums[i] + i);
}
left = right + 1;
right = maxPos;
ret++;
}
return -1;
}
}
// 也是正向查找,思想是一致的,官方写的更优雅
class Solution {
public int jump(int[] nums) {
int length = nums.length;
int end = 0;
int maxPosition = 0;
int steps = 0;
for (int i = 0; i < length - 1; i++) {
maxPosition = Math.max(maxPosition, i + nums[i]);
if (i == end) {
end = maxPosition;
steps++;
}
}
return steps;
}
}
作者:力扣官方题解
链接:https://leetcode.cn/problems/jump-game-ii/solutions/230241/tiao-yue-you-xi-ii-by-leetcode-solution/
来源:力扣(LeetCode)
著作权归作者所有。商业转载请联系作者获得授权,非商业转载请注明出处。

反向查找,但也是类似层序的思想
class Solution {
public int jump(int[] nums) {
int position = nums.length - 1;
int steps = 0;
while (position > 0) {
for (int i = 0; i < position; i++) {
if (i + nums[i] >= position) {
position = i;
steps++;
break;
}
}
}
return steps;
}
}
// 存在重复遍历
作者:力扣官方题解
链接:https://leetcode.cn/problems/jump-game-ii/solutions/230241/tiao-yue-you-xi-ii-by-leetcode-solution/
来源:力扣(LeetCode)
著作权归作者所有。商业转载请联系作者获得授权,非商业转载请注明出处。

恍惚之间分不清贪心策略和找规律之间的区别
18、跳跃游戏

class Solution {
public boolean canJump(int[] nums) {
int left = 0, right = 0, ret = 0, maxPos = 0, n = nums.length;
while (left <= right) // 以防跳不到 n - 1 的位置
{
if (maxPos >= n - 1) // 判断是否已经能跳到最后⼀个位置
{
return true;
}
for (int i = left; i <= right; i++) {
// 更新下⼀层的最右端点
maxPos = Math.max(maxPos, nums[i] + i);
}
left = right + 1;
right = maxPos;
ret++;
}
return false;
}
}
跳跃游戏<跳跃游戏II
19、加油站

class Solution {
public int canCompleteCircuit(int[] gas, int[] cost) {
// 环绕一周
int c = 0;
int index = 0;
int ret = index;
int n = gas.length;
while(ret<=index){
// 到地方加油
c+=gas[index%n];
c-=cost[index%n];
// 判断能否驶入到下一站点
if(c<0){
// 不能则说明从index之前的任何一个站点出发都不可能环游一周
// 从index+1位置重新开始判断
index++;
ret = index%n;
c=0;
// 说明这个位置被开启了第二次判断
if(index>ret) return -1;
}else{
if(ret == index%n && index>ret) return ret;
else index++;
}
}
return 0;
}
}
class Solution {
public int canCompleteCircuit(int[] gas, int[] cost) {
int n = gas.length;
for (int i = 0; i < n; i++) // 依次枚举所有的起点
{
int rest = 0; // 统计净收益
int step = 0;
for (; step < n; step++) // 枚举向后⾛的步数
{
int index = (i + step) % n; // ⾛ step 步之后的下标
rest = rest + gas[index] - cost[index];
if (rest < 0) {
break;
}
}
if (rest >= 0) {
return i;
}
i = i + step; // 优化
}
return -1;
}
}
**暴力解法:**遍历整个数组,从每一个位置开始模拟,看看从该位置是否可以环绕一周,整体的时间复杂度为O(N^2)
优化:对于gas = [2,3,4], cost = [3,4,3],找个例子模拟一下,不难看出从i加油出发位置开始开车到j加油后位置发现无法环游一周,就意味着从i~j加油站开始出发都都不可能环游一周,也就没有必要重新从i+1位置继续模拟了,而是从j+1位置开始模拟,看看能不能还有一周,若可以则返回该位置下标,若遍历完数组找不到可以遍历一周的起点则返回-1;
和第七题最长连续递增序列一样,指针没有没有必要回退,解题思路很好模拟,就是编码的细节问题比较难。
20、单调递增的数字

class Solution {
public int monotoneIncreasingDigits(int n) {
List<Integer> arr = new ArrayList<>();
while(n>0){
arr.add(n%10);
n/=10;
}
int m = arr.size();
for(int i=0;i<m-1;i++){
int cur = arr.get(i);
int pre = arr.get(i+1);
if(cur < pre){
int j=i;
while(j>=0 && arr.get(j)!=9 ) arr.set(j--,9);
arr.set(i+1,pre-1);
}
}
int num = 0;
for(int i=m-1;i>=0;i--){
num=num*10+arr.get(i);
}
return num;
}
}
// 从个位开始遍历,遇见高位数字pre大于低位数字cur时就将高位更新为pre-1,低于该为的全部更新为9
class Solution {
public int monotoneIncreasingDigits(int n) {
// 把数字转化成字符串
char[] s = Integer.toString(n).toCharArray();
int i = 0, m = s.length;
// 找第⼀个递减的位置
while (i + 1 < m && s[i] <= s[i + 1])
i++;
if (i == m - 1)
return n; // 特判⼀下特殊情况
// 回退
// 回退可以提前使用一个变量进行标记
while (i - 1 >= 0 && s[i] == s[i - 1])
i--;
s[i]--;
for (int j = i + 1; j < m; j++)
s[j] = '9';
return Integer.parseInt(new String(s));
}
}
// int n = 12345550
// int[] nums = [1,2,3,4,5,5,5,0]
从最高位向低位遍历i<j,若nums[i]<nums[j],则遍历下一位,若nums[i]>nums[j],第一个等于nums[i]的哪一位数值减1,该位置之后的数字都置为9
示例:
num=“123455555555554321”
遍历num字符串,一路遍历一路严格递增,直到遇见下降向在最后一个5借位,此时就打破了刚才一路非严格递增的规律,所以应该将第一个5将为4,最后一个5以及后面的数字都要改成9。
class Solution {
public int monotoneIncreasingDigits(int n) {
// 把数字转化成字符串
char[] s = Integer.toString(n).toCharArray();
int i = 0, m = s.length;
int start = 0;
// 找第⼀个递减的位置
while (i + 1 < m ){
if(s[i] == s[i + 1]){
i++;
}else if(s[i] < s[i + 1]){
i++;
start = i;
}else{
break;
}
}
if (i == m - 1)
return n; // 特判⼀下特殊情况
s[start]--;
for (int j = start+1; j < m; j++)
s[j] = '9';
return Integer.parseInt(new String(s));
}
}
恍惚之间分不清贪心策略和找规律
21、坏了的计算器★★★★★★★

class Solution {
public int brokenCalc(int startValue, int target) {
if(target<startValue) return startValue-target;
int setp = 0;
while(target>startValue){
if(target%2==0) target/=2;
else target+=1;
setp++;
}
return setp + startValue -target;
}
}
// 为什么这么写时正确的?
艹!想不明白这个算法的为什么是正确的!
22、合并区间

public class Solution {
public int[][] merge(int[][] intervals) {
// 首先对区间按照起始时间进行排序
Arrays.sort(intervals, (a, b) -> a[0] - b[0]);
List<int[]> merged = new ArrayList<>();
// 遍历排序后的区间
for (int[] interval : intervals) {
// 如果合并后的区间列表为空, 或者当前区间的起始时间大于合并后区间列表中最后一个区间的结束时间,
// 则直接将当前区间加入合并后的区间列表
if (merged.isEmpty() || interval[0] > merged.get(merged.size() - 1)[1]) {
merged.add(interval);
}
// 否则,将当前区间与合并后区间列表中最后一个区间进行合并
else {
merged.get(merged.size() - 1)[1] = Math.max(merged.get(merged.size() - 1)[1], interval[1]);
}
}
// 将合并后的区间列表转换为数组并返回
return merged.toArray(new int[merged.size()][]);
}
}
23、无重叠区间

class Solution {
public int eraseOverlapIntervals(int[][] intervals) {
// 1、排序
// 2、如果两个区间有交集,删除左端点大的区间,若左端点一样大,则删除区间长的那个
Arrays.sort(intervals, (a, b) -> a[0] - b[0]);
int ret = 0;
List<int[]> merged = new ArrayList<>();
for (int[] interval : intervals) {
// 新区间不与最后一个区间冲突,那么就直接add
if (merged.isEmpty() || interval[0] >= merged.get(merged.size() - 1)[1]) {
merged.add(interval);
}else {
// 如果新区间与最后一个区间冲突,那么一定不与倒数第二个区间冲突,
// 所以为了更大可能防止于后续的区间冲突,就选择右端点更小的区间进行保留。
if(interval[1] < merged.get(merged.size() - 1)[1]){
merged.set(merged.size()-1,interval);
}
ret++;
}
}
return ret;
}
}
贪心策略:若新区间不与最后一个区间冲突,那么就直接add。 如果新区间与最后一个区间冲突,那么一定不与倒数第二个区间冲突,所以为了更大可能防止于后续的区间冲突,就选择右端点更小的区间进行保留。
class Solution {
public int eraseOverlapIntervals(int[][] intervals) {
// 1、排序
// 2、如果两个区间有交集,删除右端点大的区间,以尽可能地避免后续区间发生冲突
Arrays.sort(intervals, (a, b) -> a[0] - b[0]);
int ret = 0;
int right = intervals[0][0];
for (int i=0;i<intervals.length;i++) {
int[] interval = intervals[i];
if (interval[0] >= right) {
right = interval[1];
}else {
if(interval[1] < right){
right = interval[1];
}
ret++;
}
}
return ret;
}
}
不需要存储一路合并的区间,使用两个变量描述最后一个区间即可!
24、用最少量的箭引爆气球

public class Solution {
public int findMinArrowShots(int[][] points) {
// 根据右端点进行排序
Arrays.sort(points, (a, b) -> a[0] > b[0] ? 1 : -1);
int num = 0;
int left = points[0][0];
int right = points[0][1];
for (int i = 0; i < points.length; i++) {
// 贪心策略:如果有重叠,缩小射箭区间,,为了可以同时引爆多个气球
// 每一只箭都射击了尽可能多的气球
int a = points[i][0], b = points[i][1];
if (a <= right) {
left = a;
if (b < right)
right = b;
} else {
num++;
left = a;
right = b;
}
}
return num + 1;
}
}
贪心策略:如果有重叠,缩小射箭区间,为了可以同时引爆多个气球,每一只箭都射击了尽可能多的气球。即使不对数组进行排序,气球也是重叠的,排序是为了只需要从左向右一直遍历就可以找打所有重叠的气球。不然每次都要遍历整个数组了。
25、整数替换

class Solution {
Map<Long,Integer> hash;
public int integerReplacement(int n) {
hash = new HashMap<>();
return integerReplacement2(n*1L);
}
public int integerReplacement2(long n) {
if(hash.containsKey(n)) return hash.get(n);
if(n<=1) return 0;
if(n%2==1){
int a = integerReplacement2(n-1);
int b = integerReplacement2(n+1);// n+1可能爆int
int ret = Math.min(a,b)+1;
hash.put(n,ret);
return ret;
}else{
int c = integerReplacement2(n/2)+1;
hash.put(n,c);
return c;
}
}
}
class Solution {
Map<Long,Integer> hash;
public int integerReplacement(int n) {
hash = new HashMap<>();
return integerReplacement2(n*1L);
}
public int integerReplacement2(long n) {
if(n<=1) return 0;
if(n%2==1){
int a = hash.getOrDefault(n,integerReplacement2(n-1));
int b = hash.getOrDefault(n,integerReplacement2(n+1));// n+1可能爆int
int ret = Math.min(a,b)+1;
hash.put(n,ret);
return ret;
}else{
int c = hash.getOrDefault(n,integerReplacement2(n/2)+1);
hash.put(n,c);
return c;
}
}
}
// 递归层数太多了,可以使用记忆化搜索
虽然时间复杂度是O(logN),但是我的频繁使用了getOrDefault()所以整体比吴老师地代码慢了很多


class Solution {
// 贪心算法:
public int integerReplacement(int n) {
int step = 0;
while (n > 1) {
if (n % 2 == 0) {
n /= 2;
step++;
} else {
if (n == 3) {
return step + 2;
} else {
if (n % 4 == 1) {
n /= 2;
step += 2;
} else {
n = n / 2 + 1; // (n+1)/2 可能会溢出
step += 2;
}
}
}
}
return step;
}
}
这题目是真的难,不过动态规划和递归深搜也能解决
26、俄罗斯套娃信封问题

class Solution {
public int maxEnvelopes(int[][] e) {
// 解法⼀:动态规划
Arrays.sort(e, (v1, v2) -> {
return v1[0] - v2[0];
});
int n = e.length;
int[] dp = new int[n];
int ret = 1;
for (int i = 0; i < n; i++) {
dp[i] = 1; // 初始化
for (int j = 0; j < i; j++) {
if (e[i][0] > e[j][0] && e[i][1] > e[j][1]) {
dp[i] = Math.max(dp[i], dp[j] + 1);
}
}
ret = Math.max(ret, dp[i]);
}
return ret;
}
}
// 动态规划
// 时间复杂度O(N^2)。dp[i]代表以第i封信为结尾的最高层数
// 这个解法和最后一种只对左端点排序的解法很像
class Solution {
public int maxEnvelopes(int[][] envelopes) {
Arrays.sort(envelopes, (a, b) -> {
if (a[0] != b[0]) {
return a[0] < b[0] ? -1 : 1;
}
return a[1] > b[1] ? -1 : 1;
});
int m = envelopes.length;
List<Integer> ret = new ArrayList<>();
ret.add(envelopes[0][1]);
for (int i = 0; i < m; i++) {
int b = envelopes[i][1];
if (b > ret.get(ret.size() - 1)) {
ret.add(b);
} else {
int left = 0, right = ret.size() - 1;
// 二分查找第一个大于等于b的数字
while (left < right) {
int mid = left + (right - left) / 2;
if (ret.get(mid) < b) {
left = mid+1;
} else {
right = mid;
}
}
ret.set(left, b);
}
}
return ret.size();
}
}
// 重排序+贪心+二分
首先数组要根据左端点进行排序,这样一来某一侧信封一定装不下它左侧的信封,从第一个信封开始寻找更大的信封只需向右遍历数组即可,对于下面这个特例,原问题就转化为了最长递增子序列问题:这这个特例的特点就是左端点不重复,也就意味着继续套娃信封的时候仅需考虑右端点是大于当前信封的右端点,则最大套娃信封的数量就是排序后右端点构成的一维数组的最长递增子序列问题。
但是信封中左端点存在重复,并不是唯一的。对于下面这些信封,最大套娃数是1。用最长递增子序列计算的结果则是4。左端点虽然递增,但是右端一样大说明不能套娃。
但是如果将右端点进行从大到小排序,那么无论从左端点的角度看还是右端点的角度看都不能套娃,可以使用最长递增子序列来解决这道题:
经验嘛,如果对左端点排序有助于解题,那么右端点也排序也可能有帮助。
其实只对左端点排序,也肯一使用与"最长递增子序列"类似的策略解题,如下图
解决最长递增子序列使用的链表,每个位置只会存储1个元素,我的这个需要存储多个元素。
cur=[2,100]:ret.get(0).add(cur);
cur=[3,200]:因为ret.get(0)中的所有信封都可以装入[3,100],说明可以扩展新的层数
cur=[4,300]:因为ret.get(0)和ret.get(1)的信封都小于[4,300],说明可以继续扩展到下一层
cur=[5,500]:同样是大于目前的所有信封可以继续扩展到下一层
cur=[5,400]:发现前两层[5,400]都可以套住,套不住第三层的[5,250],所以只能留在第三层而不能放在第四层
cur=[6,370]:同理[6,370]只能留在第四层
cur=[6,360]:同理[6,360]只能留在第四层 (漏画了)
cur=[6,380]:同理[6,380]可以扩展到第五层。
这个方式的时间复杂度是O(N^2),虽然不如双端重排序优秀,但这是我自己想出来的。
这个解法和动态规划很像
27、可被三整除地最大和 ★★★★(正难则反)

下面代码的注释很重要
class Solution {
public int maxSumDivThree(int[] nums) {
// 先找出所有三的倍数
// 遍历
// 如果a%3+b%3==3,那么(a+b)%3==0
// 如果a%3==b%3==c%3==1,那么(a+b+c)%3==0
// [4,4,4]也可以。艹,这个策略不太行
// 先把所有数累加
// 若sum%3==0,则return sum;
// 若sum%3==1,则删除一个最小和x,s%3==1
// 若sum%3==2,则删除一个最小和x,s%3==2
//对所有数分类
// 1 4 7
// 3 6 9
// 2 5 8
// 若sum%3==1,则删除一个模3等于一的数字,或者两模3等于2的数字
// 若sum%3==2,则删除一个模3等于二的数字,或者两模3等于1的数字
Arrays.sort(nums);
List<Integer> yu1 = new ArrayList<>();
List<Integer> yu2 = new ArrayList<>();
int sum=0;
for(int i=0;i<nums.length;i++){
sum+=nums[i];
if(nums[i]%3==1) yu1.add(nums[i]);
if(nums[i]%3==2) yu2.add(nums[i]);
}
if(sum%3==0){
return sum;
}else if(sum%3==1){
int min = sum;
if(yu1.size()>=1){
min = yu1.get(0);
}
if(yu2.size()>=2){
min = Math.min(min,yu2.get(0)+yu2.get(1));
}
return sum-min;
}else{
int min = sum;
if(yu1.size()>=2){
min = yu1.get(0)+yu1.get(1);
}
if(yu2.size()>=1){
min = Math.min(min,yu2.get(0));
}
return sum-min;
}
}
}
class Solution {
public int maxSumDivThree(int[] nums) {
int INF = 0x3f3f3f3f;
int sum = 0, x1 = INF, x2 = INF, y1 = INF, y2 = INF;
// 使用四个变量存储最小值和次小值
for (int x : nums) {
sum += x;
if (x % 3 == 1) {
if (x < x1) {
x2 = x1;
x1 = x;
} else if (x < x2) {
x2 = x;
}
} else if (x % 3 == 2) {
if (x < y1) {
y2 = y1;
y1 = x;
} else if (x < y2) {
y2 = x;
}
}
}
// 分类讨论
if (sum % 3 == 0)
return sum;
else if (sum % 3 == 1)
return Math.max(sum - x1, sum - y1 - y2);
else
return Math.max(sum - y1, sum - x1 - x2);
}
}
// 钻了数据范围的漏洞,因为x1,x2,y1,y2是有可能还能与INF,
// 分类讨论时存在INF的哪一项结果为负数,不可能被return
// 如果sum % 3 == 0,那有变量不等于INF,所以一定会返回正数
// 无论是几的倍数能都解决
28、距离相等的条形码

// 把这些分类存储起来,然后构造返回值
// 贪心策略:尽量某两个数交替,而不是三个数进行交替
// 出现次数最多的数字x
// 其他数
// 先在偶数位置放置x
// 因为题目保证有解,所以x的数量最多是数组的一半
// 所以当x填入偶数位置以后,其他数按照顺序填入是不可能出现相同数字相邻的情况。
class Solution {
public int[] rearrangeBarcodes(int[] b) {
int n = b.length;
int[] ret = new int[n];
int index = 0;
// 先处理出现次数最多的那个数
for (int i = 0; i < maxCount; i++) {
ret[index] = maxVal;
index += 2;
}
hash.remove(maxVal);
for (int x : hash.keySet()) {
for (int i = 0; i < hash.get(x); i++) {
if (index >= n)
index = 1;
ret[index] = x;
index += 2;
}
}
return ret;
}
}
没想出来要先处理出现次数最多的数字
力扣好像有道题目是一个数组中有一个数出现了一半以上,问这个数是那个数。
29、重构的字符串

class Solution {
public String reorganizeString(String s) {
// 只要出现次数最多的的那个元素不超过一半就可以重新排序
// 统计每个数出现了多少次
int n = s.length();
int[] hash = new int[26];
char maxChar = ' ';int maxCount = 0;
for (int i=0;i<n;i++) {
char ch = s.charAt(i);
hash[ch-'a']++;
if (maxCount < hash[ch-'a']) {
maxChar = ch;
maxCount = hash[ch-'a'];
}
}
if(2*maxCount>n+1) return "";
char[] str = new char[n];
// 先填充出现次数最多的字符
int index = 0;
for(int i=0;i<maxCount;i++){
str[index]=maxChar;
index+=2;
}
// 移除该字符
hash[maxChar-'a']=0;
// 填充其他字符
for(int i=0;i<26;i++){
for(int j=0;j<hash[i];j++){
if(index>=n) index=1;
str[index]=(char)('a'+i);
index+=2;
}
}
return new String(str);
}
}
最重要的一个思路就是先处理出现次数最大的元素。