一,归并排序
归并排序(Merge sort)是建立在归并操作上的一种有效的排序算法。该算法分治法(Divide and Conquer)的一个非常典型的应用。
作为一种典型的分而治之思想的算法应用,归并排序的实现由两种方法:
1.自上而下的递归(所有递归的方法都可以用迭代重写)
2.自下而上的迭代
1.基本思想
归并排序(MERGE-SORT)是建立在归并操作上的一种有效的排序算法。将已有序的子序列合并,得到完全有序的序列;即先使每个子序列有序,再使子序列段间有序。若将两个有序表合并成一个有序表,称为二路归并。
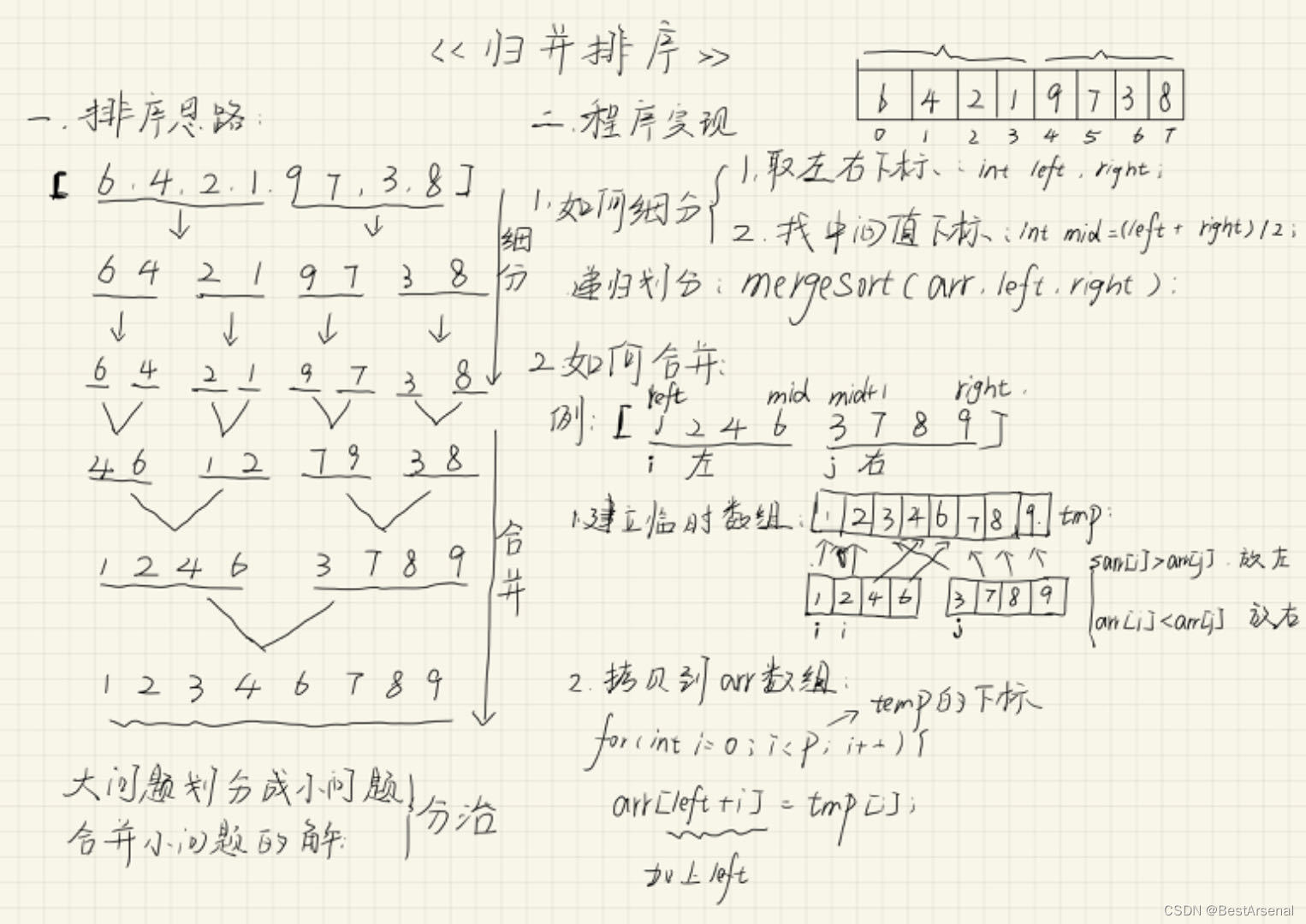
简而言之,先通过递归的思想将数组分成一个一个的不可再分的子序列,接下来再对其中两个子序列按照升序或者降序合并,重复直到合并所有子序列合并完成。(子问题其实就是两个有序数组的合并)。
2.程序实现
#include<iostream>
using namespace std;
#define eleType int
//合并两个有序子序列
/*
参数含义: arr数组, left:序列的左边起始点 mid:中间下标 right:右边结束点
通过left mid right 将arr分成左右两个区域
*/
void merge(eleType *arr,int left,int mid,int right){
int i = left, j = mid + 1; // i为左边区域的指针 j 为右边区域的指针
eleType *temp = new eleType[right + 1]; //临时数组,用来临时存放排序后的数字
int index = 0; //临时数组的下标
while(i <= mid && j <= right){ //当左右区域都有未比完的数字
temp[index++] = arr[i] < arr[j] ? arr[i++] : arr[j++]; //选择较小的存入temp数组
}
while(i <= mid){ //当仅剩左边区域
temp[index++] = arr[i++]; // 按顺序存入temp
}
while(j <= right){ //当仅剩右边区域
temp[index++] = arr[j++]; //按顺序存入temp
}
for(int i = 0; i < index; i++){ //将temp重新放回arr
arr[left + i] = temp[i];
}
delete [] temp; //删除临时temp数组
}
//归并排序
/*
参数含义: left:最左边下标 right : 最右边的下标
通过left 和right 计算出中间数的下标
*/
void mergesort(eleType *arr,int left,int right){
if(left < right){ //递归条件
int mid = left + (right - left) / 2; //计算中间下标
mergesort(arr,left,mid); //递归划分左边区域
mergesort(arr,mid + 1, right);//递归划分右区域
merge(arr,left,mid,right); //执行合并
}
}
3.优缺点:
优点
稳定性: 稳定的排序算法,即相同元素的相对顺序在排序前后保持不变。
最佳、平均和最坏时间复杂度:归并排序在所有情况下(包括输入数组已排序或逆序)的时间复杂度都是O(n log n),n是数组的大小。它在处理大数据集时非常高效。
空间复杂度:虽然归并排序需要额外的空间来存储临时子数组,但它的空间复杂度是O(n),在实际应用中通常是可以接受的。
缺点
空间复杂度:虽然O(n)的空间复杂度可以接受的,但对于内存受限的环境或需要就地排序的场合,归并排序不是最佳选择。
数据移动次数:归并排序在合并过程中可能需要大量的数据移动操作,这可能导致在某些情况下效率较低。
不适合小数据集:对于非常小的数据集,归并排序的额外空间开销和递归调用相对于其他简单排序算法效率较低。但是在大数据集上,归并排序的O(n log n)时间复杂度远优于这些简单排序算法。
递归深度:归并排序是递归算法,对于非常大的数据集,递归深度可能会很大,可能导致栈溢出。
二,快速排序
1.基本思想
通过一次排序将待排序的数据分割成独立的两部分,其中一部分的所有数据都比另一部分的所有数据都要小,然后再按此方法对这两部分数据分别进行快速排序,整个排序过程可以递归进行,以此达到整个数据变成有序序列。

2.实现步骤
- 1.选择一个基准元素(pivot):通常选择待排序序列的第一个或最后一个元素作为基准。
- 2.分割过程:将序列中小于基准的元素放在基准的左边,大于基准的元素放在基准的右边。这个过程称为分区(partition)操作,分区结束后基准元素所处的位置就是其在已排序序列中的正确位置。
- 3.递归排序:分别对基准左右两边的子序列进行快速排序。
3.代码实现
#include<iostream>
using namespace std;
#define eleType int
/*
划分 将比基准数大的放右边,比基准数小的放左边
参数含义: arr数组,left:最左边的下标 right: 最右边的下标
*/
int getKeyPositon(eleType *arr,int left,int right){
int key = arr[left]; //将第一个数作为基准数
while(left < right){
while(arr[right] >= key && left < right){ //右边先移动,找比基准数小的
right--;
}
arr[left] = arr[right]; //找到之后赋值给左边left的位置
while(arr[left] <= key && left < right){ //之后左边移动,找比基准数大的
left++;
}
arr[right] = arr[left];//找到之后赋值给右边right的位置
}
arr[left] = key; //左右指针相遇之后,将基准数放回相遇的位置
return left; //返回基准数的位置
}
/*
排序过程,不停的基准数放到正确位置
参数含义: arr数组,left:最左边的下标 right: 最右边的下标
*/
void quickSort(eleType *arr,int left,int right){
if(left < right){ //递归条件
int position = getKeyPositon(arr,left,right); //基准数归位之后,数组被分成左右两部分
quickSort(arr,left,position - 1); //对左边部分排序
quickSort(arr,position + 1,right); //对右边部分排序
}
}
优缺点
优点:
速度快:在平均情况下,快速排序的时间复杂度为O(n log n),比许多排序算法都要快。
原地排序:只需要一个很小的栈空间来保存递归的调用,不需要额外的存储空间。
缺点:
最坏情况:在最坏情况下(输入数据已经有序或接近有序),快速排序的时间复杂度会退化到O(n^2)。
空间复杂度:虽然快速排序是原地排序,但在递归调用时可能会占用较大的栈空间。对于非常大的数据集,会导致栈溢出。
对基准元素的选择敏感:基准元素的选择会影响到排序的性能。如果每次选择的基准元素都是序列中最小或最大的元素,排序的效率就会降低。