本文字数：15474；估计阅读时间：39 分钟

审校：庄晓东（魏庄）

本文在公众号【ClickHouseInc】首发

Meetup活动

ClickHouse 上海首届 Meetup 讲师招募中，欢迎讲师在文末扫码报名！

 介绍

最近，在帮助一位用户解决从 ClickHouse 中提取向量并计算质心的问题时，我们意识到同样的解决方案也可以用于实现 K-Means 聚类。他们希望在可能涉及数十亿数据点的情况下扩展此解决方案，同时确保能够严格管理内存。在本文中，我们尝试仅使用 SQL 实现 K-Means 聚类，并展示其在处理数十亿行数据时的扩展能力。 

在撰写本文时，我们注意到了 Boris Tyshkevich 的相关工作。虽然我们在本文中采用了不同的方法，但我们要感谢 Boris 的工作，并感谢他在我们之前就已经有了这个想法！

作为使用 ClickHouse SQL 实现 K-Means 的一部分，我们在不到 3 分钟内对纽约市的 1.7 亿次出租车行程进行了聚类。相比之下，相同资源下，使用 scikit-learn 进行的操作耗时超过 100 分钟，并且需要 90GB 的 RAM。在没有内存限制的情况下，并且 ClickHouse 自动分发计算，我们展示了 ClickHouse 能够加速机器学习工作负载，并缩短迭代时间。

本博客文章的所有代码都可以在这里的笔记本文件【https://github.com/ClickHouse/examples/blob/main/blog-examples/kmeans/kmeans.ipynb】中找到。

为什么要在 ClickHouse SQL 中使用 K-Means？

在 ClickHouse SQL 中使用 K-Means 的主要原因是，训练过程不受内存限制，这意味着可以通过增量计算质心（同时限制内存开销）来对 PB 数据集进行聚类。与此相反，如果使用基于 Python 的方法来在服务器之间分布此工作负载，则需要额外的框架和复杂性。

此外，我们可以轻松提高聚类中的并行度，以充分利用 ClickHouse 实例的全部资源。如果需要处理更大的数据集，只需扩展数据库服务 - 这在 ClickHouse Cloud 中是一项简单的操作。

将数据转换为 K-Means 的简单 SQL 查询每秒可以处理数十亿行数据。在 ClickHouse 中保存质心和点，我们可以仅通过 SQL 计算诸如模型误差之类的统计数据，并且可能将我们的聚类用于其他操作，例如用于向量搜索的产品量化。

K-Means 摘要

K-Means 是一种无监督机器学习算法，用于将数据集分成 K 个不同的、不重叠的子组（簇），其中每个数据点属于最近均值（簇的质心）的簇。该过程从随机初始化 K 个质心或基于某些启发式方法开始。这些质心作为簇的初始代表。然后，该算法通过两个主要步骤迭代直至收敛：分配和更新。

在分配步骤中，根据数据点与质心之间的欧几里德距离（或其他距离度量）将每个数据点分配给最近的簇。在更新步骤中，重新计算质心，作为分配给各自簇的所有点的平均值，可能会改变它们的位置。

该过程保证收敛，点到簇的分配最终会稳定下来，在迭代之间不会改变。需要事先指定簇的数量 K，并且这个值会对算法的有效性产生重大影响，最佳值取决于数据集和聚类的目标。欲知更多详细信息，我们推荐阅读这篇概述。

数据点与质心

我们的用户提出的关键问题是高效计算质心的能力。假设我们有一个交易表的简单数据模式，其中每行记录了特定客户的一笔银行交易。在 ClickHouse 中，向量被表示为数组类型。

CREATE TABLE transactions
(
  id UInt32,
  vector Array(Float32), 
  -- e.g.[0.6860357,-1.0086979,0.83166444,-1.0089169,0.22888935]
  customer UInt32,
  ...other columns omitted for brevity
)
ENGINE = MergeTree ORDER BY id

用户希望为每个客户找到质心，即与每个客户关联的所有交易向量的位置平均值。为了找到一组平均向量，我们可以使用 avgForEach[1][2] 函数。例如，考虑计算 3 个向量的平均值，每个向量有 4 个元素的示例：

WITH vectors AS
   (
       SELECT c1 AS vector
       FROM VALUES([1, 2, 3, 4], [5, 6, 7, 8], [9, 10, 11, 12])
   )
SELECT avgForEach(vector) AS centroid
FROM vectors

┌─centroid──┐
│ [5,6,7,8] │
└───────────┘

在我们原始的交易表中，计算每个客户的平均值就变得如下：

SELECT customer, avgForEach(vector) AS centroid FROM transactions GROUP BY customer

虽然这种方法简单，但存在一些限制。首先，对于非常大的数据集，当向量包含许多 Float32 点，且客户列具有许多唯一元素（高基数）时，此查询可能会占用大量内存。其次，对于 K-Means 更为关键的是，此方法要求我们在插入新行时重新运行查询，这是低效的。我们可以通过 Materialized Views 和 AggregatingMergeTree 引擎解决这些问题。

 使用 Materialized Views 增量计算质心

Materialized Views 允许我们将计算质心的成本转移到插入时间。在 ClickHouse 中，Materialized View 实际上是一个触发器，它在数据块插入到表中时运行一个查询。该查询的结果被插入到第二个“目标”表中。在我们的情况下，Materialized View 查询将计算我们的质心，并将结果插入到一个名为 centroids 的表中。

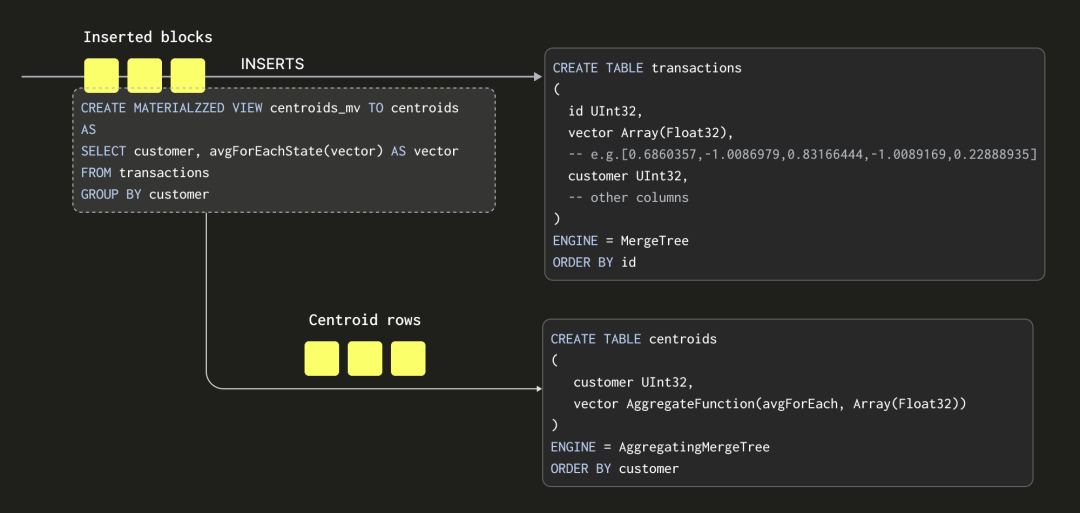
这里有一些重要的细节：

• 我们的查询，用于计算质心，必须以一种可以与后续结果集合并的格式生成结果集 - 因为每个插入的数据块都会产生一个结果集。我们不仅仅将平均值发送到我们的质心表（平均值的平均值将是不正确的），而是发送“平均状态”。平均状态表示包含每个向量位置的总和，以及一个计数。这是通过使用 avgForEachState 函数实现的 - 请注意我们刚刚在函数名后面添加了 State！需要 AggregatingMergeTree 表引擎来存储这些聚合状态。我们在下面进一步探讨这一点。

• 整个过程是增量的，质心表包含最终状态，即每个质心一行。读者会注意到，接收插入的表具有 Null 表引擎。这会导致插入的行被丢弃，节省了写入完整数据集的 IO 操作所需的时间。

• 我们的 Materialized View 的查询仅在数据块插入时执行。每个数据块中的行数可以根据插入方法而变化。如果在客户端组合块（例如，使用 Go 客户端）时，建议每个块至少包含 1000 行。如果服务器留给形成块（例如，通过 HTTP 插入），也可以指定大小。

• 如果使用 INSERT INTO SELECT，其中 ClickHouse 从另一个表或外部来源（例如 S3）读取行，则块大小可以通过之前博客中详细讨论的几个关键参数来控制。这些设置（以及插入线程的数量）可以显著影响所使用的内存量（更大的块 = 更多的内存）和摄取速度（更大的块 = 更快）。这些设置意味着可以通过性能来精细控制使用的内存量。

AggregatingMergeTree

我们的目标表 centroids 使用了 AggregatingMergeTree 引擎：

CREATE TABLE centroids
(
   customer UInt32,
   vector AggregateFunction(avgForEach, Array(Float32))
)
ENGINE = AggregatingMergeTree  ORDER BY customer

这里的向量列包含了上面 avgForEachState 函数生成的聚合状态。这些是必须合并以产生最终答案的中间质心。此列需要是适当类型的 AggregateFunction(avgForEach, Array(Float32))。

与所有 ClickHouse MergeTree 表一样，AggregatingMergeTree 将数据存储为必须透明合并以允许更高效查询的部分。当合并包含我们的聚合状态的部分时，必须这样做，以便只有与同一客户相关的状态被合并。这实际上是通过使用 ORDER BY 子句按客户列对表进行排序来实现的。在查询时，我们还必须确保中间状态被分组和合并。这可以通过确保我们按客户列进行 GROUP BY，并使用 avgForEach 函数的合并等效函数：avgForEachMerge 来实现。

SELECT customer, avgForEachMerge(vector) AS centroid
FROM centroids GROUP BY customer

所有聚合函数都有一个等价的状态函数，通过在它们的名称后面添加 State 来获得，该函数产生一个中间表示，可以存储，然后使用合并等效函数检索和合并。有关更多详细信息，我们推荐阅读这篇博客和 Mark 的视频。

与我们之前的 GROUP BY 相比，这个查询将会非常快。计算平均值的大部分工作已经移动到插入时间，只剩下一小部分行用于查询时合并。考虑以下两种方法的性能，使用 100m 个随机交易在一个 48GiB、12 vCPU 的云服务上。加载数据的步骤在这里。

对比从交易表计算我们的质心的性能：

SELECT customer, avgForEach(vector) AS centroid
FROM transactions GROUP BY customer
ORDER BY customer ASC
LIMIT 1 FORMAT Vertical

10 rows in set. Elapsed: 147.526 sec. Processed 100.00 million rows, 41.20 GB (677.85 thousand rows/s., 279.27 MB/s.)

Row 1:
──────
customer: 1
centroid: [0.49645231463677153,0.5042792240640065,...,0.5017436349466129]

1 row in set. Elapsed: 36.017 sec. Processed 100.00 million rows, 41.20 GB (2.78 million rows/s., 1.14 GB/s.)
Peak memory usage: 437.54 MiB.

与计算质心表相比，速度提高了超过 1700 倍：

SELECT customer, avgForEachMerge(vector) AS centroid
FROM centroids GROUP BY customer
ORDER BY customer ASC
LIMIT 1
FORMAT Vertical

Row 1:
──────
customer: 1
centroid: [0.49645231463677153,0.5042792240640065,...,0.5017436349466129]

1 row in set. Elapsed: 0.085 sec. Processed 10.00 thousand rows, 16.28 MB (117.15 thousand rows/s., 190.73 MB/s.)

 将所有内容整合在一起

利用我们逐步计算质心的能力，让我们专注于 K-Means 聚类。假设我们试图对一个名为 points 的表进行聚类，其中每行都有一个向量表示。在这里，我们将根据相似性进行聚类，而不仅仅像我们在交易中那样以客户为基础计算质心。

单次迭代

在算法的每次迭代后，我们需要能够存储当前的质心。现在，让我们假设我们已经确定了 K 的最优值。我们质心的目标表可能如下所示：

CREATE TABLE centroids
(
  k UInt32,
  iteration UInt32,
  centroid UInt32,
  vector AggregateFunction(avgForEach, Array(Float32))
)
ENGINE = AggregatingMergeTree 
ORDER BY (k, iteration, centroid)

k 列的值被设置为我们选择的 K 值。这里的 centroid 列表示质心编号本身，取值范围在 0 到 K-1 之间。我们不使用每次迭代算法的单独表，而是简单地包含一个 iteration 列，并确保我们的排序键是 (k, iteration, centroid)。ClickHouse 将确保只为每个唯一的 K、centroid 和 iteration 合并中间状态。这意味着我们的最终行数将很小，确保对这些质心进行快速查询。

我们用于计算质心的 Materialized View 应该很熟悉，只需进行小幅调整，还要对 k、centroid 和 iteration 进行 GROUP BY：

CREATE TABLE temp
(
   k UInt32,
   iteration UInt32,
   centroid UInt32,
   vector Array(Float32)
)
ENGINE = Null

CREATE MATERIALIZED VIEW centroids_mv TO centroids
AS SELECT k, iteration, centroid, avgForEachState(vector) AS vector
FROM temp GROUP BY k, centroid, iteration

请注意，我们的查询是在插入到临时表而不是数据源表 transactions 中的块上执行的，因为后者没有 iteration 或 centroid 列。这个临时表将接收我们的插入，并且再次使用 Null 表引擎来避免写入数据。有了这些基础，我们可以想象算法的单次迭代，假设 K = 5：

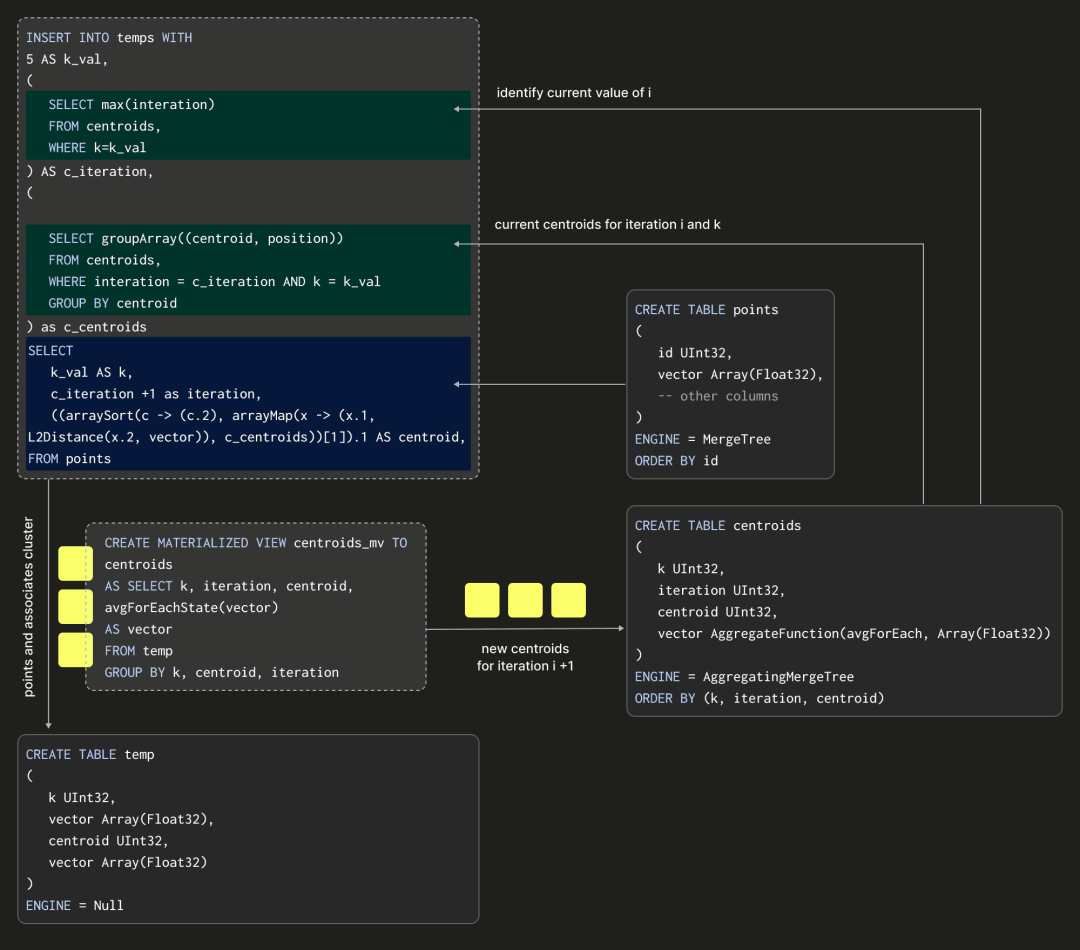
以上展示了我们如何通过在临时表中进行插入操作，并以 points 表作为源数据，来计算我们的质心。这样的插入实际上代表了算法的一次迭代。这里的 SELECT 查询至关重要，因为它需要指定交易向量及其当前的质心和迭代次数（以及固定的 K 值）。我们如何计算后两者呢？完整的 INSERT INTO SELECT 如下所示：

INSERT INTO temp 
WITH
  5 as k_val,
  -- (1) obtain the max value of iteration - will be the previous iteration
  (
      SELECT max(iteration)
      FROM centroids 
      -- As later we will reuse this table for all values of K
      WHERE k = k_val
  ) AS c_iteration,
  (
      -- (3) convert centroids into a array of tuples 
      -- i.e. [(0, [vector]), (1, [vector]), ... , (k-1, [vector])]
      SELECT groupArray((centroid, position))
      FROM
      (
         -- (2) compute the centroids from the previous iteration
          SELECT
              centroid,
              avgForEachMerge(vector) AS position
          FROM centroids
          WHERE iteration = c_iteration AND k = k_val
          GROUP BY centroid
      )
  ) AS c_centroids
SELECT
  k_val AS k,
  -- (4) increment the iteration
  c_iteration + 1 AS iteration,
  -- (5) find the closest centroid for this vector using Euclidean distance
  (arraySort(c -> (c.2), arrayMap(x -> (x.1, L2Distance(x.2, vector)), c_centroids))[1]).1 AS centroid,
  vector AS v
FROM points

首先，在 (1) 处，这个查询确定了上一次迭代的编号。然后在 (2) 处的 CTE 中使用该编号来确定此迭代（和选择的 K）产生的质心，使用之前展示的相同的 avgForEachMerge 查询。这些质心通过 groupArray 查询合并为包含 Tuple 数组的单行，以便与 points 进行匹配。在 SELECT 中，我们递增了迭代号码（4），并使用 arrayMap 和 arraySort 函数为每个点计算新的最近质心（使用欧几里得距离 L2Distance 函数）。

通过在这里基于上一次迭代的质心插入行到临时表，我们可以允许 Materialized View 计算新的质心（使用迭代值 +1）。

初始化质心

以上假设我们对迭代 1 有一些初始质心，用于计算成员资格。这需要我们初始化系统。我们可以通过简单地选择并插入 K 个随机点来完成此查询（k=5）：

INSERT INTO temp WITH 
  5 as k_val,
  vectors AS
  (
      SELECT vector
      FROM points
      -- select random points, use k to make pseudo-random
      ORDER BY cityHash64(concat(toString(id), toString(k_val))) ASC
      LIMIT k_val -- k
  )
SELECT
  k_val as k,
  1 AS iteration,
  rowNumberInAllBlocks() AS centroid,
  vector
FROM vectors

成功的聚类非常依赖于质心的初始放置；糟糕的分配会导致收敛缓慢或次优的聚类结果。我们稍后会详细讨论这个问题。

质心的分配和何时停止迭代

以上描述的是单次迭代（和初始化步骤）。在每次迭代后，我们需要根据一种经验性的度量来决定是否停止，这个度量可以衡量聚类是否已经收敛。最简单的方法是当点在迭代之间不再改变质心（从而改变聚类）时停止。

为了确定哪些点属于哪个质心，我们可以随时使用我们之前插入操作的 SELECT 查询。

为了计算上一次迭代中移动到不同聚类的点的数量，我们首先计算了前两次迭代的质心。使用这些质心，我们为每个迭代中的每个点确定了其所属的质心。如果两次迭代中对于同一个点的质心是相同的，我们返回 0，否则返回 1。这些值的总和提供了移动到不同聚类的点的数量。

WITH 5 as k_val,
(
      SELECT max(iteration)
      FROM centroids
) AS c_iteration,
(
  -- (1) current centroids
  SELECT groupArray((centroid, position))
  FROM
  (
      SELECT
          centroid,
          avgForEachMerge(vector) AS position
      FROM centroids
      WHERE iteration = c_iteration AND k = k_val
      GROUP BY centroid
  )
) AS c_centroids,
(
  -- (2) previous centroids
  SELECT groupArray((centroid, position))
  FROM
  (
      SELECT
          centroid,
          avgForEachMerge(vector) AS position
      FROM centroids
      WHERE iteration = (c_iteration-1) AND k = k_val
      GROUP BY centroid
  )
) AS c_p_centroids
-- (6) sum differences
SELECT sum(changed) FROM (
  SELECT id,
  -- (3) current centroid for point
  (arraySort(c -> (c.2), arrayMap(x -> (x.1, L2Distance(x.2, vector)), c_centroids))[1]).1 AS cluster,
  -- (4) previous centroid for point
  (arraySort(c -> (c.2), arrayMap(x -> (x.1, L2Distance(x.2, vector)), c_p_centroids))[1]).1 AS cluster_p,
  -- (5) difference in allocation
  if(cluster = cluster_p, 0, 1) as changed
  FROM points
)

 测试数据集

以上大部分内容都是理论性的。现在让我们看看这些理论是否适用于真实数据集！为此，我们将使用纽约市出租车数据集的一个包含 300 万行的子集，希望聚类结果能更具可比性。要创建并从 S3 插入数据，请执行以下步骤：

CREATE TABLE trips (
  trip_id           UInt32,
  pickup_datetime   DateTime,
  dropoff_datetime  DateTime,
  pickup_longitude  Nullable(Float64),
  pickup_latitude   Nullable(Float64),
  dropoff_longitude   Nullable(Float64),
  dropoff_latitude  Nullable(Float64),
  passenger_count   UInt8,
  trip_distance     Float32,
  fare_amount       Float32,
  extra             Float32,
  tip_amount        Float32,
  tolls_amount      Float32,
  total_amount      Float32,
  payment_type      Enum('CSH' = 1, 'CRE' = 2, 'NOC' = 3, 'DIS' = 4, 'UNK' = 5),
  pickup_ntaname    LowCardinality(String),
  dropoff_ntaname   LowCardinality(String)
)
ENGINE = MergeTree
ORDER BY (pickup_datetime, dropoff_datetime);

INSERT INTO trips SELECT trip_id, pickup_datetime, dropoff_datetime, pickup_longitude, pickup_latitude, dropoff_longitude, dropoff_latitude, passenger_count, trip_distance, fare_amount, extra, tip_amount, tolls_amount, total_amount, payment_type, pickup_ntaname, dropoff_ntaname
FROM gcs('https://storage.googleapis.com/clickhouse-public-datasets/nyc-taxi/trips_{0..2}.gz', 'TabSeparatedWithNames');

特征选择

良好的聚类对于特征选择至关重要，因为它直接影响聚类结果的质量。我们不会在这里详细介绍我们如何选择特征。对于感兴趣的读者，我们在笔记本中包含了相关说明。我们最终得到了以下 points 表：

CREATE TABLE points
(
   `id` UInt32,
   `vector` Array(Float32),
   `pickup_hour` UInt8,
   `pickup_day_of_week` UInt8,
   `pickup_day_of_month` UInt8,
   `dropoff_hour` UInt8,
   `pickup_longitude` Float64,
   `pickup_latitude` Float64,
   `dropoff_longitude` Float64,
   `dropoff_latitude` Float64,
   `passenger_count` UInt8,
   `trip_distance` Float32,
   `fare_amount` Float32,
   `total_amount` Float32
) ENGINE = MergeTree ORDER BY id

为了填充这个表，我们使用了一个 INSERT INTO SELECT 的 SQL 查询，它创建了特征、对它们进行了缩放，并过滤了任何异常值。请注意，我们最终的列也被编码在一个向量列中。

链接的查询是我们生成特征的第一次尝试。我们预计在这方面还有更多工作可以做，可能会产生比所示更好的结果。欢迎提出建议！

一点 Python 代码

我们已经描述了算法中的一次迭代实际上是一个 INSERT INTO SELECT 语句，Materialized View 负责维护质心。这意味着我们需要多次调用这个语句，直到收敛。

我们使用的停止条件是移动到不同质心的点少于 1000 个，也就是说，如果少于 1000 个点移动到了不同的质心，我们就停止。这个检查每 5 次迭代进行一次。

对于特定的 K 值执行 K-Means 的伪代码非常简单，因为大部分工作都是由 ClickHouse 完成的。

def kmeans(k, report_every = 5, min_cluster_move = 1000):
   startTime = time.time()
   # INITIALIZATION QUERY
   run_init_query(k)
   i = 0
   while True:
       # ITERATION QUERY
       run_iteration_query(k)
       # report every N iterations
       if (i + 1) % report_every == 0 or i == 0:
           num_moved = calculate_points_moved(k)
           if num_moved <= min_cluster_move:
               break
       i += 1
   execution_time = (time.time() - startTime))
   # COMPUTE d^2 ERROR
   d_2_error = compute_d2_error(k)
   # return the d^2, execution time and num of required iterations
   return d_2_error, execution_time, i+1

完整的代码，包括查询，都在这里下载：【https://github.com/ClickHouse/examples/blob/main/blog-examples/kmeans/kmeans.ipynb#feature-engineering】

选择 K

到目前为止，我们假定 K 值已经确定。确定最优 K 值有几种技术，其中最简单的是计算每个 K 值下每个点与其所属聚类之间的平方距离总和（SSE）。这给了我们一个我们希望最小化的成本指标。方法 compute_d2_error 使用以下 SQL 查询来计算这个值（假设 K 的值为 5）：

WITH 5 as k_val,
(
       SELECT max(iteration)
       FROM centroids WHERE k={k}
) AS c_iteration,
(
   SELECT groupArray((centroid, position))
   FROM
   (
       SELECT
           centroid,
           avgForEachMerge(vector) AS position
       FROM centroids
       WHERE iteration = c_iteration AND k=k_val
       GROUP BY centroid
   )
) AS c_centroids
SELECT
   sum(pow((arraySort(c -> (c.2), arrayMap(x -> (x.1, L2Distance(x.2, vector)), c_centroids))[1]).2, 2)) AS distance
FROM points

这个值保证随着 K 的增加而减小，例如，如果我们将 K 设置为点的数量，每个聚类将有 1 个点，因此我们的错误为 0。不幸的是，这种方法并不能很好地泛化数据！

随着 K 的增加，SSE 通常会减小，因为数据点更接近它们的聚类质心。我们的目标是找到“拐点”，即 SSE 下降速度急剧变化的点。这一点表示增加 K 的收益递减。在拐点处选择 K 提供了一个能捕捉数据中固有分组的模型，而不会过度拟合。识别这个拐点的简单方法是绘制 K vs SSE 曲线并直观地确定值。对于我们的纽约出租车数据，我们测量并绘制了 K 值从 2 到 20 的 SSE：

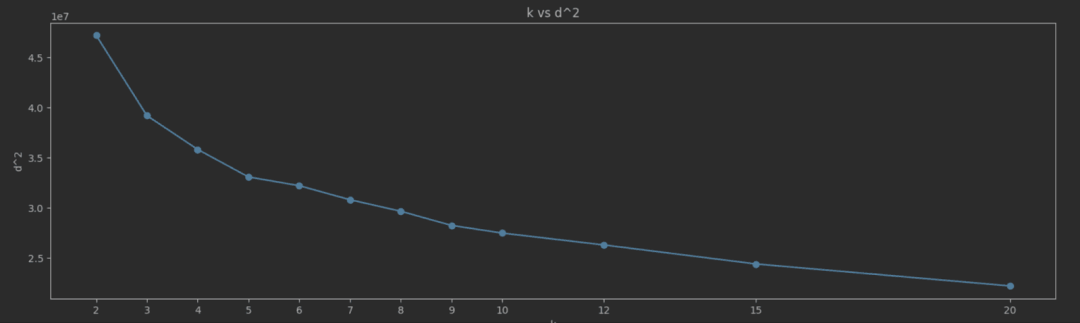
这里的拐点并不像我们希望的那样清晰，但是值为 5 似乎是一个合理的选择。

以上结果基于每个 K 值的单次端到端运行。K-Means 可以收敛到局部最小值，而附近点最终进入同一个聚类的保证是没有的。建议对每个 K 值运行多个值，每次使用不同的初始质心，以找到最佳候选值。

结果

如果我们选择 5 作为 K 的值，算法需要大约 30 次迭代，在一个 12 vCPU 的 ClickHouse Cloud 节点上大约需要 20 秒来收敛。这种方法考虑了每次迭代的所有 300 万行。

k=5
initializing...OK
Iteration 0
Number changed cluster in first iteration: 421206
Iteration 1, 2, 3, 4
Number changed cluster in iteration 5: 87939
Iteration 5, 6, 7, 8, 9
Number changed cluster in iteration 10: 3610
Iteration 10, 11, 12, 13, 14
Number changed cluster in iteration 15: 1335
Iteration 15, 16, 17, 18, 19
Number changed cluster in iteration 20: 1104
Iteration 20, 21, 22, 23, 24
Number changed cluster in iteration 25: 390
stopping as moved less than 1000 clusters in last iteration
Execution time in seconds: 20.79200577735901
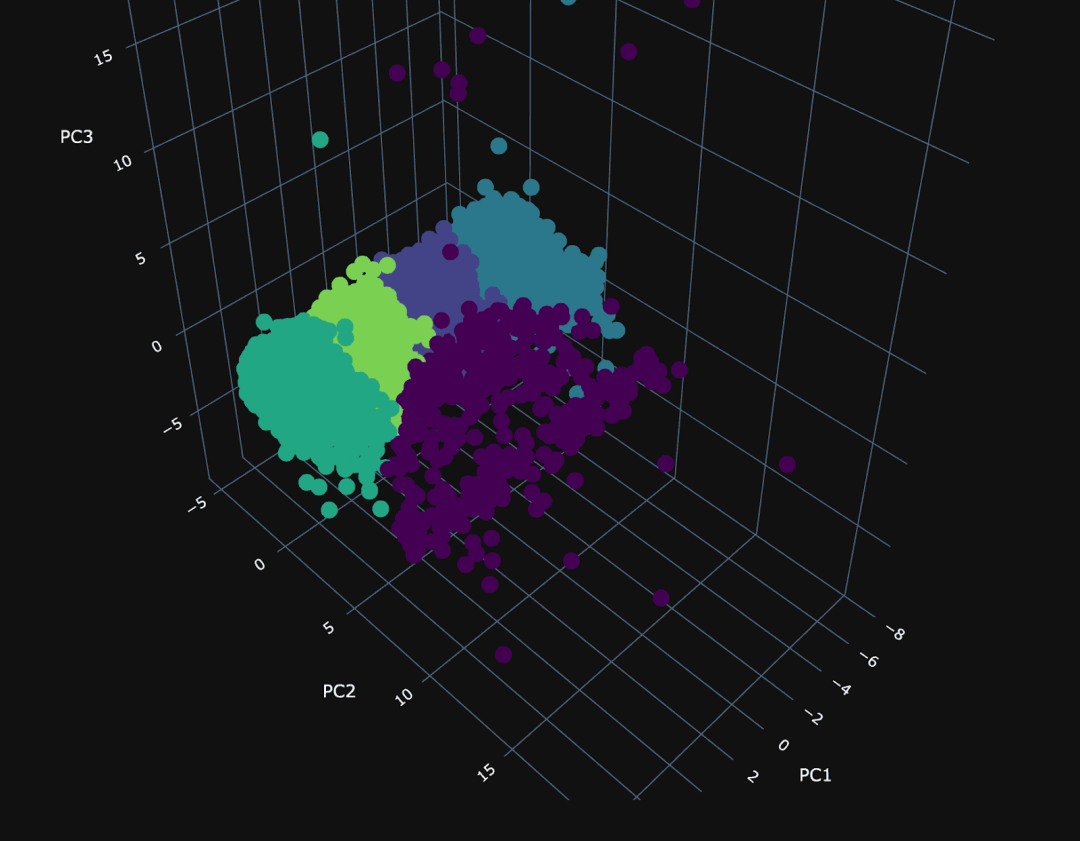
D^2 error for 5: 33000373.34968858

为了展示这些聚类，我们需要降低数据的维度。为此，我们使用了主成分分析（PCA）。我们将 SQL 中的 PCA 实现推迟到另一篇博客中，这里我们只是用 Python 处理了 1 万个随机样本点。通过检查主成分所占方差的比例，我们可以评估 PCA 在捕捉数据基本属性方面的有效性。82% 的方差比例低于通常使用的 90% 的阈值，但对于理解我们的聚类效果已经足够：

Explained variances of the 3 principal components: 0.824

使用我们的 3 个主成分，我们可以绘制相同的随机 1 万个点，并根据其所属的聚类分配不同的颜色。

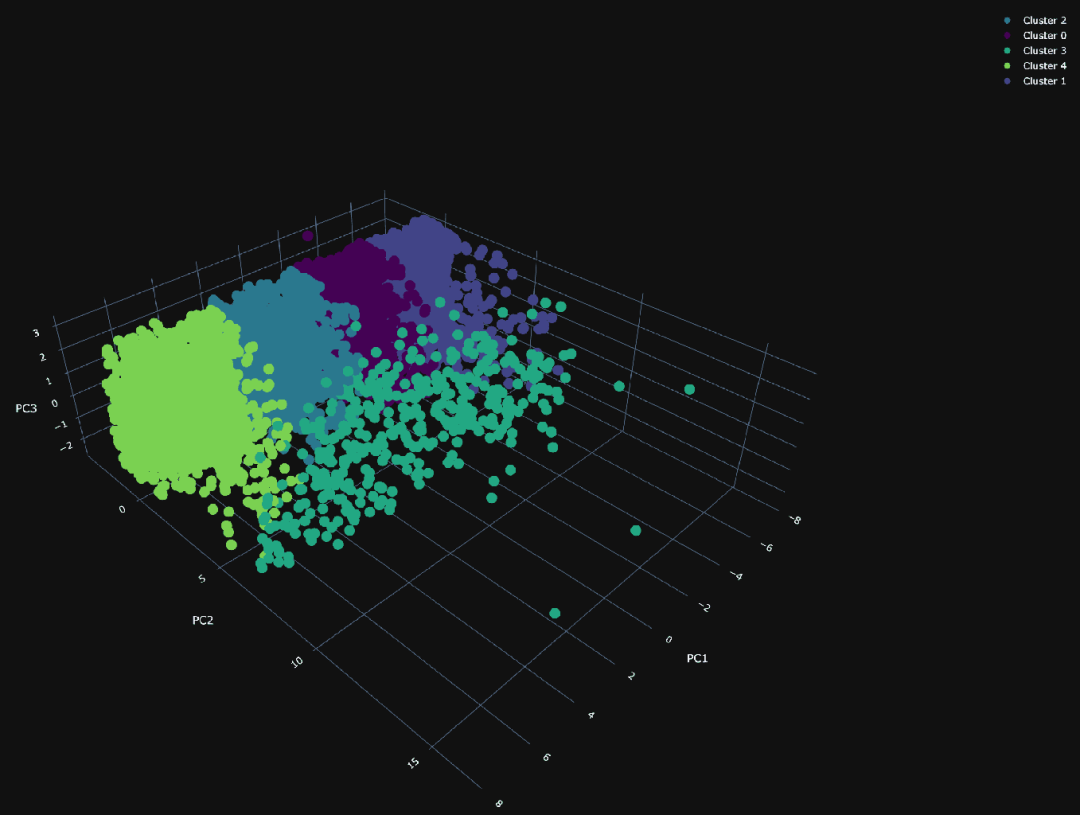
PCA 聚类的可视化呈现出 PC1 和 PC3 之间密集的平面，清晰地分成了四个独立的聚类，暗示着在这些维度上存在着受限的差异。在第二主成分（PC2）上，可视化变得更加稀疏，其中一个聚类（编号为 3）与主要群体偏离，可能具有特别的意义。

为了理解我们的聚类，我们需要标签。理想情况下，我们会通过探索每个聚类中每列数据的分布来生成这些标签，寻找独特的特征和时间/空间模式。我们将尝试用一个 SQL 查询来简洁地理解每个聚类中每列数据的分布。我们应该关注哪些列？可以通过检查 PCA 成分的值并确定主要维度来确定。在笔记本中的代码展示了这一点，并确定了以下内容：

PCA1:: ['pickup_day_of_month: 0.9999497049810415', 'dropoff_latitude: -0.006371842399701939', 'pickup_hour: 0.004444108327647353', 'dropoff_hour: 0.003868258226185553', …]

PCA 2:: ['total_amount: 0.5489526881298809', 'fare_amount: 0.5463895585884886', 'pickup_longitude: 0.43181504878694826', 'pickup_latitude: -0.3074228612885196', 'dropoff_longitude: 0.2756342866763702', 'dropoff_latitude: -0.19809343490462433', …]

PCA 3:: ['dropoff_hour: -0.6998176337701472', 'pickup_hour: -0.6995098287872831', 'pickup_day_of_week: 0.1134719682173672', 'pickup_longitude: -0.05495391127067617', …]

在 PCA1 中，pickup_day_of_month 非常重要，暗示着需要关注月份的时间。在 PCA2 中，维度、上车和下车的位置以及乘车费用似乎是主要贡献因素。这个成分可能专注于特定的行程类型。最后，在 PCA3 中，行程发生的小时似乎是最相关的。为了了解这些列在时间、日期和价格方面在每个聚类中的差异，我们可以再次使用一个 SQL 查询：

WITH
   5 AS k_val,
   (
       SELECT max(iteration)
       FROM centroids
       WHERE k = k_val
   ) AS c_iteration,
   (
       SELECT groupArray((centroid, position))
       FROM
       (
           SELECT
               centroid,
               avgForEachMerge(vector) AS position
           FROM centroids
           WHERE (iteration = c_iteration) AND (k = k_val)
           GROUP BY centroid
       )
   ) AS c_centroids
SELECT
   (arraySort(c -> (c.2), arrayMap(x -> (x.1, L2Distance(x.2, vector)), c_centroids))[1]).1 AS cluster,
   floor(avg(pickup_day_of_month)) AS pickup_day_of_month,
   round(avg(pickup_hour)) AS avg_pickup_hour,
   round(avg(fare_amount)) AS avg_fare_amount,
   round(avg(total_amount)) AS avg_total_amount
FROM points
GROUP BY cluster
ORDER BY cluster ASC

┌─cluster─┬─pickup_day_of_month─┬─avg_pickup_hour─┬─avg_fare_amount─┬─avg_total_amount─┐
│     0 │                11  │            14    │            11  │             13 │
│     1 │                 3   │            14    │            12  │             14 │
│     2 │                18  │            13    │            11  │             13 │
│     3 │                16  │            14    │            49  │             58 │
│     4 │                26  │            14    │            12  │             14 │
└─────────┴─────────────────────┴─────────────────┴─────────────────┴──────────────────┘

9 rows in set. Elapsed: 0.625 sec. Processed 2.95 million rows, 195.09 MB (4.72 million rows/s., 312.17 MB/s.)
Peak memory usage: 720.16 MiB.

第三个聚类明显与更昂贵的行程相关。由于行程费用与一个主要成分相关，该成分还将上车和下车位置确定为关键因素，因此这些可能与特定的行程类型相关。其他聚类需要进行更深入的分析，但似乎专注于月度模式。我们可以在地图可视化中仅绘制聚类 3 的上车和下车位置。以下图中，蓝色和红色点分别表示上车和下车位置：

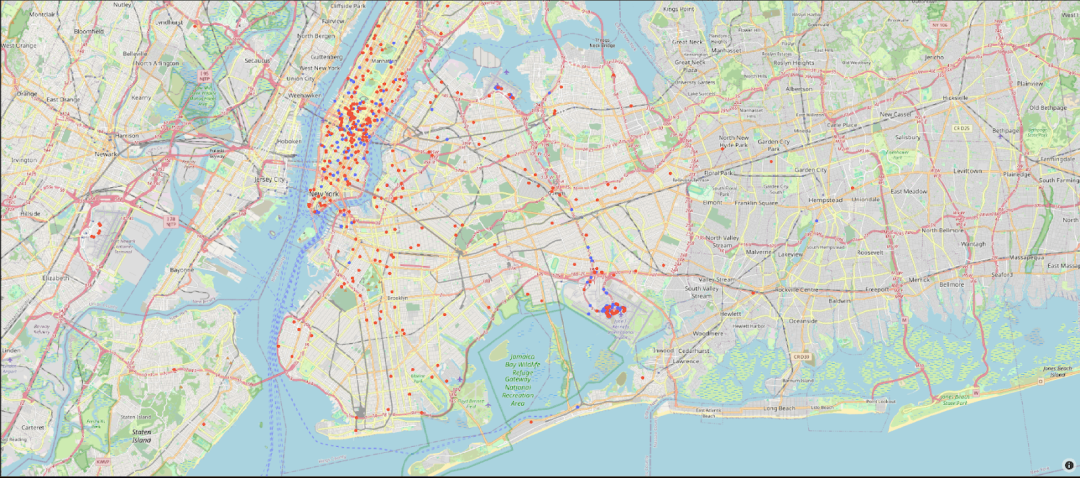
仔细观察地图，可以发现这个聚类与前往和从肯尼迪国际机场的行程相关。

扩展

我们之前的例子仅使用了纽约市出租车行程的 300 万行子集。在更大的数据集上进行测试，即 2009 年的所有出租车行程数据（约 1.7 亿行），我们可以在一个使用 60 个核心的 ClickHouse 服务上，大约在 3 分钟内完成 k=5 的聚类。

k=5
initializing...OK
…
Iteration 15, 16, 17, 18, 19
Number changed cluster in iteration 20: 288
stopping as moved less than 1000 clusters in last iteration
Execution time in seconds: 178.61135005950928
D^2 error for 5: 1839404623.265372
Completed in 178.61135005950928s and 20 iterations with error 1839404623.265372

这产生了与我们之前使用较小子集得到的相似的聚类结果。在一个 64 核的 m5d.16xlarge 上，使用 scikit-learn 运行相同的聚类算法需要 6132 秒，比我们的方法慢了超过 34 倍！在笔记本的末尾可以找到重现这一基准测试的步骤，以及使用 scikit-learn 的方法。

潜在的改进和未来工作

聚类对初始点的选择非常敏感。K-Means++ 是一种改进的 K-Means 聚类方法，通过引入更智能的初始化过程，旨在将初始质心分散开来，减少不良初始质心位置的可能性，从而加快收敛速度，并可能获得更好的聚类效果。我们鼓励读者尝试这一改进。

K-Means 也难以处理分类变量。可以通过独热编码（也可以在 SQL 中实现）以及专门针对这类数据设计的算法，例如 KModes 聚类，来部分解决这个问题。另外，针对特定领域的自定义距离函数，而不仅仅是欧氏距离，也是常见的，并且可以通过用户定义函数（UDFs）来实现。

最后，探索其他软聚类算法也是一个有趣的方向，例如针对正态分布特征的高斯混合模型，或者层次聚类算法，例如凝聚聚类。这些方法也克服了 K-Means 的一个主要限制 - 需要预先指定 K 值。我们期待看到在 ClickHouse SQL 中实现这些算法的尝试！

Meetup 活动讲师招募

我们正为上海活动招募讲师，如果你有独特的技术见解、实践经验或 ClickHouse 使用故事，非常欢迎你加入我们，成为这次活动的讲师，与大家分享你的经验。

点击此处或扫描下方二维码，立刻报名成为讲师！

征稿启示

面向社区长期正文，文章内容包括但不限于关于 ClickHouse 的技术研究、项目实践和创新做法等。建议行文风格干货输出&图文并茂。质量合格的文章将会发布在本公众号，优秀者也有机会推荐到 ClickHouse 官网。请将文章稿件的 WORD 版本发邮件至：Tracy.Wang@clickhouse.com

​​联系我们

手机号：13910395701

邮箱：Tracy.Wang@clickhouse.com

满足您所有的在线分析列式数据库管理需求