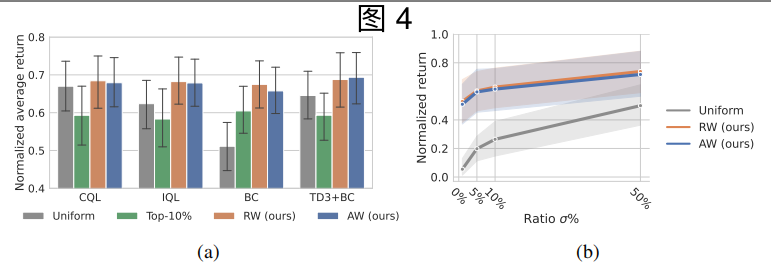
文章目录
- 1.概述
- 2. 查找
- 2.1 查找:算法
- 2.2 查找:理解
- 2.3 查找:实现
- 2.4 查找:语义
- 3. 插入
- 3.1 插入:算法
- 3.2 插入:实现
- 4. 删除
- 4.1 删除:框架
- 4.2 删除:单分支
- 4.3 删除:双分支
1.概述
之前介绍了二叉搜索树的概念和性质可以看到相对其他数据结构,二叉搜索树的特征首先体现在它独特的元素访问方式,也就是寻关键码访问(call by key)。

而所有这类访问无非都是通过三种主要的操作接口完成的,也就是静态查找search,以及动态插入和删除。
接下来讨论,在三个接口的背后分别应该采用什么算法?这些算法又该如何实现?显示的效率又将如何?
2. 查找
2.1 查找:算法
作为最基本操作接口首当其冲自然是查找。
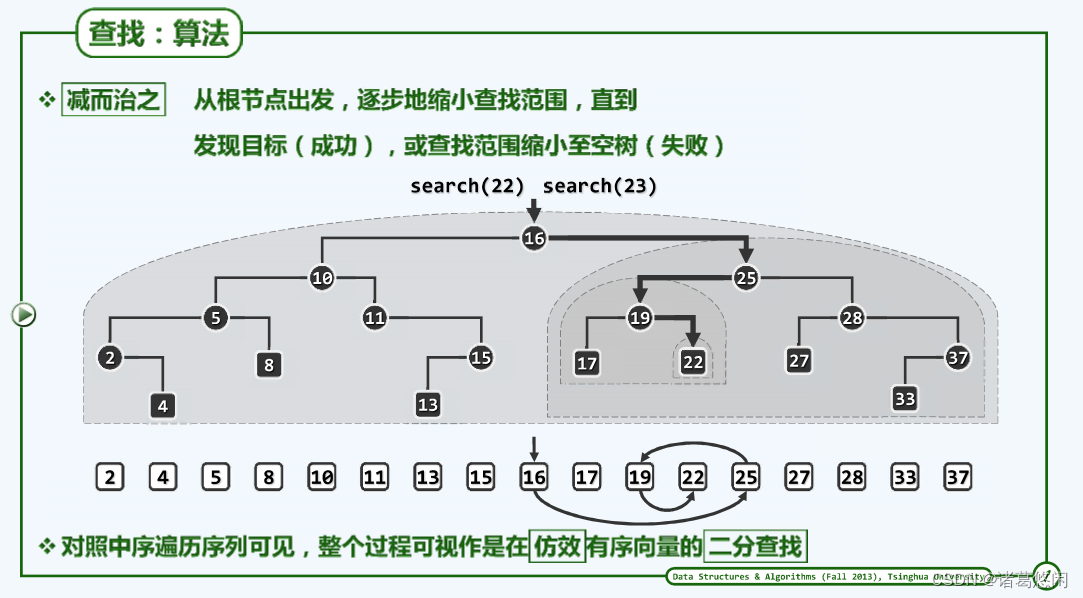
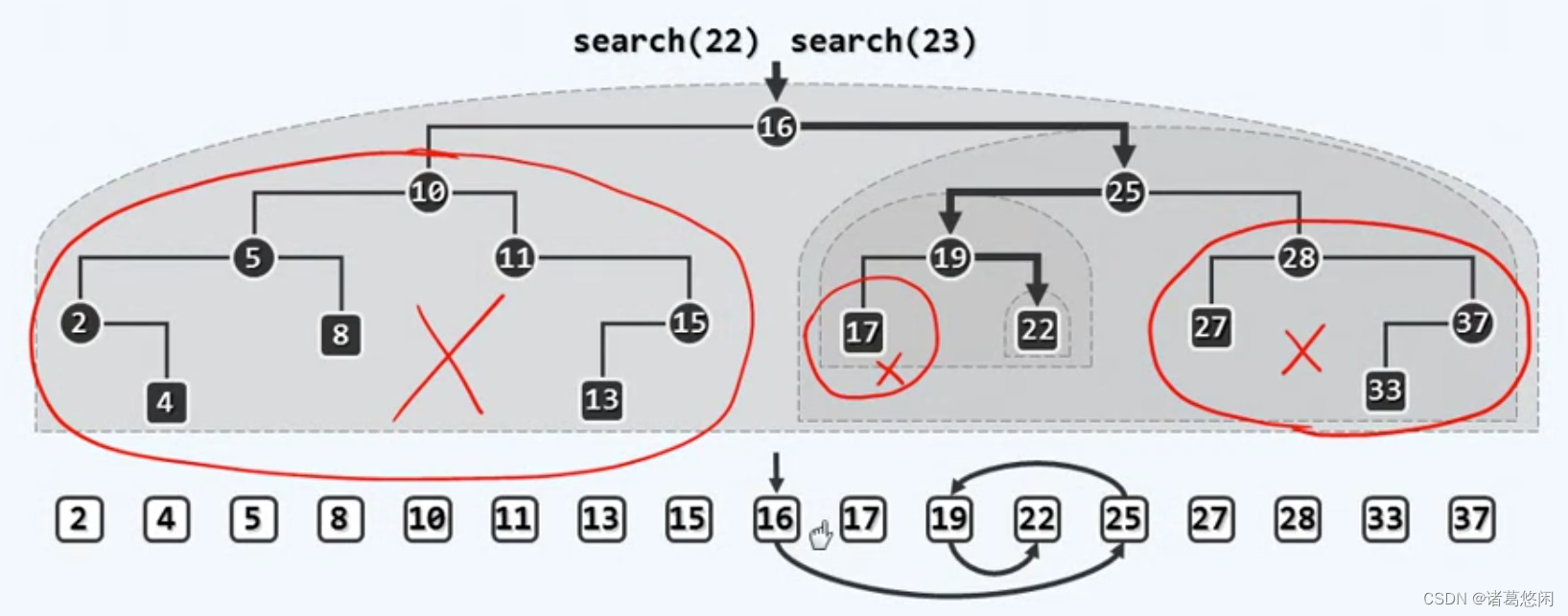
那么如何在BST中查找特定的关键码呢?看上图中具体实例。
首先按照上节推荐方法验证这的确是一棵BST。
~
- 每一次查找都是从根节点开始,假设要查找22,那么首先将目标关键码22与根节点处所对应的关键码16做一比较,不难看出,22相对16更大,那么这样一判断结果意味着什么?应该记得BST所处处具有的顺序性,是的,对于根节点而言它的左后代都不可能比它更大,而当前的查找目标却比它更大,这就意味着根节点的整棵左子树都可以被忽略掉,反过来如果树中的确存有目标关键码22,那么它也必然位于右子树中,因此接下来应相应转入这棵右子树,具体地,也就是将控制权交给这棵子树的树根25。
- 同样的,每当进入一棵子树,都要将目标关键码与当前的子树根节点进行比较,经过这次比较发现目标关键码22相对于子树根节点要更小,那么这意味着什么呢?同样地,根据顺序性节点25的所有右后代都不会比25小,都不可能等于目标关键码22,因此这些节点同样可以被忽略掉,反过来,如果目标关键码的确存在于这棵子树中,那么它也只能存在于其中的左子树中,接下来要顺藤摸瓜转入25的左子树,也就是将控制权交给这棵子树的根节点19。
- 在进入这棵子树之后,同样要将目标关键码22与这棵子树的树根19进行比较,并可以相应忽略掉它的所有左后代,虽然现在只有一个,而将查找范围缩小到这个根节点的右子树,最后一步,在相应进入到这棵右子树之后,同样要将这棵子树的根节点22与目标节点进行比较,终于返现二者相等,至此,这次查找也就相应地以成功而告终。
现在请留意观察在下方列出的这样一个序列,应该看出来这就是这棵BST的中序遍历序列。好的,现在假想地认为它就是一个向量,当然根据全局单调性,它必然是一个有序向量。以下将重新回顾下在这棵BST中刚才的搜索过程,不妨体味一下,这样一个搜索过程在下方的有序向量中对应于怎样的一个过程。
2.2 查找:理解
- 查找首先是对根节点进行一次比较,在有序向量中这对应于以某个轴点为基准进行一次比较,这次比较的结果既可以认为是摒弃掉整棵树的左子树,同时也可以等效地认为是摒弃掉整个向量的左侧子向量,当然也包括根节点以及轴点本身。
- 而接下来所做的决策也就是深入到BST的右子树中,这也可以等效地认为在有序向量中将搜索的范围有效地收缩到它的右子向量中。
- 以下过程只不过是刚才那一步骤在不同程度上的简单重放而已,每一次都会摒弃掉一棵子树或等效的一个子向量,并且深入到对应的另一侧子树或者说另一侧子向量,每次对新的根节点的比较也相当于在向量中对新的轴点进行比较,如此往复,直到最终收缩为仅含一个元素。
其实对于并不存在的关键码所做的查找,虽然会以失败告终,但整个过程相仿。
比如在这棵树中搜索23,依然会在16这个位置向右并且在25这个位置向左再在19这个位置向右,直到最终到22这个位置,依然试图向右,但是此时已经无路可走了。在这样一个情况下,也就是可以判断整个查找失败的时机与成功的查找相比无非增加了最后一次额外的判断而已,本质上没有任何区别。
不难看出,在这个算法的背后,也就是已经熟知的减而治之策略。
具体来说,这里不过是通过一次又一次的比较逐步地缩小整个查找地范围,直至最终抵达平凡的情况。
通过方才对中序遍历序列的比照,也可以看出,整个过程也可以等效地视作是在仿效此前有序向量所行之有效的那种二分查找策略,那么这样一个策略以及查找的过程如何具体实现为代码呢?
2.3 查找:实现
以下给出BST查找算法的一种实现方式

可以看到对外的标准search接口实际上在内部是调用了名为searchIn的一个功能来实现的。
而作为一个更为基本的算法searchIn可以实现如下
具体来说,也就是在以v为根的当前子树中去查找某一个特定的关键码e。作为一个递归函数,首先给出了递归基,比如如果当前子树已经为空,就可以直接返回失败。否则,如果当前根节点与目标关键码正好相等,也就意味着查找成功,无论如何在这种情况下,都可以直接返回。
~
而在一般情况下,也就是子树非空,同时也没有在子树的树根处命中,就继续递归地深入查找,而查找范围在经过一次比较之后,可以相应地确定为究竟是左子树还是右子树。
不难看出,这个算法每递归一次,当前节点v都会下降一层,因此这个算法在最坏情况下地递归深度也不会超过树的高度,这也是这个算法时间复杂度。
2.4 查找:语义
最后再来考察这里地hot参数,作为一个引用型的参数,它总是在这个算法被首次调用时,统一初始化为初值为NULL的内部变量_hot,因此在随后算法的执行过程中,对这个参数的修改,实质上也就是对内部变量_hot的修改,可以看到,对_hot的修改总是发生在每一次试图深入递归之前,具体来说,_hot会记下此前刚刚接受访问的那个非空的节点。
那么总体而言,_hot最终将会指向谁呢?它所对应的语义又是什么呢?
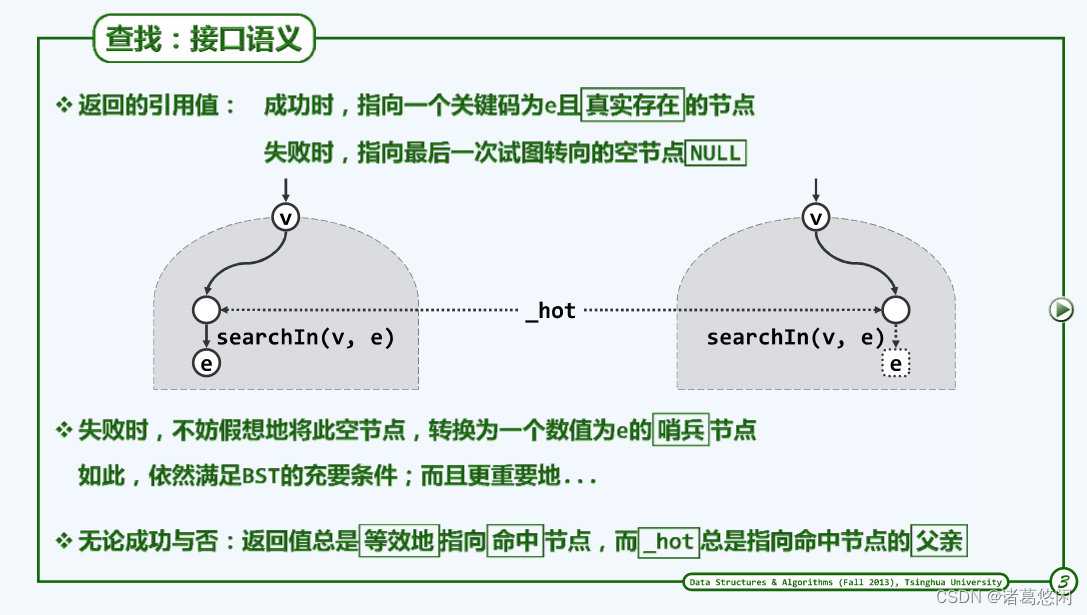
为了便于search接口更加简洁也更加准确地被其他的算法使用,有必要对它的接口语义予以明确地定义,这体现在两个方面。
- 首先这个接口的返回值在不同的情况下,分别对应什么?
这些语义可以通过上图来表示。实际上也无非就是查找成功以及查找失败这两种情况。
~
我们知道,返回值本身也是引用类型的,这里约定在查找成功时返回的引用将指向一个真实存在的节点,而且这个节点恰好与目标关键码相等。而在查找失败时返回的引用将指向一个空节点,这里所说的空节点是指首先它的数值为NULL,但正因为它是一个引用,更确切地讲,此时所返回的那个数值为null的引用。实际上就是在整个查找的过程中最后一步所试图转入的那个数值为空的分支,它指向查找路径末端节点,当前仍不存在的某一个孩子。
- 其次经过这个算法的反复更新,_hot变量的最终取值在各种情况下有对应什么?
在查找成功时,它将指向命中返回节点的父亲。而在失败的时候,它将指向在整个查找过程中最后访问的一个真实存在的节点。
那么如何从语义上将这两种情况下的返回值以及_hot变量统一起来呢?
一种简明的方法就是引入哨兵。是的,在查找失败的时候,可以在末端节点试图转向的那个数值当前为空的引用处增加个假想的哨兵,而且可以进一步的假想着将它的关键码就设置为查找目标。当然不难验证,如果此时的确在这个位置增加一个这样的真实的节点,那么全树依然将是一棵合法的BST。而更有意义的是,在引入了这样一个假想的哨兵之后,就可以从语义上将两种情况统一起来。
具体来说也就是,无论成功与否,返回值总是等效的指向命中节点。尽管在失败情况下,这个命中节点只是假想的,而非真实存在的。而在如此引入了一个假想的哨兵之后,_hot也可以认为总是指向命中节点的父亲。
那么基于这样一个语义明确的search接口插入、删除算法又当如何具体实现呢?
3. 插入
3.1 插入:算法
介绍下BST的插入算法。
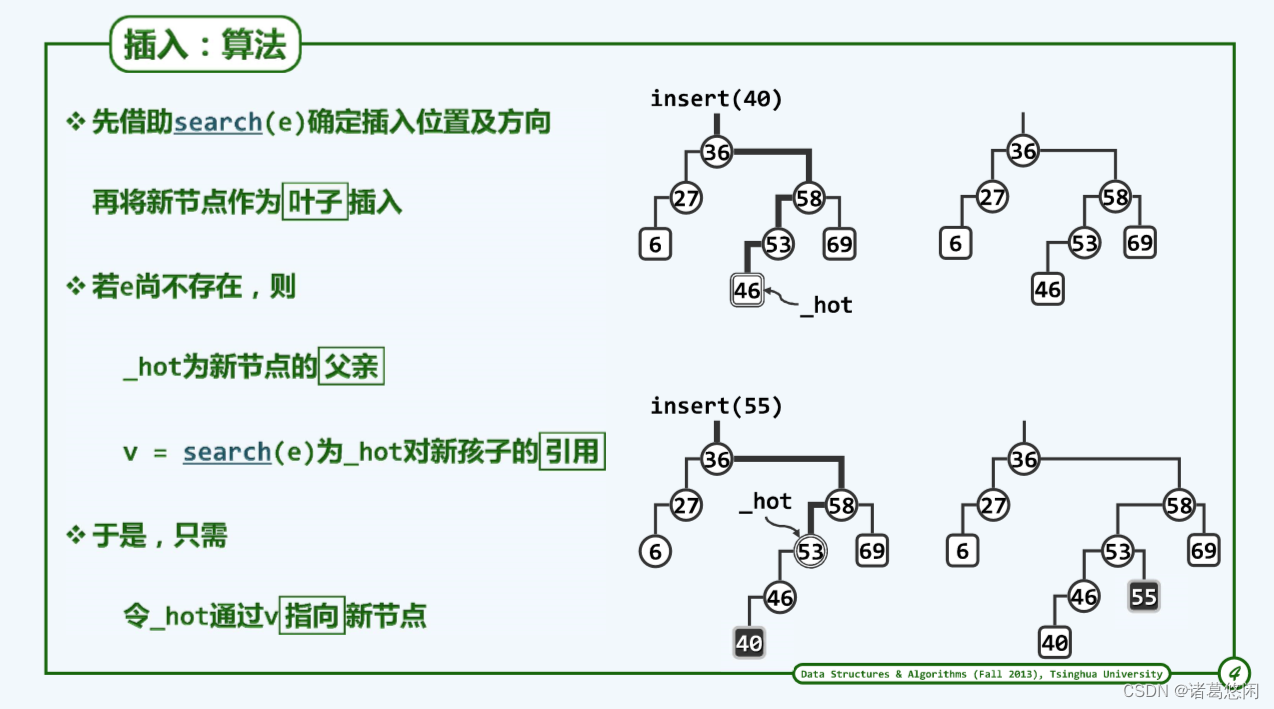
具体来说,如果插入的关键码为e,需要首先调用search接口对它进行定位。既然已经约定禁止雷同元素存在,所以这里不妨假设e还不存在。请注意,此时的search尽管会以失败告终,但_hot变量将会指向查找路径的末端节点,而更重要的是作为返回值_hot的某一个当前仍为空的孩子恰好就是待插入节点应该接入的位置。
来看一个具体的实例
同样地,需要首先确认这是一棵BST,接下来如果需要插入40,就会在search的过程中经过一系列的比较,将查找的范围逐步地收缩,直至最终失败于46。请注意,在此时_hot指向的就是这个46,而此时search的返回值恰好就是46当前为NULL的那个左孩子引用,因此只需将待插入的关键码封装为一个节点,并且令46对应的那个孩子引用改为指向这个新节点,即可完成这次插入操作。插入之后就像上图右上方所示。
~
进一步假设需要再插入55,同样地,经过一系列的搜索,最终失败于53。请注意,尽管此时53的左孩子是存在的,但是根据55和53的大小,在这个位置最终试图转向的是它的右孩子,只不过右孩子当前为空,所以search返回的恰好就是53这个当前为空的右孩子引用,而根据此前所做的统一语义约定,在此时_hot指向的恰好就是53,因此同样地,只需将待插入的55封装为节点,并且令53原先为空的那个孩子引用,改为指向这个新节点,也可以顺利地完成一次插入操作。新插入的节点以及此后所对应的BST就是上图右下方的图。
既然每个新节点所插入的位置在此前都是为空,所以在插入之后,它们也必然是叶子,这也是为什么它们都被画作方形而不是圆形。
好了,接下来的问题自然就是这样一个插入过程如何体现为具体代码呢?
3.2 插入:实现
BST的插入算法可以具体地实现如下

首先针对目标进行一次查找,而且按照约定,这里会忽略掉雷同的元素。也就是说,算法的确会终止于_hot,而返回一个名为x数值为空的引用,所以接下来只需创建一个关键码为e的新节点,并且将_hot作为它的父亲。没错,创建一个以e为关键码的新节点,并且以_hot作为父亲。同时还需要通过这个赋值语句令x不再为空,而改为指向这个新创建的节点(完成节点的双向连接),至此就完成了新创建的这个节点与原树的正确连接。当然接下来还需要更新这棵树的规模,以及新节点历代祖先的高度。
这个代码虽然简单,但是它可以处理各种边界情况。
那么如此实现的insert接口累计的时间复杂度是多少呢?答案是O(h)
不难看出,时间消耗主要集中在两个方面,也就是search以及updataHeightAbove,而且这二者在最坏情况下都不会超过整棵树的高度。因此,总体而言,算法的时间复杂度不过O(h)。
4. 删除
4.1 删除:框架
相对于节点插入操作,BST的节点删除操作要略微复杂一些,在此不妨先给出整个算法的主题框架

可以看到,首先也需要针对目标做一次查找定位,而且与插入操作正好对称,这里需要忽略的是元素尚不存在的情况,反过来,如果这个元素的确存在,就会调用一个名为removeAt的内部例程来真正地实施删除。当然接下来同样要更新全树的规模,同时更新相关祖先的高度。
就运行时间而言,如果暂时忽略掉removeAt接口,整个算法时间消耗依然主要集中于search以及updateHeightAbove这两个例程,所以同样地,这些时间累计而言也不会超过全树的高度O(h)。
那么接下来的问题就是removeAt可能需要处理哪几种情况?各种情况又当如何具体应对呢?
4.2 删除:单分支
先来考虑第一种情况,这也是相对而言更为简单的一种情况。
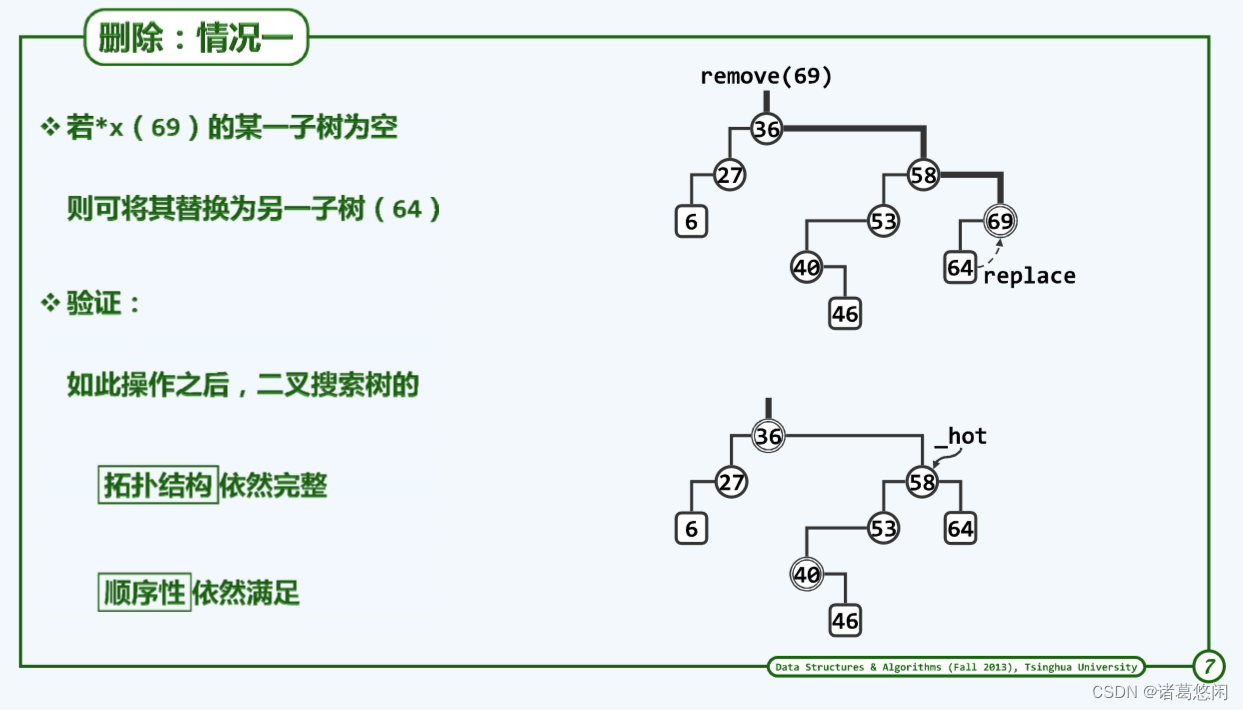
它的特征是经过查找所确定的那个目标节点x至多只有一个孩子,或者反过来,它至少有某棵子树是空的。
比如在这样一棵BST中上图中最上方图,如果试图删除其中的69,那么经过逐层地不断深入,最终的确可以定位到69,而且会发现69至多只有一个孩子,此时只需将这个节点大胆地删除掉,并且取而代之以它那个非空地孩子,在这里也就是64,不难验证,经过这样的处理之后整颗BST依然是一棵名副其实的BST。
因此接下来,不妨将这种情况下的处理方法整理并且实现为具体的代码,比如下面就是一种可能的实现方式。

在这个名为removeAt的算法中,要删除的对象是以x指示的那个节点,请注意,在此前经过搜索所确定的hot也会作为参数传入。接下来需要进行判断,如果x的左孩子并不存在,那么只需直接用它的右孩子来代替,新近提升一层的节点。对称地,如果当前节点没有右孩子,也可以直接用左孩子来代替。这也就是刚刚所说的第一种情况。
~
需要特别指出的是其实这两种情况还涵盖了一种非常特殊的情况,也就是左右孩子可能同时为空,针对这种特殊情况,它依然是能够正确处理。
经过这样的替换操作之后,新进提升一层的节点还需要与它此前的祖父完成直接的连接,这也是以下这两句所完成的任务。至此,情况一的处理已经完全结束。
当然接下来比较棘手的是互补的那种情况,也就是尽管删除的目标存在但是它的左右孩子同时存在,情况一的策略在这种情况下无法直接套用,那么面对这种情况,又当如何处置呢?
4.3 删除:双分支
在这里需要再次使用计算机科学中的法宝,也就是化繁为简,具体来说,要将比较棘手的第二种情况有效地转化为第一种情况。
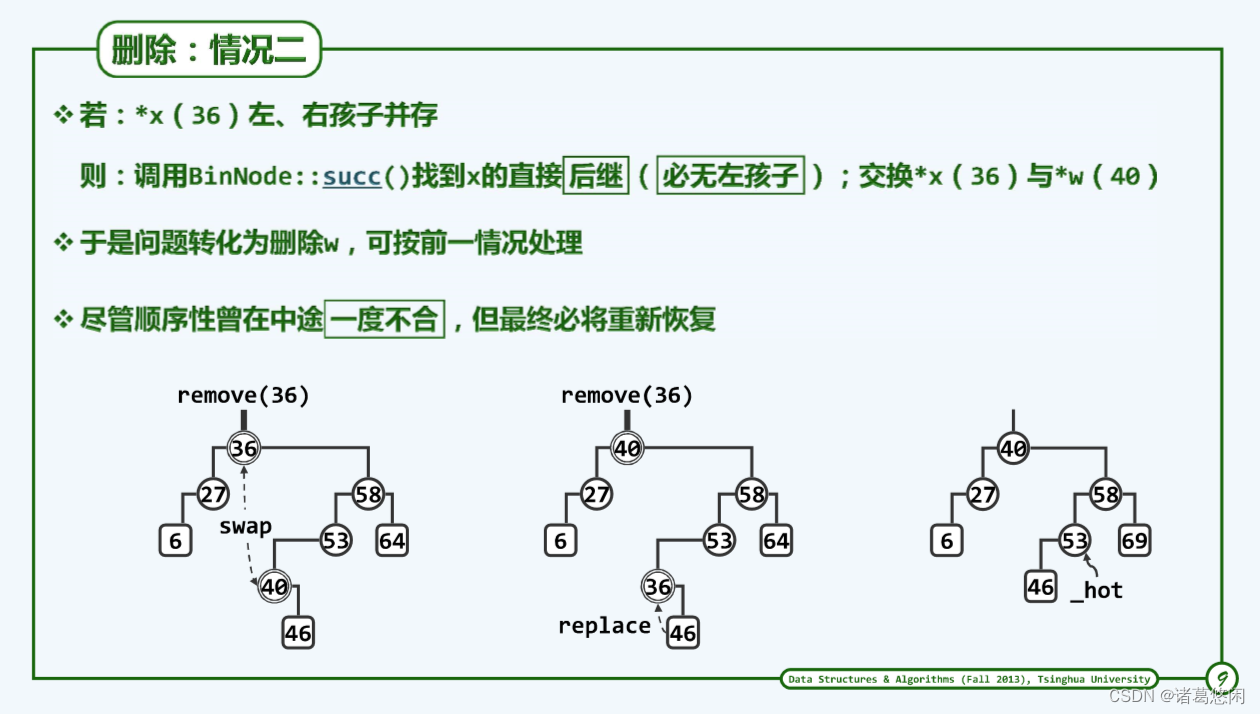
以上左图中的一棵BST为例,假设需要删除节点36,可以看到这个节点的确是比较棘手的情况,因为它的左右后代都存在,此时不妨找到它的直接后继。
应该记得在实现二叉树的时候,对于BinNode类型曾经实现一个名为succ接口。应该记得它的功能与语义,没错,就是返回当前节点在中序遍历下的直接后继。
~
具体来说,也就是在全树中寻找不小于当前节点的最小节点,回顾当时的succ算法,在当前节点拥有右后代情况下算法将首先进入到它所对应的右子树,然后在右子树中沿着左侧分支不断地下行,直到最终不能下行,而整个过程最终所抵达地节点就应该是当前节点地直接后继。
对于这个例子而言36地直接后继就是40,那么接下来可以用当前节点36与它的直接后继40互相兑换,比如对这个例子而言,兑换后的状态就是上中图。
可能会有点担心,因为此时的这棵树在36位置违反了顺序性,它已经不再是一棵BST。是的,担心非常有道理,但是其实大可不必,因为这样一个状态只是一个瞬态,马上就会使它成为一棵BST,而且能够将目标节点删除。是的,此时已经可以着手对目标节点实施删除了,难道不是吗?
稍加观察不难发现,此时的局部(36,46)已经转化为此前的第一种情况,也就是说待删除36至多只有一个孩子,更确切地讲它只有右孩子,为什么它没有左孩子呢?因为作为此前节点地直接后继,它必然是某条左侧分支地末端,自然没有左孩子喽。既然如此,可以直接沿用此前第一种情况的处理手法,也就是用待删除节点36的右孩子46去顶替36,可以得到上右图。
此时,不难验证这棵树已经恢复成一棵不择不扣的BST。
需要特意说明的是,在此后还需要令内部_hot变量指向刚刚被实际删除的节点的父亲,并且从53开始不断地向上追溯历代祖先,因为这些祖先的高度有可能因为刚才后代36的删除而发生变化。
那么同样地,这样一颗化繁为简并且顺利处理的过程如何描述并且实现为具体代码呢?

还是回到刚刚尚未完成的removeAt算法,来补充对第二种情况的处理方法。
按照刚才的分析,只需要找出当前节点的直接后继,并且令这两个节点数据互换,从而等效地将待删除节点转移至新的位置,而且这个位置至多只有一个分支,当然这个分支只可能是右孩子,要将待删除节点顶替为右孩子,只需在这个右孩子以及它此前的祖父之间正确地完成一次双向连接。
- 复杂度
好了,那么作为remove算法地有机部分,这个removeAt算法,它的时间复杂度又是多少呢?是否会超过remove原有的O(h)复杂度呢?
幸好不会,原因在于removeAt本身并不包含任何循环,而其中唯一可能引起复杂度的无非是在第二种情况下对succ()接口的调用,而按照此前的实现方法以及分析结论,这个接口所需要的时间,这个接口所需要的时间也不会超过全树的高度O(h)。
至此,可以得出结论BST的删除操作与插入操作一样,在最坏情况下所需要的时间不会操作全树当时的高度h。
那么这个结论是好,还是不足够好呢?后面将针对这个问题做进一步的探讨。