第十九天,二叉树part06,二叉树的道路任重而道远💪
目录
530.二叉搜索树的最小绝对差
501.二叉搜索树中的众数
236.二叉树的最近公共祖先
总结
530.二叉搜索树的最小绝对差
文档讲解:代码随想录二叉搜索树的最小绝对差
视频讲解:手撕二叉搜索树的最小绝对差
题目:

学习:
如果本题是普通二叉树,可以采取任意一种遍历方式,把二叉树的各节点数值保存在数组中,然后对数组进行排序,最后找到两不同节点之间的最小差值即可。
但本题是二叉搜索树,依据二叉搜索树的特点,对二叉搜索树进行中序遍历,得到的会是一个单调递增的序列,这样无需排列,就能够找到最小差值。
代码:
//时间复杂度O(n)
//空间复杂度O(n)
class Solution {
private:
vector<int> vec;
void traversal(TreeNode* root) {
if (root == NULL) return;
traversal(root->left);
vec.push_back(root->val); // 将二叉搜索树转换为有序数组
traversal(root->right);
}
public:
int getMinimumDifference(TreeNode* root) {
vec.clear();
traversal(root);
if (vec.size() < 2) return 0;
int result = INT_MAX;
for (int i = 1; i < vec.size(); i++) { // 统计有序数组的最小差值
result = min(result, vec[i] - vec[i-1]);
}
return result;
}
};上述方法需要把二叉树所有节点保存在数组中,但事实上我们在进行中序遍历的过程中,就可以进行比较了,方法和98.验证二叉搜索树中使用的相同,可以使用双指针法,一个指针是当前遍历的节点,一个指针是当前节点的前驱节点。再设置一个int型result变量,用来接收最小值,之后除第一个节点外,每次遍历的时候都进行相减并比较,更新最小值。
代码:中序遍历(递归法)
//时间复杂度O(n)
//空间复杂度O(n)
class Solution {
public:
int minnum = INT_MAX;
TreeNode* pre = nullptr; //表示前一个节点
//二叉搜索树,采用中序遍历的方式,得到的是一个递增序列
void traversal(TreeNode* root) {
if(root == nullptr) return;
traversal(root->left);
if(pre != nullptr) {
minnum = min(root->val - pre->val, minnum);
}
pre = root;
traversal(root->right);
}
int getMinimumDifference(TreeNode* root) {
traversal(root);
return minnum;
}
};代码:中序遍历(迭代法)
//时间复杂度O(n)
//空间复杂度O(n)
class Solution {
public:
//迭代法,采用中序遍历
int getMinimumDifference(TreeNode* root) {
//创建一个栈存储节点
stack<TreeNode*> st;
//双指针,分别指向中序遍历过程中的前后节点
TreeNode* cur = root;
TreeNode* pre = nullptr;
int result = INT_MAX;
while(cur != nullptr || !st.empty()) {
if(cur != nullptr) {
st.push(cur);
cur = cur->left; //左
}
else {
cur = st.top();
st.pop();
if(pre != nullptr) { //中
result = min(cur->val - pre->val, result);
}
pre = cur;
cur = cur->right; //右
}
}
return result;
}
};总结:在遇到二叉搜索树时,要时刻牢记二叉搜索树的特点。无论是求最值,求差值还是作前后节点比较,都要思考一下二叉搜索树是有序的,要利用好这一特点。
501.二叉搜索树中的众数
文档讲解:代码随想录二叉搜索树中的众数
视频讲解:手撕二叉搜索树中的众数
学习:
同样如果本题不是二叉搜索树,只是一个普通树的话。本题可以采取的方式是,通过任意一种遍历方法,把二叉树中各节点的值保存下来。要注意这里需要统计每个数出现的频率,因此可以采用map的数据结构,且为了存储方便,可以采用哈希表的方式,让每次重复插入的时候,查找效率为O(1),key设置为节点值,value设置为频率。统计完后,再将他们放入数组中,并进行排序即可。(本题使用到了一个新的排序方法,是sort()算法内复用的)
代码:
class Solution {
private:
void searchBST(TreeNode* cur, unordered_map<int, int>& map) { // 前序遍历
if (cur == NULL) return ;
map[cur->val]++; // 统计元素频率
searchBST(cur->left, map);
searchBST(cur->right, map);
return ;
}
bool static cmp (const pair<int, int>& a, const pair<int, int>& b) {
return a.second > b.second;
}
public:
vector<int> findMode(TreeNode* root) {
unordered_map<int, int> map; // key:元素,value:出现频率
vector<int> result;
if (root == NULL) return result;
searchBST(root, map);
vector<pair<int, int>> vec(map.begin(), map.end());
sort(vec.begin(), vec.end(), cmp); // 给频率排个序
result.push_back(vec[0].first);
for (int i = 1; i < vec.size(); i++) {
// 取最高的放到result数组中
if (vec[i].second == vec[0].second) result.push_back(vec[i].first);
else break;
}
return result;
}
};但本题是线索二叉树, 节点之间是有序的,并且力扣上本题也希望我们使用除递归以外的额外空间开销(空间复杂度为O(1)),因此本题需要从线索二叉树的特点上入手。
- 由于是线索二叉树,并且本题中的二叉树内各节点的值是能够重复的,因此对其进行中序遍历,得到的是一个非递减序列,同时相同值的节点会依次排序。
- 我们需要统计的是值相同的点的个数,并且不使用大于O(1)的空间复杂度,因此我们需要在遍历的过程中,就把值给统计出来,并且把频率大的数加入到返回数组中(注意返回值不参与空间复杂度)。
- 我们可以使用两个int型变量count和maxconut,一个用来统计当前数的频率,一个用来统计最大频率。每次遍历过程中比较count和maxcount。如果count小于maxcount则继续遍历。如果count和maxcount相等,则将当前的数加入到答案数组中。如果count大于maxcount,则说明此时需要更新最大频率了,要注意的是此时不仅要更改maxcount的值,还需要将返回数组清零,因为此时数组内的数不再是最大频率的数了,而我们只需要最大频率的数,因此需要将返回数组清零,并重新将当前数加入到返回数组中。
代码:
//时间复杂度O(n)
//空间复杂度O(1)(除去递归带来的隐式空间复杂度)
class Solution {
public:
vector<int> result;
int maxcount = 0; //存储最大频率
int count = 0; //当前频率
TreeNode* pre = nullptr; //指向当前节点的前一个节点
//递归法,中序遍历
//确定返回值和参数列表,本题需要遍历所有节点,因此参数为root,本题采用全局遍历vector存储结果,因此不需要返回值。
void traversal(TreeNode* cur) {
if(cur == nullptr) return;
traversal(cur->left); //左
//中
if(pre == nullptr) { //第一个节点
count = 1;
}
else if (pre->val == cur->val) { //与上一个节点数值相同
count++;
}
else { //与上一个节点数值不同
count = 1;
}
pre = cur; //更新上一个节点
if (count == maxcount) { //如果和最大统计频率一样
result.push_back(cur->val);
}
if (count > maxcount) { //更新最大频率,每次出现更大频率的数时,要将答案数组清理
maxcount = count;
result.clear();
result.push_back(cur->val);
}
traversal(cur->right);
return;
}
vector<int> findMode(TreeNode* root) {
traversal(root);
return result;
}
};236.二叉树的最近公共祖先
文档讲解:代码随想录二叉树的公共祖先
视频讲解:手撕二叉树的最近公共祖先
题目:


学习:依据本题题干和提示,需要找到两个节点的最近公共祖先,且两个节点必定存在于二叉树当中。显然本题需要遍历二叉树的所有节点,那么采取什么遍历方式比较好呢,由于本题要找到的是节点p、q的最近公共祖先,因此应该自底向上进行查找,当找到节点p或q后就把当前节点的信息返回给父节点,然后再逐级返回,这种遍历方式显然应该采用后序遍历。
本题递归三部曲的设置十分重要,我们可以通过下图来总结进行递归三部曲的设置:
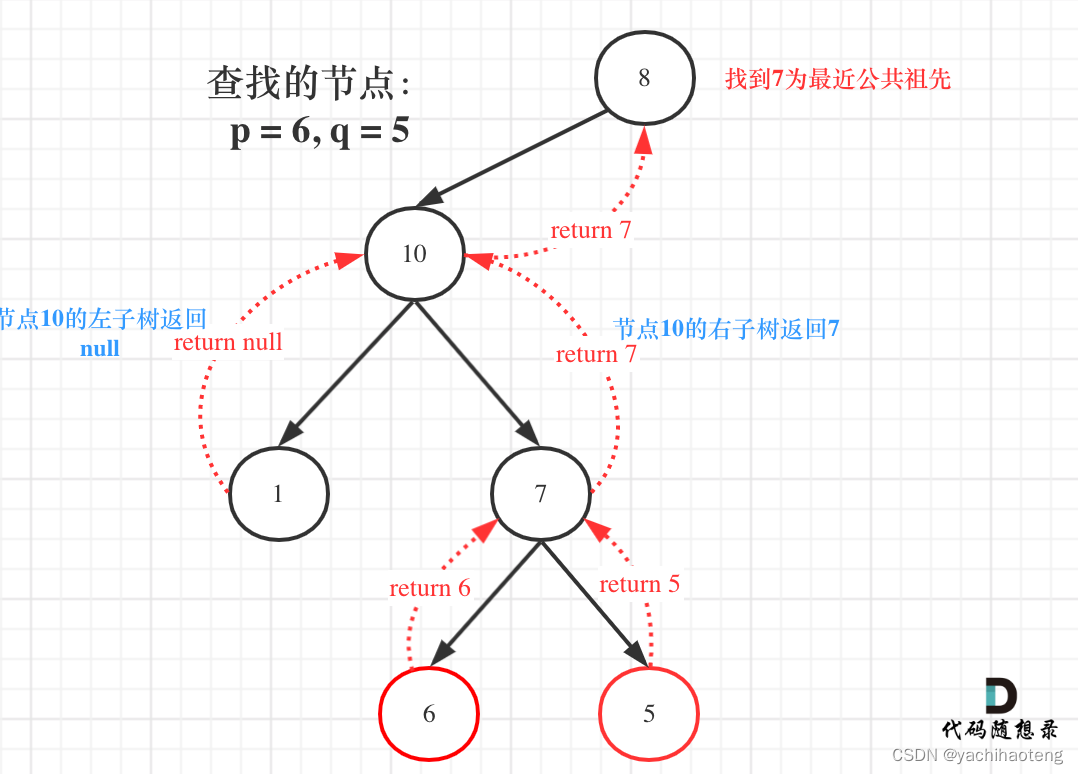
1.确定返回值和参数:本题需要我们返回最近公共祖先的节点,因此本题返回值类型因改为TreeNode*,参数则因为需要遍历二叉树,因此传入root。
TreeNode* lowestCommonAncestor(TreeNode* root, TreeNode* p, TreeNode* q)2.确定终止条件:当节点为nullptr或者节点等于p或q时,我们将节点进行返回。
//确定终止条件
if(root == NULL) return NULL;
if(root->val == p->val || root->val == q->val) return root;3.确定单层递归逻辑:当当前节点不是目标节点也不是空节点时,说明我们需要向下遍历了,且我们还需要设置两个TreeNode* 变量来接受左右子树遍历的结果。
//确定单层递归逻辑
//采取后续遍历的方式
TreeNode* left = lowestCommonAncestor(root->left, p, q);
TreeNode* right = lowestCommonAncestor(root->right, p, q);4.最后我们根据返回结果的四种情况进行判断和上层返回:
//四种情况
if(left != NULL && right != NULL) return root; //左右子树都有目标值(由于目标值是不同的,且二叉树内没有相同的值,因此肯定是p、q都找到了)
else if (left != NULL && right == NULL) return left; //有可能公共祖先已经找到了,并且由于右子树没有目标节点,说明当前子树不可能是公共祖先,因此返回上一个结果。
else if (left == NULL && right != NULL) return right;
else return NULL;注意:本题是包含了p节点是q节点祖先,或者q节点是p节点祖先的情况的,因为如果p节点是q节点的祖先,那我们在遍历过程中,遍历到p节点就返回了,不会继续向下遍历,虽然这样不能遍历到q节点但是我们会把p节点一直往上返回最后输出。又由于本题中的条件p、q节点一定存在,因此我们就可以断定返回上来的p节点一定是q节点的祖先。
代码:
//时间复杂度O(n)
//空间复杂度O(n)
class Solution {
public:
TreeNode* lowestCommonAncestor(TreeNode* root, TreeNode* p, TreeNode* q) {
//确定终止条件
if(root == NULL) return NULL;
if(root->val == p->val || root->val == q->val) return root;
//确定单层递归逻辑
//采取后续遍历的方式
TreeNode* left = lowestCommonAncestor(root->left, p, q);
TreeNode* right = lowestCommonAncestor(root->right, p, q);
//四种情况
if(left != NULL && right != NULL) return root; //左右子树都有目标值(由于目标值是不同的,且二叉树内没有相同的值,因此肯定是p、q都找到了)
else if (left != NULL && right == NULL) return left; //有可能公共祖先已经找到了,并且由于右子树没有目标节点,说明当前子树不可能是公共祖先,因此返回上一个结果。
else if (left == NULL && right != NULL) return right;
else return NULL;
}
};总结:
- 求最小公共祖先,需要从底向上遍历,那么二叉树,只能通过后序遍历,通过回溯实现从底向上的遍历方式。
- 在回溯过程中,还需要不断比较底层递归上来的结果,也就是left和right并进行逻辑判断。
- 要理解为什么left为空,right不为空(或者相反),能够返回right,这本质是因为我们要返回的是查找的结果,只有在找到左右子树都不为空时,此时的第一个节点才是最近公共祖先。否则的话就可能会出现p是q的父节点或者q是p的父节点,或者已经找到了最近公共祖先节点,此时我们就需要不断的把结果进行返回。
总结
今天的题主要练习对二叉搜索树特点的利用,以及对后序遍历和回溯过程的理解。