数据挖掘案例-商品零售购物篮分析

1. 背景与挖掘目标

现代商品种类繁多，顾客往往会由于需要购买的商品众多而变得疲于选择，且顾客并不会因为商品选择丰富而选择购买更多的商品。

例如，货架上有可口可乐和百事可乐，若顾客需要选购可乐若干，或许会同时购买两种可乐，但是购买可乐的数量大多数情况下不会因为品牌数量增加而增加。

繁杂的选购过程往往会给顾客疲惫的购物体验。

对于某些商品，顾客会选择同时购买，如面包与牛奶、薯片与可乐等，当面包与牛奶或者薯片与可乐分布在商场的两侧，且距离十分遥远时，顾客购买的欲望就会减少，在时间紧迫的情况下顾客甚至会放弃购买某些计划购买的商品。相反，把牛奶与面包摆放在相邻的位置，既给顾客提供便利，提升购物体验，又提高顾客购买的概率，达到了促销的目的。

许多商场以打折方式作为主要促销手段，以更少的利润为代价获得更高的销量。

打折往往会使顾客增加原计划购买商品的数量，对于原计划不打算购买且不必要的商品，打折的吸引力远远不足。而正确的商品摆放却能提醒顾客购买某些必需品，甚至吸引他们购买感兴趣的商品。

综合商品零售行业现状、提供的数据，实现以下目标：

构建零售商品的Apriori关联规则模型，分析商品之间的关联性。
根据模型结果给出销售策略。

2. 分析方法与过程

总体流程：

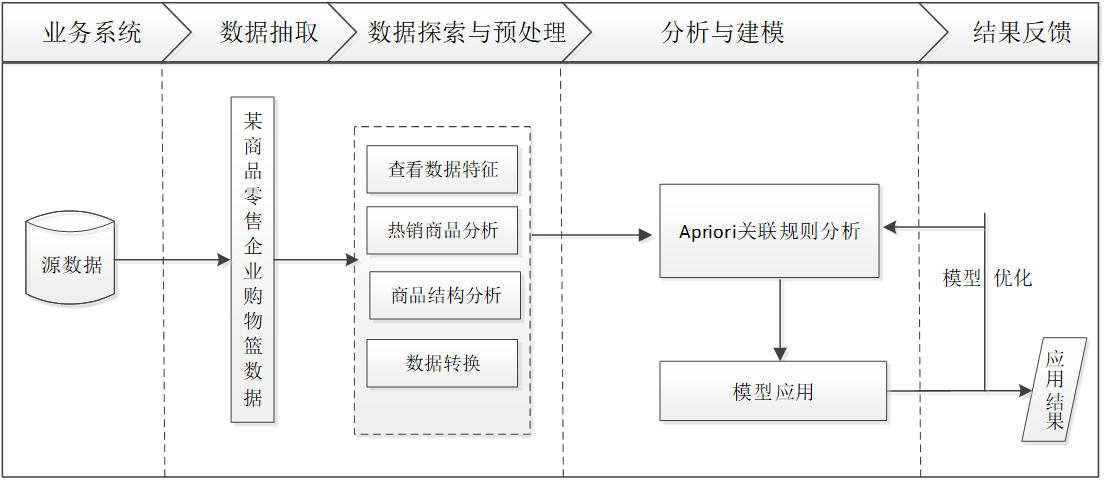
1.对原始数据进行数据探索性分析，分析商品的热销情况与商品结构。

2.对原始数据进行数据预处理，转换数据形式，使之符合Apriori关联规则算法要求。

3.在步骤2得到的建模数据基础上，采用Apriori关联规则算法，调整模型输入参数，完成商品关联性分析。

4.结合实际业务，对模型结果进行分析，根据分析结果给出销售建议，最后输出关联规则结果。

2.1 数据探索分析

探索数据特征是了解数据的第一步。分析商品热销情况和商品结构，是为了更好地实现企业的经营目标。商品管理应坚持商品齐全和商品优选的原则，产品销售基本满足“二八定律”即80%的销售额是由20%的商品创造的，这些商品是企业主要盈利商品，要作为商品管理的重中之重。商品热销情况分析和商品结构分析也是商品管理不可或缺的一部分，其中商品结构分析能够帮助保证商品的齐全性，热销情况分析可以助力于商品优选。

某商品零售企业共收集了9835个购物篮的数据，购物篮数据主要包括3个属性：id、Goods和Types。属性的具体说明如表所示。

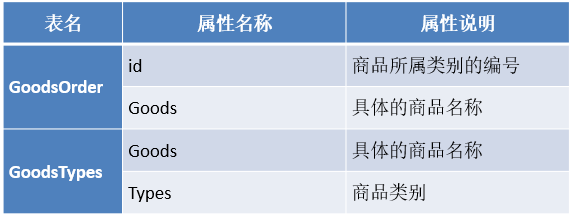
1. 数据特征

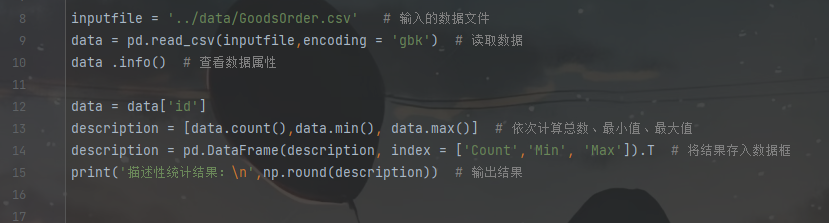
探索数据的特征，查看每列属性、最大值、最小值，是了解数据的第一步。

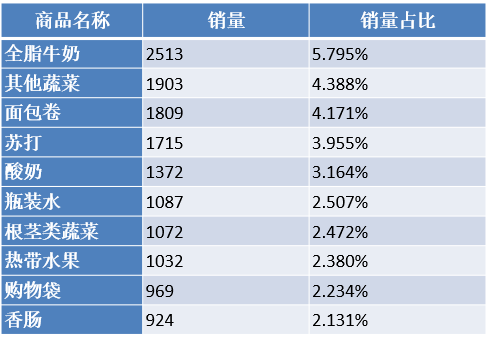
2. 分析热销商品

商品热销情况分析是商品管理不可或缺的一部分，热销情况分析可以助力于商品优选。计算销量排行前10商品的销量及占比，并绘制条形图显示销量前10商品的销量情况。

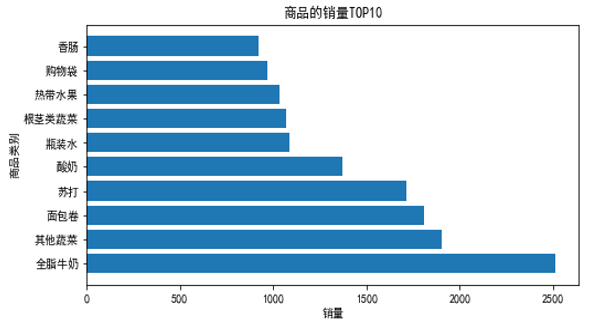
3. 分析商品结构

对每一类商品的热销程度进行分析，有利于商家制定商品在货架的摆放策略和位置，若是某类商品较为热销，商场可以把此类商品摆放到商场的中心位置，方便顾客选购。或者放在商场深处位置，使顾客在购买热销商品前经过非热销商品，增加在非热销商品处的停留时间，促进非热销产品的销量。

原始数据中的商品本身已经过归类处理，但是部分商品还是存在一定的重叠，故再次对其进行归类处理。分析归类后各类别商品的销量及其占比，并绘制饼图显示各类商品的销量占比情况。

通过分析各类别商品的销量及其占比情况可知，非酒精饮料、西点、果蔬三类商品销量差距不大，占总销量的50%左右，同时，根据大类划分发现和食品相关的类的销量总和接近90%，说明了顾客倾向于购买此类产品，而其余商品仅为商场满足顾客的其余需求而设定，并非销售的主力军。

查看销量第一的非酒精饮料类商品的内部商品结构，并绘制饼图显示其销量占比情况。

通过分析非酒精饮料内部商品的销量及其占情况可知，全脂牛奶的销量在非酒精饮料的总销量中占比超过33%，前3种非酒精饮料的销量在非酒精饮料的总销量中占比接近70%，说明了大部分顾客到店购买的饮料为这三种，需要时常注意货物的库存，定期补货必不可少。

2. 2 数据预处理

通过对数据探索分析，发现数据数据完整，并不存在缺失值。建模之前需要建模之前需要转变数据的格式，才能使用apriori函数进行关联分析。

数据转换：

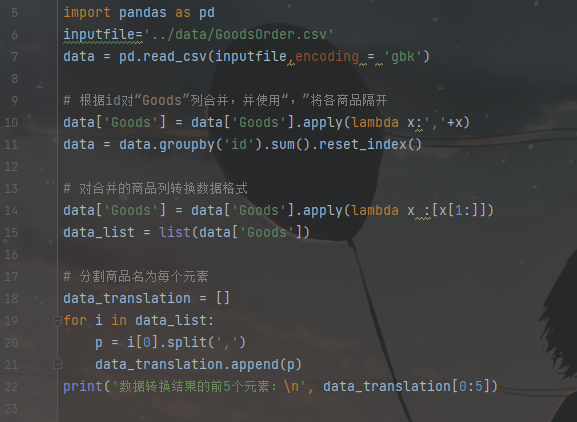
2. 3 模型构建

采用关联规则算法，挖掘它们之间的关联关系。关联规则算法主要用于寻找数据中项集之间的关联关系。它揭示了数据项间的未知关系，基于样本的统计规律，进行关联规则分析。根据所分析的关联关系，可从一个属性的信息来推断另一个属性的信息。当置信度达到某一阈值时，就可以认为规则成立。Apriori算法是常用的关联规则算法之一，也是最为经典的分析频繁项集的算法，第一次实现在大数据集上可行的关联规则提取的算法。除此之外，还有FP-Tree算法，Eclat算法和灰色关联算法等。主要使用Apriori算法进行分析。

1. 商品购物篮关联规则模型构建

模型主要由输入、算法处理、输出3个部分组成。

输入部分包括：建模样本数据的输入；建模参数的输入。
算法处理部分是采用Apriori关联规则算法进行处理。
输出部分为采用Apriori关联规则算法进行处理后的结果。

模型具体实现步骤为：

首先设置建模参数最小支持度、最小置信度，输入建模样本数据；
然后采用Apriori关联规则算法对建模的样本数据进行分析，以模型参数设置的最小支持度、最小置信度以及分析目标作为条件，如果所有的规则都不满足条件，则需要重新调整模型参数，否则输出关联规则结果。

目前，如何设置最小支持度与最小置信度，并没有统一的标准。大部分都是根据业务经验设置初始值，然后经过多次调整，获取与业务相符的关联规则结果。本案例经过多次调整并结合实际业务分析，选取模型的输入参数为：最小支持度0.02、最小置信度0.35。

# -*- coding: utf-8 -*-
from numpy import *
 
def loadDataSet():
    return [['a', 'c', 'e'], ['b', 'd'], ['b', 'c'], ['a', 'b', 'c', 'd'], ['a', 'b'], ['b', 'c'], ['a', 'b'],
            ['a', 'b', 'c', 'e'], ['a', 'b', 'c'], ['a', 'c', 'e']]
 
def createC1(dataSet):
    C1 = []
    for transaction in dataSet:
        for item in transaction:
            if not [item] in C1:
                C1.append([item])
    C1.sort()
    # 映射为frozenset唯一性的，可使用其构造字典
    return list(map(frozenset, C1))     
    
# 从候选K项集到频繁K项集（支持度计算）
def scanD(D, Ck, minSupport):
    ssCnt = {}
    for tid in D:   # 遍历数据集
        for can in Ck:  # 遍历候选项
            if can.issubset(tid):  # 判断候选项中是否含数据集的各项
                if not can in ssCnt:
                    ssCnt[can] = 1  # 不含设为1
                else:
                    ssCnt[can] += 1  # 有则计数加1
    numItems = float(len(D))  # 数据集大小
    retList = []  # L1初始化
    supportData = {}  # 记录候选项中各个数据的支持度
    for key in ssCnt:
        support = ssCnt[key] / numItems  # 计算支持度
        if support >= minSupport:
            retList.insert(0, key)  # 满足条件加入L1中
            supportData[key] = support  
    return retList, supportData
 
def calSupport(D, Ck, min_support):
    dict_sup = {}
    for i in D:
        for j in Ck:
            if j.issubset(i):
                if not j in dict_sup:
                    dict_sup[j] = 1
                else:
                    dict_sup[j] += 1
    sumCount = float(len(D))
    supportData = {}
    relist = []
    for i in dict_sup:
        temp_sup = dict_sup[i] / sumCount
        if temp_sup >= min_support:
            relist.append(i)
# 此处可设置返回全部的支持度数据（或者频繁项集的支持度数据）
            supportData[i] = temp_sup
    return relist, supportData
 
# 改进剪枝算法
def aprioriGen(Lk, k):
    retList = []
    lenLk = len(Lk)
    for i in range(lenLk):
        for j in range(i + 1, lenLk):  # 两两组合遍历
            L1 = list(Lk[i])[:k - 2]
            L2 = list(Lk[j])[:k - 2]
            L1.sort()
            L2.sort()
            if L1 == L2:  # 前k-1项相等，则可相乘，这样可防止重复项出现
                # 进行剪枝（a1为k项集中的一个元素，b为它的所有k-1项子集）
                a = Lk[i] | Lk[j]  # a为frozenset()集合
                a1 = list(a)
                b = []
                # 遍历取出每一个元素，转换为set，依次从a1中剔除该元素，并加入到b中
                for q in range(len(a1)):
                    t = [a1[q]]
                    tt = frozenset(set(a1) - set(t))
                    b.append(tt)
                t = 0
                for w in b:
                    # 当b（即所有k-1项子集）都是Lk（频繁的）的子集，则保留，否则删除。
                    if w in Lk:
                        t += 1
                if t == len(b):
                    retList.append(b[0] | b[1])
    return retList

def apriori(dataSet, minSupport=0.2):
# 前3条语句是对计算查找单个元素中的频繁项集
    C1 = createC1(dataSet)
    D = list(map(set, dataSet))  # 使用list()转换为列表
    L1, supportData = calSupport(D, C1, minSupport)
    L = [L1]  # 加列表框，使得1项集为一个单独元素
    k = 2
    while (len(L[k - 2]) > 0):  # 是否还有候选集
        Ck = aprioriGen(L[k - 2], k)
        Lk, supK = scanD(D, Ck, minSupport)  # scan DB to get Lk
        supportData.update(supK)  # 把supk的键值对添加到supportData里
        L.append(Lk)  # L最后一个值为空集
        k += 1
    del L[-1]  # 删除最后一个空集
    return L, supportData  # L为频繁项集，为一个列表，1，2，3项集分别为一个元素

# 生成集合的所有子集
def getSubset(fromList, toList):
    for i in range(len(fromList)):
        t = [fromList[i]]
        tt = frozenset(set(fromList) - set(t))
        if not tt in toList:
            toList.append(tt)
            tt = list(tt)
            if len(tt) > 1:
                getSubset(tt, toList)
 
def calcConf(freqSet, H, supportData, ruleList, minConf=0.7):
    for conseq in H:  #遍历H中的所有项集并计算它们的可信度值
        conf = supportData[freqSet] / supportData[freqSet - conseq]  # 可信度计算，结合支持度数据
        # 提升度lift计算lift = p(a & b) / p(a)*p(b)
        lift = supportData[freqSet] / (supportData[conseq] * supportData[freqSet - conseq])
 
        if conf >= minConf and lift > 1:
            print(freqSet - conseq, '-->', conseq, '支持度', round(supportData[freqSet], 6), '置信度：', round(conf, 6),
                  'lift值为：', round(lift, 6))
            ruleList.append((freqSet - conseq, conseq, conf))
 
# 生成规则
def gen_rule(L, supportData, minConf = 0.7):
    bigRuleList = []
    for i in range(1, len(L)):  # 从二项集开始计算
        for freqSet in L[i]:  # freqSet为所有的k项集
            # 求该三项集的所有非空子集，1项集，2项集，直到k-1项集，用H1表示，为list类型,里面为frozenset类型，
            H1 = list(freqSet)
            all_subset = []
            getSubset(H1, all_subset)  # 生成所有的子集
            calcConf(freqSet, all_subset, supportData, bigRuleList, minConf)
    return bigRuleList
 
if __name__ == '__main__':
    dataSet = data_translation
    L, supportData = apriori(dataSet, minSupport = 0.02)
    rule = gen_rule(L, supportData, minConf = 0.35)

2. 模型分析

根据多次试验，得出了26个关联规则。根据规则结果，可整理出购物篮关联规则模型结果。

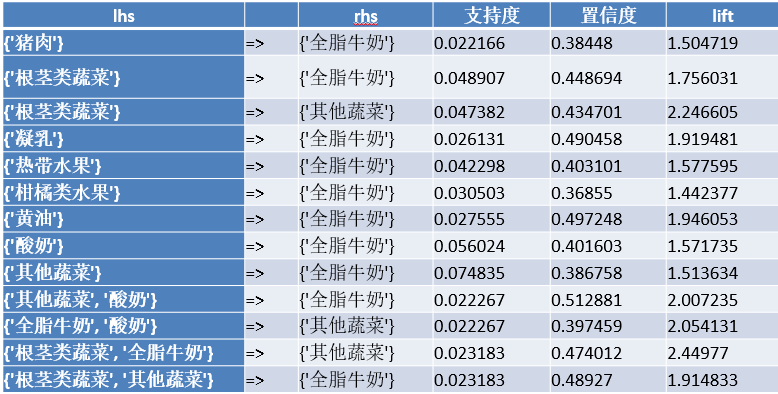
输出结果分析，顾客购买酸奶和其他蔬菜的时候会同时购买全脂牛奶，其置信度最大达到51,29%。其他蔬菜、根茎类蔬菜和全脂牛奶同时购买的概率较高。

从购物者角度进行分析：现代生活中，大多数购物者为家庭煮妇，购买的商品大部分是食品，随着生活质量和健康意识的增加，其他蔬菜、根茎类蔬菜和全脂牛奶均为现代家庭每日饮食所需品，因此，其他蔬菜、根茎类蔬菜和全脂牛奶同时购买的概率较高符合现代人们的生活健康意识。

3. 模型应用

模型结果表明顾客购买商品的时候会同时购买全脂牛奶。因此，商场应该根据实际情况将全脂牛奶放在顾客购买商品的必经之路，或者商场显眼位置，方便顾客拿取。其他蔬菜、根茎类蔬菜、酸奶油、猪肉、黄油、本地蛋类和多种水果同时购买的概率较高，可以考虑捆绑销售，或者适当调整商场布置，将这些商品的距离尽量拉近，提升购物体验。