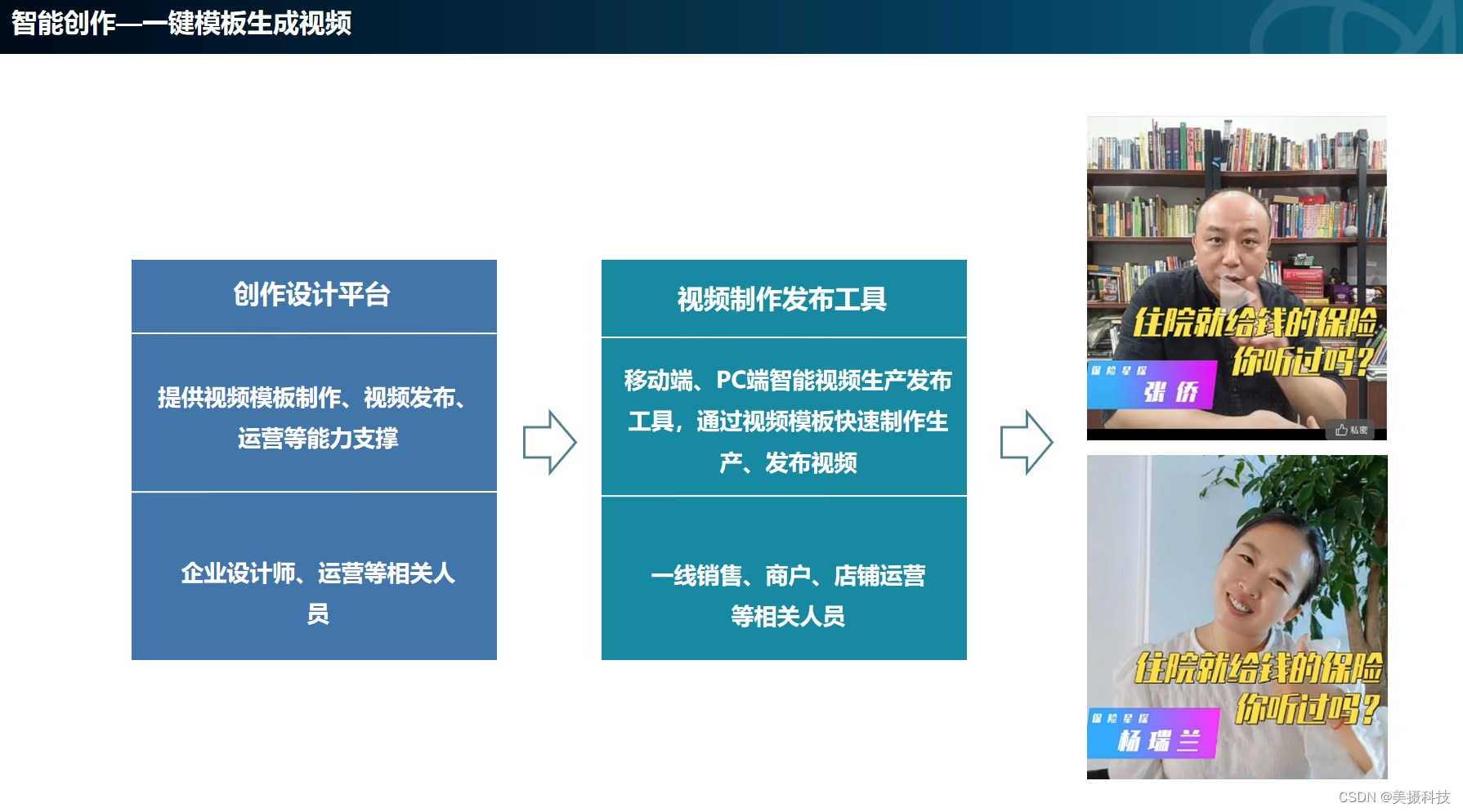
视频已经成为企业营销、宣传、培训的重要手段，高昂的制作成本、复杂的技术门槛以及繁琐的制作流程，往往让许多企业望而却步。美摄科技凭借其深厚的技术积累和创新能力，推出了面向企业的智能一键模板生成视频解决方案，为企业视频制作带来了革命性的变革。

一、高效便捷，一键生成

美摄科技的智能一键模板生成视频解决方案，采用先进的人工智能技术，结合丰富的视频模板库，为企业提供了一种全新的视频制作方式。企业只需选择适合自身需求的模板，上传相关素材，通过简单的操作，即可一键生成高质量的视频作品。这一解决方案极大地简化了视频制作的流程，提高了制作效率，让企业轻松拥有专业级的视频作品。

二、海量模板，满足多样需求

美摄科技的视频模板库涵盖了企业营销、产品宣传、员工培训等多个领域，包括开场动画、产品展示、企业文化等多种类型。企业可以根据自己的需求选择合适的模板，轻松制作出符合自身品牌风格和宣传目标的视频作品。此外，美摄科技还不断更新和优化模板库，以满足企业不断变化的需求。

三、智能剪辑，专业效果

美摄科技的智能剪辑技术，能够自动识别素材中的关键信息，进行智能剪辑和拼接，生成连贯、流畅的视频作品。同时，美摄科技还提供了丰富的特效、滤镜和字幕等编辑功能，让企业可以轻松制作出具有专业感的视频作品。这一技术不仅提高了视频制作的质量，还降低了对专业人员的依赖程度，让视频制作更加普及化。

四、数据安全，保障无忧

美摄科技高度重视数据安全，采用先进的加密技术和安全措施，确保客户数据的安全性和隐私性。在视频制作过程中，客户的素材和数据将得到严格的保护，不会被泄露或滥用。此外，美摄科技还提供了完善的客户服务和技术支持体系，确保客户在使用过程中的顺畅体验。

五、广泛应用，助力企业腾飞

美摄科技的智能一键模板生成视频解决方案已经广泛应用于各行各业的企业中，取得了显著的效果。通过这一解决方案，企业可以快速制作出符合自身需求的视频作品，提高品牌知名度和影响力；同时，还可以利用视频进行产品展示、员工培训等多元化应用，推动企业的快速发展。

美摄科技的智能一键模板生成视频解决方案以其高效便捷、海量模板、智能剪辑、数据安全和广泛应用等特点，为企业视频制作带来了全新的体验和价值。在未来，美摄科技将继续秉承创新、专业、高效的服务理念，为企业提供更多优质、高效的视频制作解决方案，助力企业在数字化时代腾飞！