布隆过滤器详解

布隆过滤器(Bloom Filter)是一种空间效率非常高的随机数据结构,由布隆(Burton Howard Bloom)在1970年提出,用于检验一个元素是否属于一个集合。
具体来说,它可能会错误地认为一个不存在的元素存在(假阳性),但绝不会把一个存在的元素误判为不存在(假阴性),文章后面会详细说明。
布隆过滤器的基本原理
布隆过滤器由一个位数组(bit array)和多个哈希函数组成:
- 位数组:一个固定长度的位数组(bit array),所有位初始化为0。
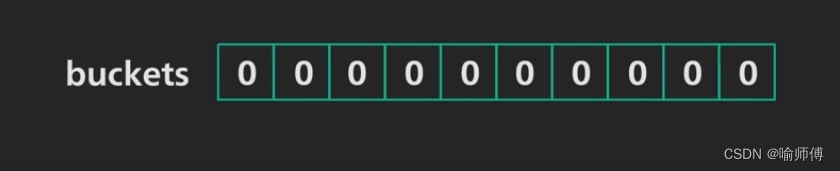
- 哈希函数:一组独立的哈希函数,每个函数将输入映射到位数组中的某个位置。
插入操作
当插入一个元素时,布隆过滤器将该元素通过k个哈希函数计算出k个位置,并将这些位置上的位设置为1。
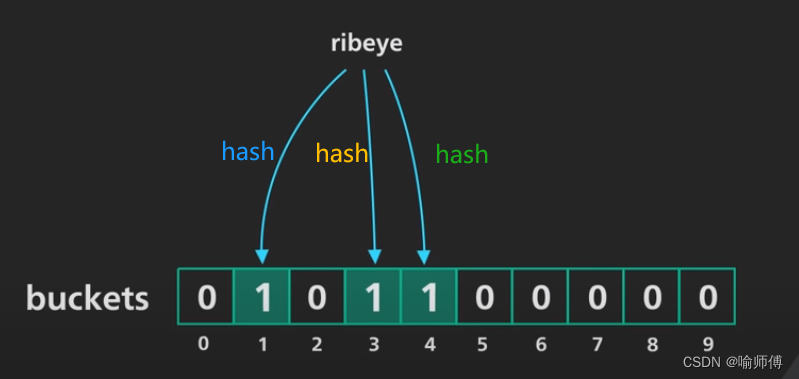
例如,假设有三个哈希函数 ( h1, h2, h3 ),插入一个元素 ( x ) 时,将位数组的 ( h1(x), h2(x), h3(x) ) 位置设置为1。

查询操作
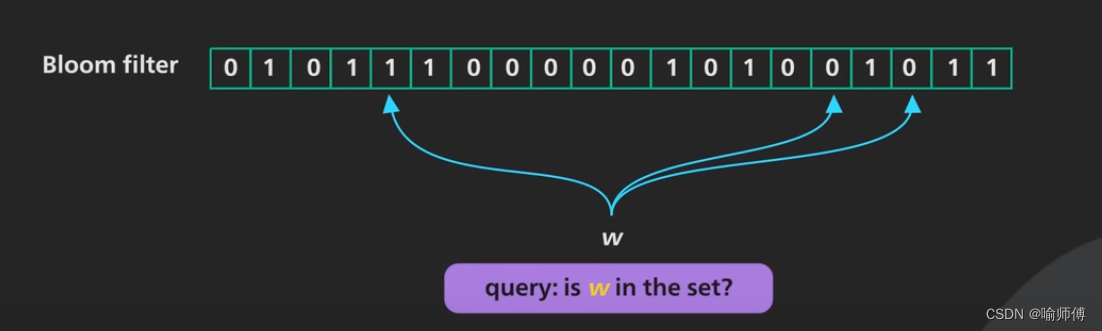
当查询一个元素是否存在时,使用同样的k个哈希函数计算出k个位置,并检查这些位置上的位是否全为1。
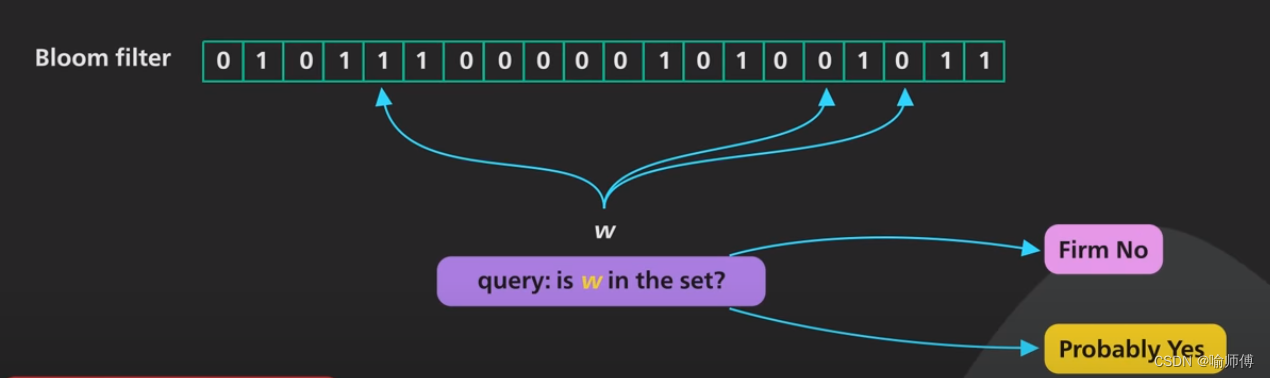
- 如果其中有一个位置为0,则该元素肯定不在(
Firm No)集合中。
- 如果所有位置都为1,则该元素可能在(
Probably Yes)集合中。
- 这里博主解释一下为什么说查询的时候结果为 “可能是”(
Probably Yes),也就是“假阳性”(False positives)。

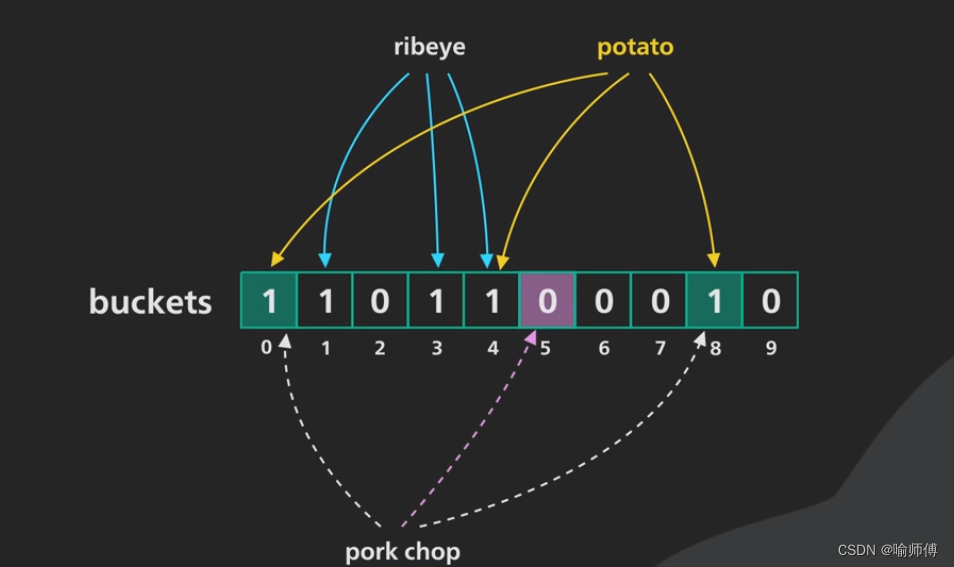
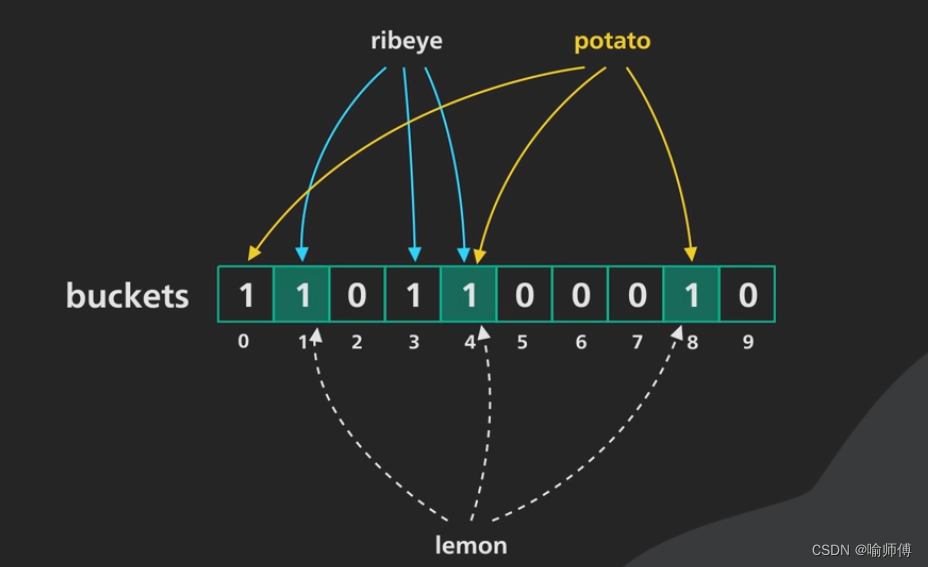
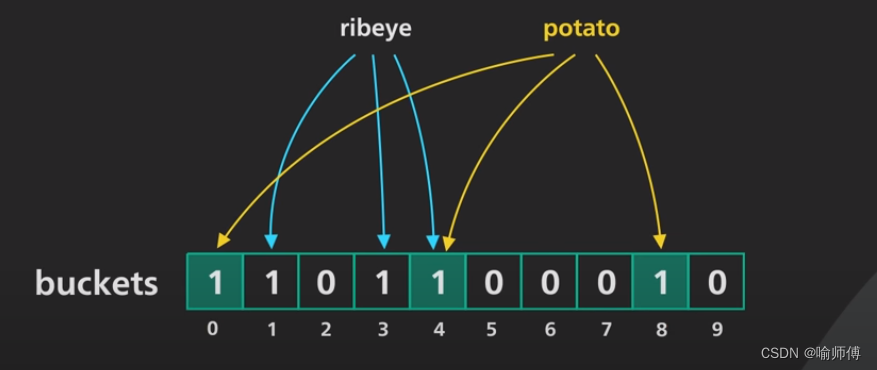
- 比如说位数组已存储的有
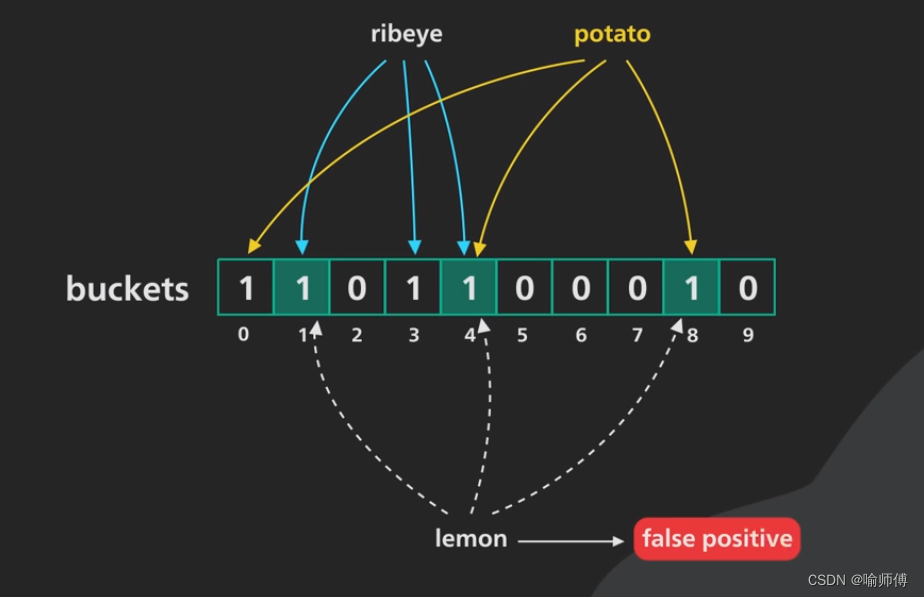
ribeye和potato两个值,这时候我们想查询lemon是否存在,于是通过哈希函数组计算哪些位上会存在1。 - 但在哈希函数组的计算下,不同的k可能会得到相同的v。计算并不存在的
lemon却得到了已存在的potato的值,也就是说我们得到的判断是——不存在位数组中的元素 存在!(假阳性出现啦!)
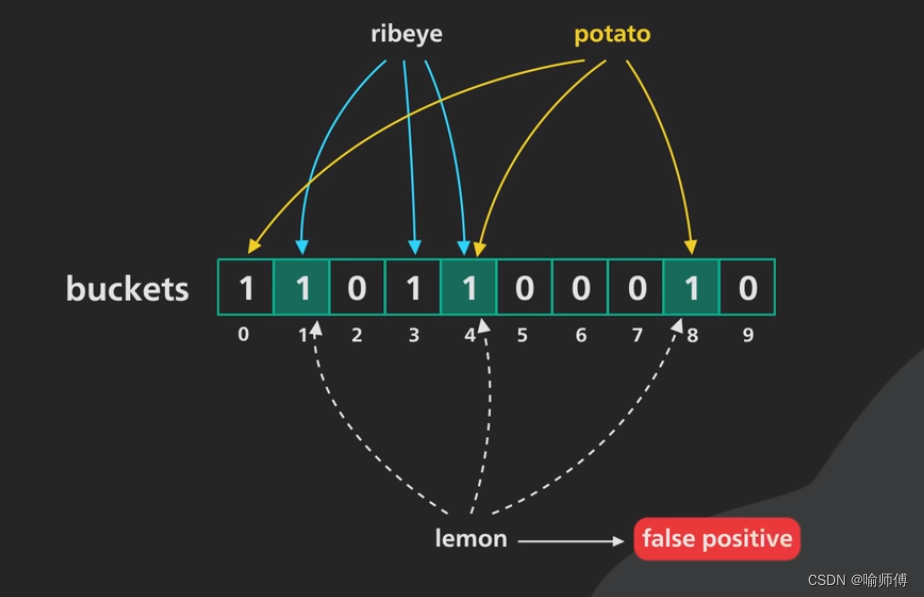
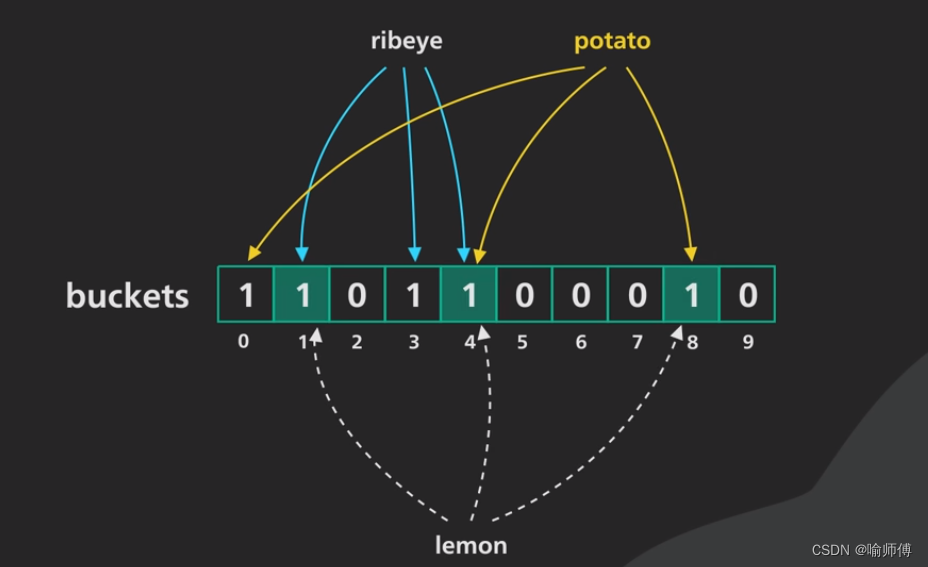
- 但是布隆过滤器肯定不会存在假阴性滴!布隆过滤器有误判率,但不会漏报。只要存在,必然会存进位数组,必然能查询到!

布隆过滤器的特点总结
1. 空间效率高
-
布隆过滤器使用一个位数组来表示集合,而不是存储实际的元素。位数组中的每一位只有两种状态:0或1。
-
通过哈希函数将元素映射到位数组的位置,以避免存储实际的元素,从而大大减少了存储空间的需求。

- 多个元素可以共享相同的位,这进一步提高了空间利用率。虽然这会带来假阳性问题,但总体上节省了大量的内存。
2. 查询速度快
- 查询操作只需要进行几次哈希运算和位数组访问。这些操作的时间复杂度是 (O(k)),其中 (k) 是哈希函数的数量。
- 在现代计算机架构中,哈希运算和数组访问都非常快速,因此查询操作可以在常数时间内完成。
3. 插入速度快
-
插入操作与查询操作类似,也是先通过 (k) 个哈希函数计算出 (k) 个位置,然后将这些位置的位设置为1。
-
由于只涉及位数组的更新和简单的哈希计算,插入操作的时间复杂度也是 (O(k)),且非常高效。
4. 无法删除元素
- 标准布隆过滤器无法删除元素,因为无法确定某个位是由哪个具体元素设置的。(假阳性)
- 由于多个元素可能导致同一个位被设置成1,删除一个元素可能会误删除其他元素的标志位,从而破坏整个过滤器的准确性。
5. 假阳性存在
-
当插入的元素数量增加时,位数组中的1的比例也会增加。这意味着不同元素通过哈希函数映射到同一位的概率增大。
-
当查询一个不存在的元素时,如果该元素的所有哈希位置都被置为1(由于其他元素的影响),布隆过滤器将返回“可能存在”,即一个假阳性。

-
假阳性率与位数组长度 (m)、哈希函数数量 (k) 和元素数量 (n) 有关。通过选择这些参数,可以控制假阳性率,但无法完全消除。
-
位数组长度 (m):
- 增大 (m):随着位数组长度的增加,每个哈希位置被设置为1的概率减小,从而降低假阳性率。
- 减小 (m):如果位数组太短,则不同元素的哈希位置更容易重叠,导致更多的位被设置为1,增加假阳性率。
-
哈希函数数量 (k):
- 优化 (k):假阳性率与哈希函数数量存在一个最优点。当 (k) 过小或过大时,假阳性率都会增加。
- 过多的哈希函数:增加哈希函数数量会增加每个元素的哈希位置数目,但也会因为重复设置同一位而降效率。
- 过少的哈希函数:减少哈希函数数量会降低每个元素的哈希位置数目,增加假阳性率。
-
元素数量 (n):
- 增大 (n):随着插入元素数量的增加,位数组中更多的位会被设置为1,导致假阳性率上升。
- 减小 (n):较少的元素数量意味着位数组中更多的位将保持为0,降低假阳性率。
布隆适用场景
布隆过滤器适合于那些可以容忍一定误判率的应用场景,但不适合需要百分百准确判断的场景。
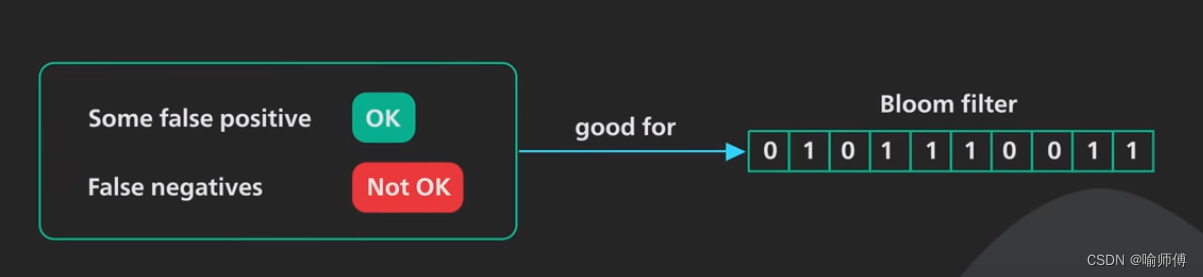
主要用于快速判断元素是否可能存在于一个庞大的集合中,如缓存、垃圾邮件过滤、网页爬虫的URL去重等
1.减少对不存在键的磁盘读取
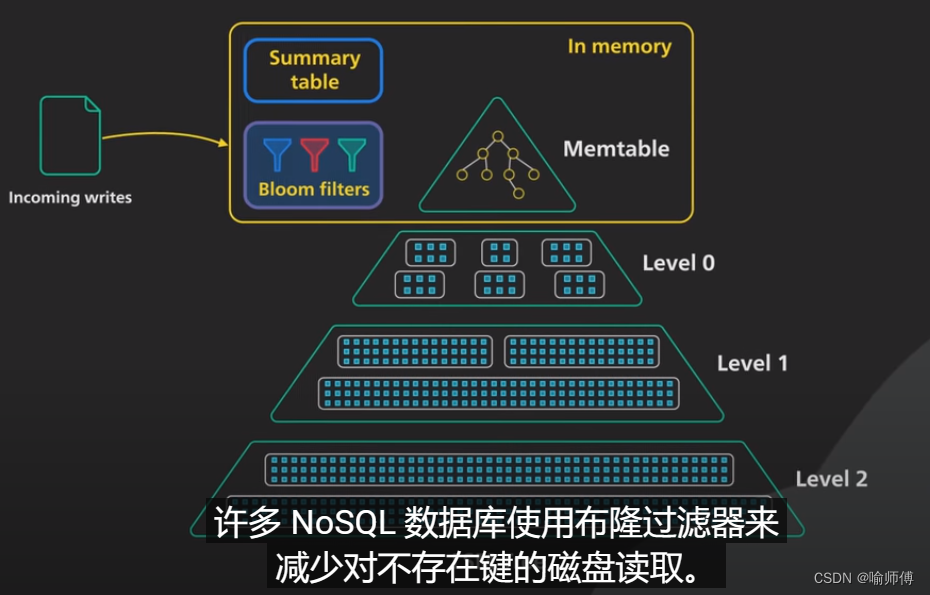
2.减少缓存工作量,提高缓存命中率。

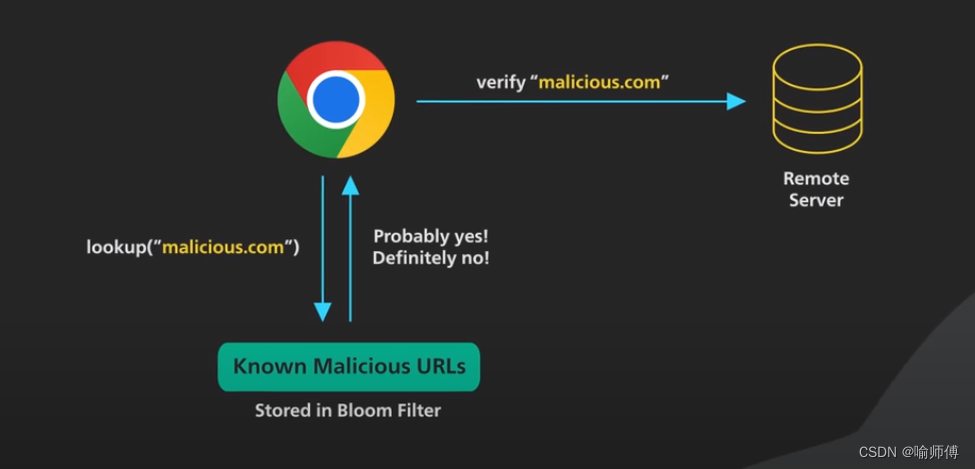
3.识别恶意网址
4.防止用户使用弱密码