问题:1058 - 求出100至999范围内的所有水仙花数。

类型：简单循环

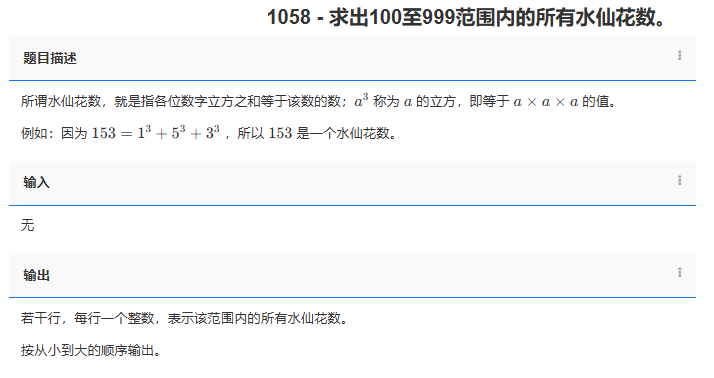
题目描述：

所谓水仙花数，就是指各位数字立方之和等于该数的数；a^3 称为 a 的立方，即等于 a×a×a 的值。
例如：因为 153=1³⁺⁵3+3^3 ，所以 153 是一个水仙花数。

输入：

无

输出：

若干行，每行一个整数，表示该范围内的所有水仙花数。

按从小到大的顺序输出。

完整代码如下：

#include<iostream>
#include<iomanip>
using namespace std;
int main(){
	
	//一、分析问题
	//已知：
	//未知：
	//关系：
	
	
	//二、数据定义 
	int a,b,c,i=100;
	//三、数据输入 
	//四、数据计算 
	for(int i=100;i<=999;i++){
		a=i%10;
		b=i/10%10;
		c=i/100%10;
		if(a*a*a+b*b*b+c*c*c==i){
			cout<<i<<endl;
		}
	}

	//五、输出结果 
	return 0;		
}