目录

一、研究问题

二、C++代码

三、计算结果

---

一、研究问题

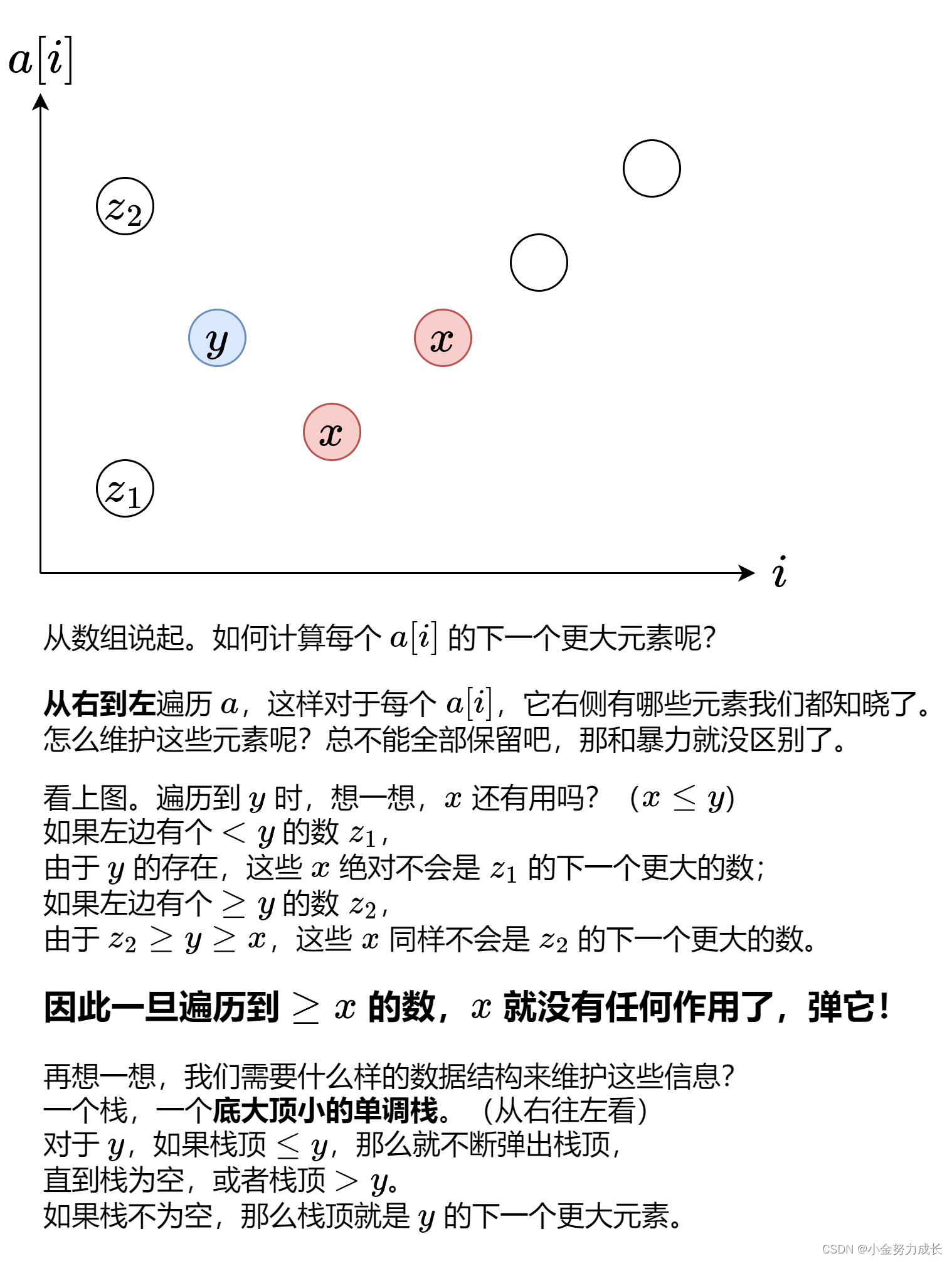
        本节我们采用梯形法（即隐式Eluer法）求解算例。

        梯形法的原理及推导请参考：

常微分方程算法之梯形法（隐式Eluer法）_梯形法求解常微分方程-CSDN博客https://blog.csdn.net/L_peanut/article/details/137273933

        研究问题依然为

取步长为0.1。

二、C++代码

---

#include <cmath>
#include <stdlib.h>
#include <stdio.h>


int main(int argc, char *argv[])
{
        int i,k,N;
        double a,b,h,y0,temp1,temp2,epsilon,err,maxerr;
        double *x,*y;
        double f(double x, double y);
        double exact(double x);

        a=0.0;  //求解区域左端点
        b=1.0;  //求解区域右端点
        N=10;   //总剖分数
        h=(b-a)/N;  //步长

        x=(double *)malloc(sizeof(double)*(N+1));   //动态分配长度为(N+1)的数组，存放节点坐标
        y=(double *)malloc(sizeof(double)*(N+1));   //动态分配长度为(N+1)的数组，存放对应节点
的数值解
        for(i=0;i<=N;i++)
                x[i]=a+i*h;   //节点坐标
        y0=1.0;
        y[0]=y0;   //初值
        maxerr=0.0;
        epsilon=1e-4;

        for(i=0;i<N;i++)
        {
                temp1=y[i]+h*f(x[i],y[i]);
                k=0;
                do
                {
                        k=k+1;
                        if(k!=1)
                                temp1=temp2;
                        temp2=y[i]+h*(f(x[i],y[i])+f(x[i+1],temp1))/2.0;
                }while(fabs(temp1-temp2)>epsilon);
                y[i+1]=temp2;
                err=fabs(y[i+1]-exact(x[i+1]));   //计算节点误差
                printf("k=%d, x[%d]=%.4f, y[%d]=%f, exact=%f, err=%f.\n",k,i+1,x[i+1],i+1,y[i+1],exact(x[i+1]),err);   //打印节点及节点上的数值解、精确解和误差
                if(err>maxerr)
                        maxerr=err;
        }
        printf("The max error is %f.\n",maxerr);  //打印最大误差

        return 0;
}


//右端项函数
double f(double x, double y)
{
        return y-2*x/y;
}
//精确解
double exact(double x)
{
        return sqrt(1.0+2*x);
}

---

三、计算结果

k=3, x[1]=0.1000, y[1]=1.095657, exact=1.095445, err=0.000212.
k=3, x[2]=0.2000, y[2]=1.183596, exact=1.183216, err=0.000380.
k=3, x[3]=0.3000, y[3]=1.265444, exact=1.264911, err=0.000532.
k=3, x[4]=0.4000, y[4]=1.342327, exact=1.341641, err=0.000686.
k=3, x[5]=0.5000, y[5]=1.415064, exact=1.414214, err=0.000850.
k=3, x[6]=0.6000, y[6]=1.484274, exact=1.483240, err=0.001034.
k=3, x[7]=0.7000, y[7]=1.550437, exact=1.549193, err=0.001244.
k=2, x[8]=0.8000, y[8]=1.613948, exact=1.612452, err=0.001496.
k=2, x[9]=0.9000, y[9]=1.675112, exact=1.673320, err=0.001792.
k=2, x[10]=1.0000, y[10]=1.734192, exact=1.732051, err=0.002141.
The max error is 0.002141.

        同样的算例，在上一节中采用欧拉法的计算结果误差为：

x[1]=0.1000, y[1]=1.100000, exact=1.095445, err=0.004555.
x[2]=0.2000, y[2]=1.191818, exact=1.183216, err=0.008602.
x[3]=0.3000, y[3]=1.277438, exact=1.264911, err=0.012527.
x[4]=0.4000, y[4]=1.358213, exact=1.341641, err=0.016572.
x[5]=0.5000, y[5]=1.435133, exact=1.414214, err=0.020919.
x[6]=0.6000, y[6]=1.508966, exact=1.483240, err=0.025727.
x[7]=0.7000, y[7]=1.580338, exact=1.549193, err=0.031145.
x[8]=0.8000, y[8]=1.649783, exact=1.612452, err=0.037332.
x[9]=0.9000, y[9]=1.717779, exact=1.673320, err=0.044459.
x[10]=1.0000, y[10]=1.784771, exact=1.732051, err=0.052720.

        可见梯形法的计算精度明显优于欧拉法。