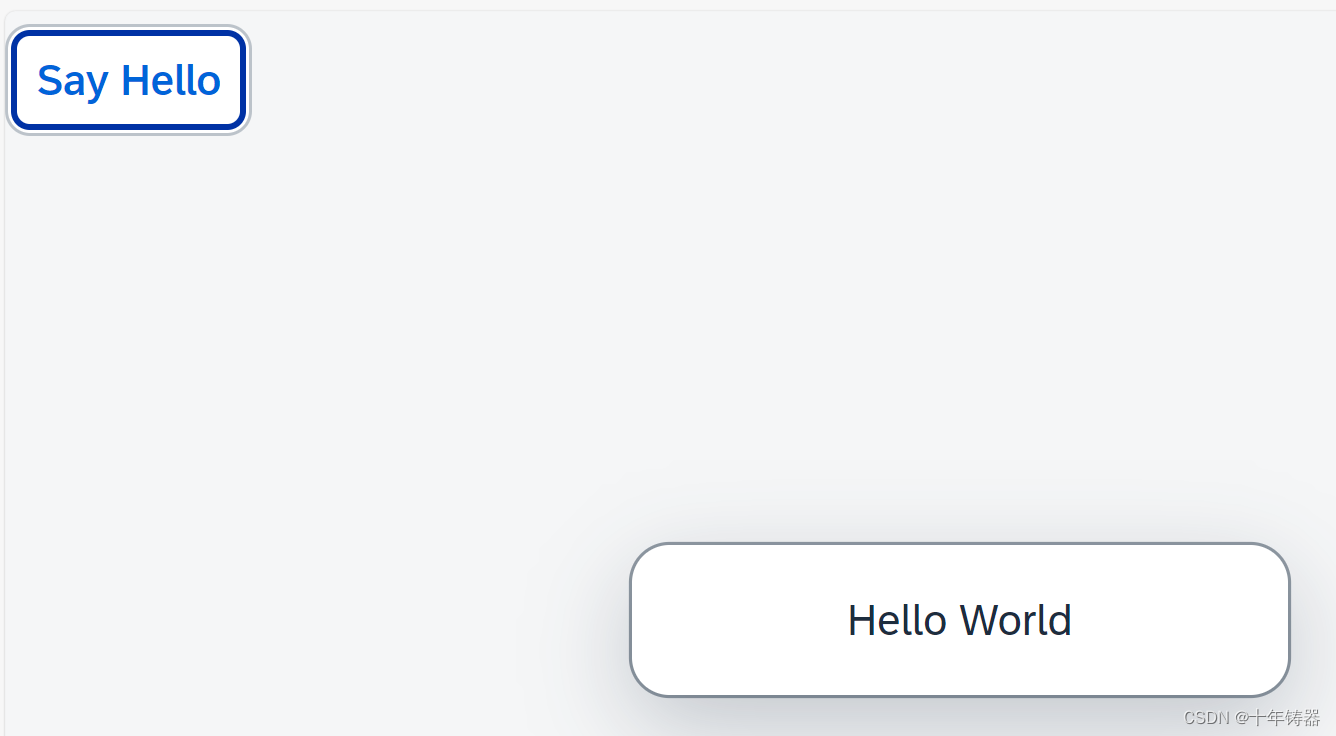
一、放缩技巧

技巧1

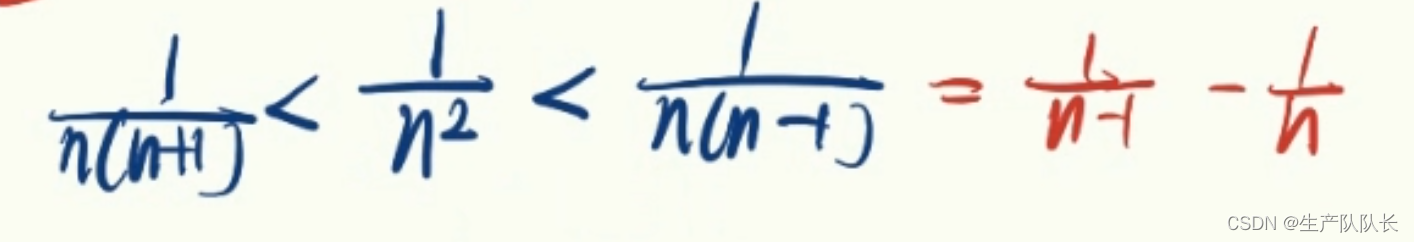
例题
证明：S_n＜1

解：

变形

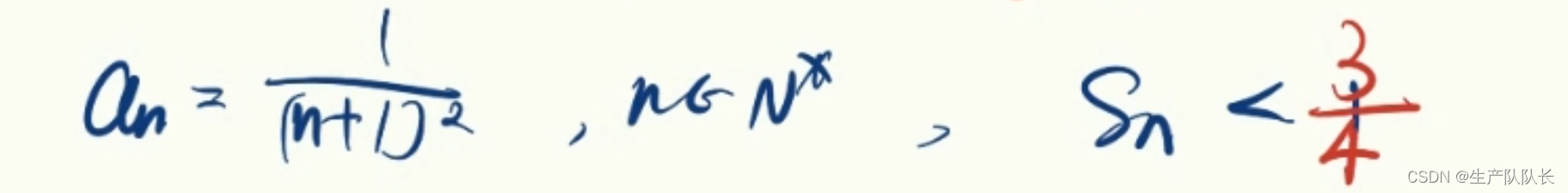
解：
由于第一种情况，我们证明了S_n＜1，n≥1，是从第一项就开始放缩的。
发现，无法精确到 $\frac{3}{4}$

这时，我们就从第二项开始放缩，最终得解。
如果第二项不行，从第三项。以此类推。最终可得解。

总结
本题，我们知道前两项和是
$$\frac{1}{4}+\frac{1}{9}=\frac{13}{36}$$
那么，我们可以将题目改成
$$S_n<\frac{23}{36}$$
这个时候，放缩，就要从第三项开始放缩。

技巧2

在1的基础上，提高放缩精确度。
利用平方差公式，进行放缩。

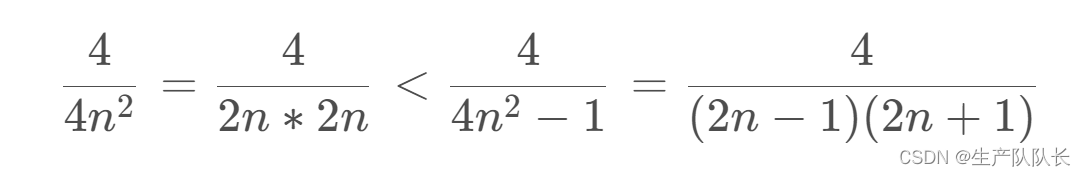
例题

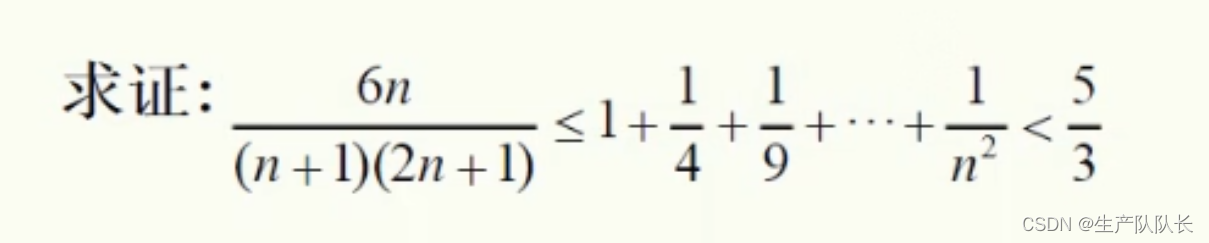
解析：
这里有两个不等号，所以，要证明两次
对于，左边的不等号，我们可以采用技巧1的方式
放缩后，结合二次函数的性质，求出单调性发范围，从而得证
而对于，右边的不等号，我们采用技巧1，就不行了。
分析原因
技巧1中
$$n^2>n\ast (n-1)=n^2-n，可以看出，误差是一个n。$$
那么，我们如何放缩了？
这里含有一个$n^2$，所以，我们可以想到平方差公式，写成两项乘积的形式
从而，可以使用裂项求和法。
可以这样放缩
$$\frac{4}{4n^2}=\frac{4}{2n\ast 2n}<\frac{4}{4n^2-1}=\frac{4}{(2n-1)(2n+1)}$$
或者
$$\frac{1}{n^2}<\frac{1}{n^2-1}=\frac{1}{(n-1)(n+1)}$$
这两种放缩方式，都可以解决第二个不等号
放缩技巧都是利用平方差公式
放缩原则：减小误差范围。单项，从误差为n，降到误差为常数C

左边不等号

右边不等号

换放缩方案

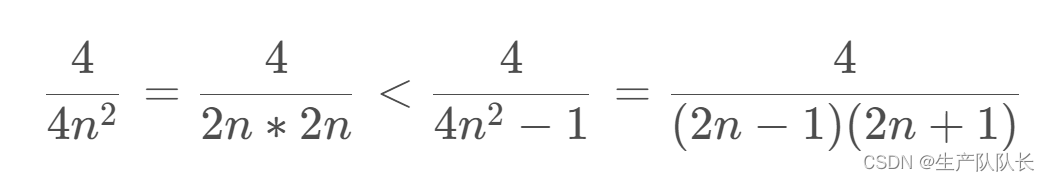
从第二项开始放缩：

总结
上面，我们试了4中放缩方式，现在来说明一下他们之间的精确度
比较他们的大小关系如下：
$$\frac{1}{n^2-n}>\frac{1}{n^2-1}>\frac{4}{4n^2-1}>\frac{1}{n^2}$$
可以发现
$$\frac{4}{4n^2-1}$$
距离
$$\frac{1}{n^2}$$
更近，所以，这个放缩更精确。
以此类推

二、数列不等式放缩原则

1、提高放缩通项公式的精确度。
2、从后几项开始放缩。