PPT 截取有用信息。 课程网站做习题。总体 MOOC 过一遍
- 1、学堂在线 视频 + 习题
- 2、相应章节 过电子书 复习 GitHub界面链接
- 3、总体 MOOC 过一遍
- 还是跳过了一些 P38
学堂在线 课程页面链接
中国大学MOOC 课程页面链接
B 站 视频链接
PPT和书籍下载网址: 【github链接】
文章目录
- 2.1 return:可评估策略的好坏
- 计算 return
- 方法一: 根据定义
- 方法二: 根据状态间 回报 的依赖关系
- 2.3 State value 状态值 v π ( s ) v_\pi(s) vπ(s)
- 2.4 贝尔曼公式 推导
- 2.5 如何写出 Bellman 方程并逐步计算状态值
- 2.6 贝尔曼公式的 矩阵 和 向量 形式
- 2.7 求解 贝尔曼公式 —> 求得 状态值
- 2.8 Action value 动作值 q π ( s , a ) q_\pi(s, a) qπ(s,a)
状态值:agent 在遵循给定策略时所能获得的平均奖励。
状态值越大,对应的策略越好。
状态值可以用作 评估策略是否良好 的度量。
通过求解 Bellman 方程,可以得到状态值。

状态值
贝尔曼公式

——————
2.1 return:可评估策略的好坏
回报 return:沿着 一个轨迹 获得的 奖励 折扣和。
可用于 评估策略
return 可以评估策略的好坏
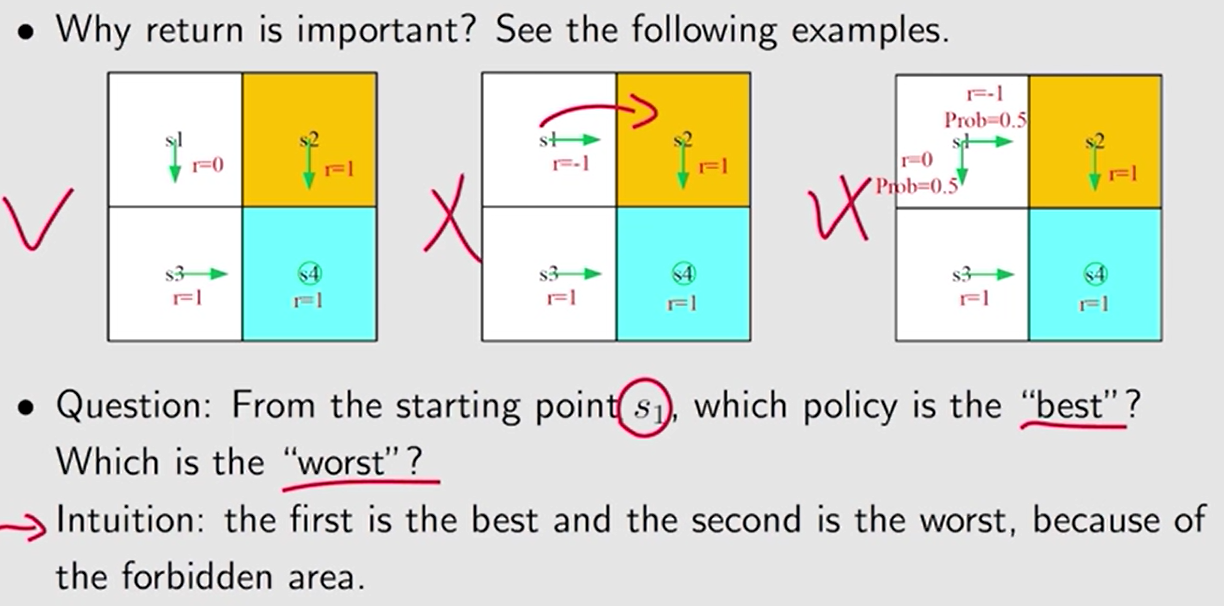
计算 return 的值,来评估以下 3 个策略
3 种策略的区别在于第一格。 策略 1 是往下走,策略 2 是 往右走,策略 3 往下 和 往右的概率 分别为 50%。其它格相同。
计算 return
方法一: 根据定义
回报 return 等于沿轨迹收集的所有奖励的折扣总和。
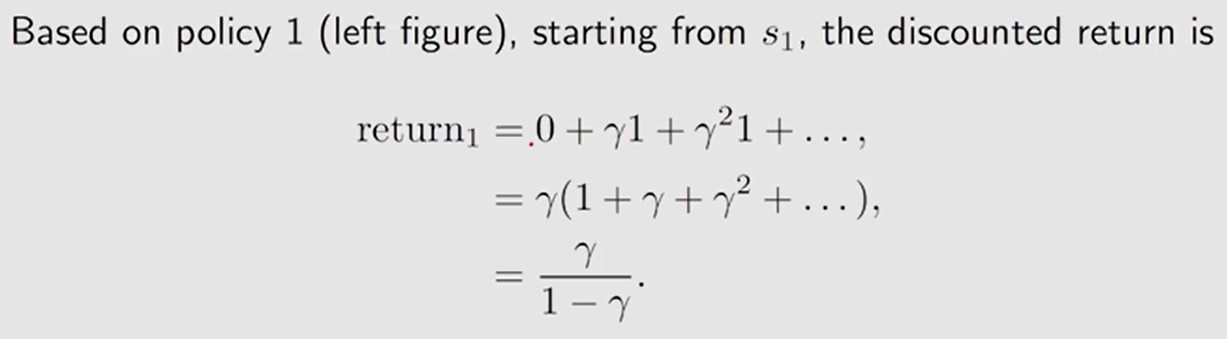


r e t u r n 3 \rm return_3 return3 严格来说是 状态值。【计算涉及两条轨迹】 从状态 s 1 s_1 s1 出发得到的平均 return。
return 是针对 一个 轨迹 而言。
状态值 可能是 多个轨迹。

通过数学求解得到的结论和直觉一致, 成功将直觉数学化。
——> 可用 return 评估策略。
方法二: 根据状态间 回报 的依赖关系
v i v_i vi: 从 s i s_i si 出发获得的回报
例:

推导:
v 1 = r 1 + γ r 2 + γ 2 r 3 + . . . = r 1 + γ ( r 2 + γ r 3 + . . . ) = r 1 + γ v 2 v_1=r_1+\gamma r_2 + {\gamma}^2r_3+...=r_1 +\gamma(r_2+\gamma r_3+...)=r_1+\gamma v_2 v1=r1+γr2+γ2r3+...=r1+γ(r2+γr3+...)=r1+γv2
v 2 = r 2 + γ r 3 + γ 2 r 4 + . . . = r 2 + γ ( r 3 + γ r 4 + . . . ) = r 2 + γ v 3 v_2=r_2+\gamma r_3 + {\gamma}^2r_4+...=r_2 +\gamma(r_3+\gamma r_4+...)=r_2+\gamma v_3 v2=r2+γr3+γ2r4+...=r2+γ(r3+γr4+...)=r2+γv3
v 3 = r 3 + γ r 4 + γ 2 r 1 + . . . = r 3 + γ ( r 4 + γ r 1 + . . . ) = r 3 + γ v 4 v_3=r_3+\gamma r_4 + {\gamma}^2r_1+...=r_3 +\gamma(r_4+\gamma r_1+...)=r_3+\gamma v_4 v3=r3+γr4+γ2r1+...=r3+γ(r4+γr1+...)=r3+γv4
v 4 = r 4 + γ r 1 + γ 2 r 2 + . . . = r 4 + γ ( r 1 + γ r 2 + . . . ) = r 4 + γ v 1 v_4=r_4+\gamma r_1 + {\gamma}^2r_2+...=r_4 +\gamma(r_1+\gamma r_2+...)=r_4+\gamma v_1 v4=r4+γr1+γ2r2+...=r4+γ(r1+γr2+...)=r4+γv1
~
写成矩阵形式[ v 1 v 2 v 3 v 4 ] = [ r 1 r 2 r 3 r 4 ] + γ [ v 2 v 3 v 4 v 1 ] = [ r 1 r 2 r 3 r 4 ] + γ [ 0 1 0 0 0 0 1 0 0 0 0 1 1 0 0 0 ] [ v 1 v 2 v 3 v 4 ] v = r + γ P v \begin{align*} \begin{bmatrix} v_1 \\ v_2 \\ v_3 \\ v_4 \\ \end{bmatrix} &= \begin{bmatrix} r_1 \\ r_2 \\ r_3 \\ r_4 \\ \end{bmatrix} + \gamma\begin{bmatrix} v_2 \\ v_3 \\ v_4 \\ v_1 \end{bmatrix}\\ ~\\ &= \begin{bmatrix} r_1 \\ r_2 \\ r_3 \\ r_4 \\ \end{bmatrix} + \gamma\begin{bmatrix} 0 & 1 & 0 & 0\\ 0 & 0 & 1 & 0\\ 0 & 0 & 0 & 1\\ 1 & 0 & 0 & 0 \end{bmatrix}\begin{bmatrix} v_1\\ v_2 \\ v_3 \\ v_4 \\ \end{bmatrix}\\ ~\\\mathbf{v}&=\mathbf{r}+\gamma\mathbf{P}\mathbf{v} \end{align*} v1v2v3v4 v= r1r2r3r4 +γ v2v3v4v1 = r1r2r3r4 +γ 0001100001000010 v1v2v3v4 =r+γPv
Bellman 方程的核心思想:从一种状态出发所获得的收益依赖于从其他状态出发所获得的收益。
从不同状态出发得到的 return , 依赖于 从其它状态 出发得到的 return。【强化学习中的 Bootstrapping 思想】
Bootstrapping:从自己出发不断迭代得到的一些结果。

2.3 State value 状态值 v π ( s ) v_\pi(s) vπ(s)
之前提到, 回报 return 可用来评估策略。然而,它们不适用于随机系统,因为从一个状态出发可能导致不同的回报。
——> 用 状态值 评估

随机变量 大写
多步 trajectory:
S
t
→
A
t
R
t
+
1
,
S
t
+
1
→
A
t
+
1
R
t
+
2
,
S
t
+
2
→
A
t
+
2
R
t
+
3
,
⋯
S_t\xrightarrow{A_t}R_{t+1},S_{t+1}\xrightarrow{A_{t+1}}R_{t+2},S_{t+2}\xrightarrow{A_{t+2}}R_{t+3},\cdots
StAtRt+1,St+1At+1Rt+2,St+2At+2Rt+3,⋯
折扣回报:
G
t
=
R
t
+
1
+
γ
R
t
+
2
+
γ
2
R
t
+
3
+
⋯
G_t=R_{t+1}+\gamma R_{t+2}+{\gamma}^2R_{t+3}+\cdots
Gt=Rt+1+γRt+2+γ2Rt+3+⋯
- γ ∈ [ 0 , 1 ) \gamma \in [0, 1) γ∈[0,1) 为折扣率
R t + 1 R_{t+1} Rt+1 开始累积 !!!
——————————————
状态值函数 / 状态值:
v
π
(
s
)
=
E
[
G
t
∣
S
t
=
s
]
v_\pi(s)=\mathbb{E}[G_t|S_t=s]
vπ(s)=E[Gt∣St=s]
- G t G_t Gt 的期望【期望值/均值】
- 状态值的值还具有价值的含义, 值越大, 表示价值越大,从这个状态出发能获得更多的回报。
状态值 v π ( s ) v_\pi(s) vπ(s) 取决于 状态 s s s 和 策略 π \pi π, 和 时间步长 t t t 无关。
return VS state value
return: 针对 单个 trajectory
state value: 多个 trajectory 的 return 的平均值
- 从 某个状态 出发,有可能得到多个 trajectory,此时得到的值可能不一样。
- 当 从 某个状态出发,仅存在一条 trajectory,此时两者相同
状态值与回报 return 之间的关系:
- 当策略和系统模型都是确定的时,从一个状态出发总是会导致相同的轨迹。在这种情况下,从一个状态开始获得的回报值等于状态值。
- 当策略或系统模型是随机的,从相同的状态出发可能会产生不同的轨迹。在这种情况下,不同轨迹的回报是不同的,状态值是这些回报的均值。
虽然可以使用 回报 return 来评估策略,如 2.1 节所示,但是使用状态值来评估策略更为正式:状态值更大的策略更好。
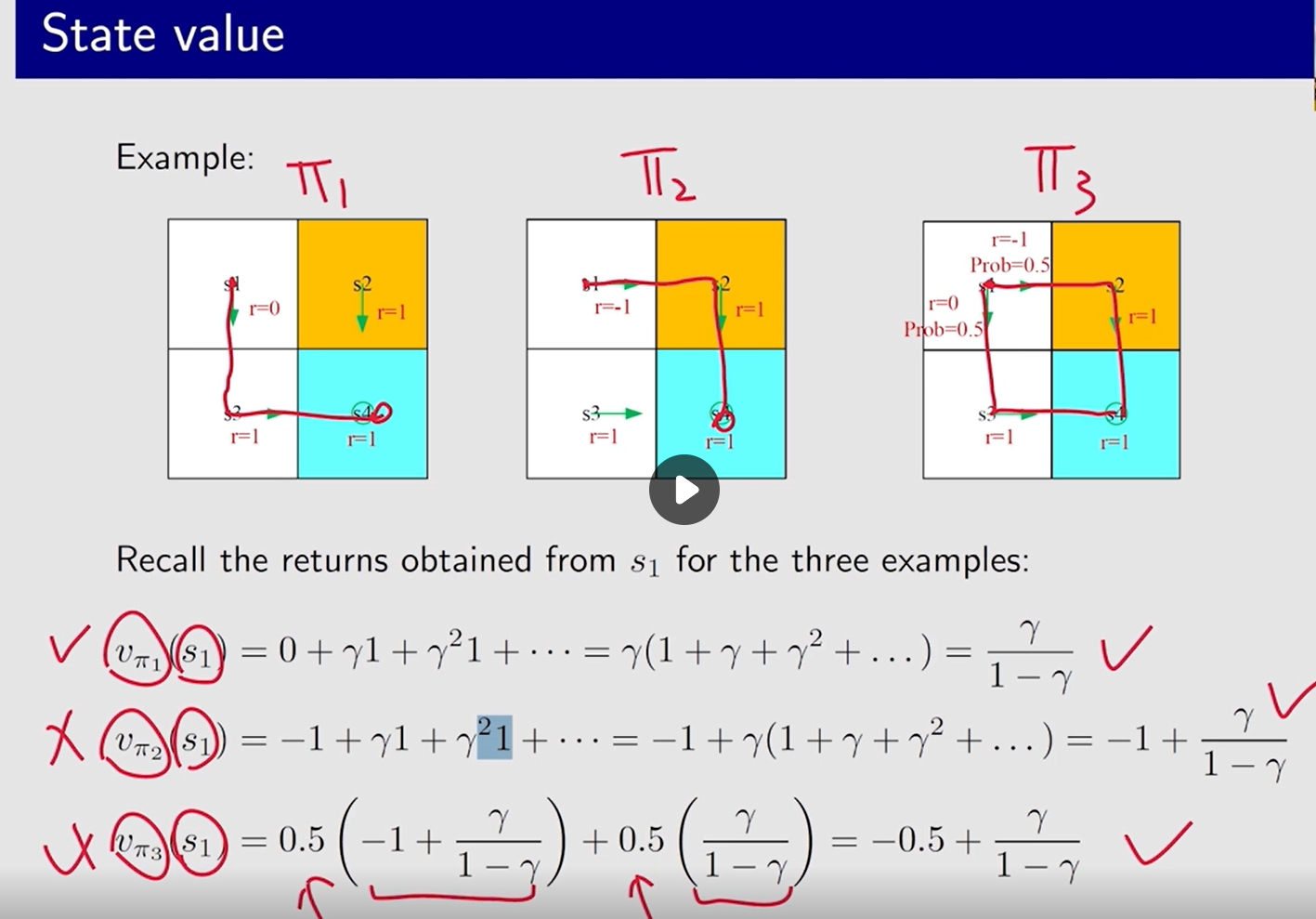
计算 3 个不同策略下, 同一状态 s 1 s_1 s1 出发 的 value
2.4 贝尔曼公式 推导
P3 贝尔曼公式 推导
贝尔曼公式 描述了 不同状态 的 state value 之间的关系。
对于某个 trajectory:
S t → A t R t + 1 , S t + 1 → A t + 1 R t + 2 , S t + 2 → A t + 2 R t + 3 , . . . S_t\xrightarrow{A_t}R_{t+1},S_{t+1}\xrightarrow{A_{t+1}}R_{t+2},S_{t+2}\xrightarrow{A_{t+2}}R_{t+3},... StAtRt+1,St+1At+1Rt+2,St+2At+2Rt+3,...
折扣回报:
G t = R t + 1 + γ R t + 2 + γ 2 R t + 3 + . . . = R t + 1 + γ ( R t + 2 + γ R t + 3 + . . . ) = R t + 1 + γ G t + 1 \begin{align*}G_t &=R_{t+1}+\gamma R_{t+2}+{\gamma}^2R_{t+3}+...\\ &= R_{t+1}+\gamma (R_{t+2}+\gamma R_{t+3}+...)\\ &=R_{t+1}+\gamma G_{t+1}\end{align*} Gt=Rt+1+γRt+2+γ2Rt+3+...=Rt+1+γ(Rt+2+γRt+3+...)=Rt+1+γGt+1
状态值
v π ( s ) = E [ G t ∣ S t = s ] = E [ R t + 1 + γ G t + 1 ∣ S t = s ] = E [ R t + 1 ∣ S t = s ] + γ E [ G t + 1 ∣ S t = s ] \begin{align*}v_\pi(s)&=\mathbb{E}[G_t|S_t=s] \\ &=\mathbb{E}[R_{t+1}+\gamma G_{t+1}|S_t=s]\\ &=\mathbb{E}[R_{t+1}|S_t=s]+\gamma \mathbb{E}[G_{t+1}|S_t=s]\end{align*} vπ(s)=E[Gt∣St=s]=E[Rt+1+γGt+1∣St=s]=E[Rt+1∣St=s]+γE[Gt+1∣St=s]
其中
即时奖励 均值
E [ R t + 1 ∣ S t = s ] = ∑ a π ( a ∣ s ) E [ R t + 1 ∣ S t = s , A t = a ] = ∑ a π ( a ∣ s ) ∑ r p ( r ∣ s , a ) r \begin{align*}\mathbb{E}[R_{t+1}|S_t=s] &= \sum_a\pi(a|s)\mathbb{E}[R_{t+1}|S_t=s, A_t=a]\\ &=\sum_a\pi(a|s)\sum_rp(r|s, a)r\end{align*} E[Rt+1∣St=s]=a∑π(a∣s)E[Rt+1∣St=s,At=a]=a∑π(a∣s)r∑p(r∣s,a)r
- 动作的集和 A ( s ) , a ∈ A ( s ) \textcolor{blue}{\mathcal A(s)}, a \in \mathcal A(s) A(s),a∈A(s);回报的集合 R ( s , a ) , r ∈ R ( s , a ) \textcolor{blue}{\mathcal R(s, a)},r\in\mathcal R(s, a) R(s,a),r∈R(s,a)
~
在状态 s s s,可以执行多个动作,执行 动作 a a a 的概率是 π ( a ∣ s ) \pi(a|s) π(a∣s), 得到的回报是后面那一串 【从 s s s 出发, 执行动作 a a a, 得到奖励 r r r 的概率是 p ( r ∣ s , a ) p(r|s, a) p(r∣s,a), 分别乘上奖励 r r r 的值,求和得到期望】。
~
未来奖励 【延迟奖励】均值
E [ G t + 1 ∣ S t = s ] = ∑ s ′ E [ G t + 1 ∣ S t = s , S t + 1 = s ′ ] p ( s ′ ∣ s ) = ∑ s ′ E [ G t + 1 ∣ S t + 1 = s ′ ] p ( s ′ ∣ s ) 马尔可夫性质:仅取决于当前的状态,和之前的状态无关 = ∑ s ′ v π ( s ′ ) p ( s ′ ∣ s ) = ∑ s ′ v π ( s ′ ) ∑ a p ( s ′ ∣ s , a ) π ( a ∣ s ) \begin{align*}\mathbb{E}[G_{t+1}|S_t=s] &= \sum_{s^{\prime}}\mathbb{E}[G_{t+1}|\textcolor{blue}{S_t=s, }S_{t+1}=s^{\prime}]p(s^{\prime}|s)\\ &=\sum_{s^{\prime}}\mathbb{E}[G_{t+1}|S_{t+1}=s^{\prime}]p(s^{\prime}|s)~~~~~\textcolor{blue}{马尔可夫性质:仅取决于当前的状态,和之前的状态无关}\\ &= \sum_{s^{\prime}} v_\pi (s^{\prime})p(s^{\prime}|s)\\ &= \sum_{s^{\prime}} v_\pi (s^{\prime})\sum_ap(s^{\prime}|s, a)\pi(a|s)\end{align*} E[Gt+1∣St=s]=s′∑E[Gt+1∣St=s,St+1=s′]p(s′∣s)=s′∑E[Gt+1∣St+1=s′]p(s′∣s) 马尔可夫性质:仅取决于当前的状态,和之前的状态无关=s′∑vπ(s′)p(s′∣s)=s′∑vπ(s′)a∑p(s′∣s,a)π(a∣s)
从状态 s s s 出发, 得到下一时刻 return 的均值
从状态 s s s 出发, 可以跳到多个不同的状态 s ′ s^\prime s′,跳到 s ′ s^\prime s′ 的概率是 p ( s ′ ∣ s ) p(s^\prime|s) p(s′∣s), 折扣和是前面那一串
表征状态值 之间关系 的 贝尔曼公式:

每个状态 有一个这样的方程。
——————————————
PDF 补充:
贝尔曼公式:
v π ( s ) = ∑ a π ( a ∣ s ) [ ∑ r p ( r ∣ s , a ) r + γ ∑ s ′ p ( s ′ ∣ s , a ) v π ( s ′ ) ] v_\pi(s)=\sum\limits_{a}\pi(a|s)\Big[\sum\limits_{r}p(r|s,a)r + \gamma \sum\limits_{s^\prime}p(s^\prime|s,a)v_\pi(s^\prime)\Big] vπ(s)=a∑π(a∣s)[r∑p(r∣s,a)r+γs′∑p(s′∣s,a)vπ(s′)]
贝尔曼公式 的 另两种等效写法:
等效 写法一:
p ( s ′ ∣ s , a ) = ∑ r p ( s ′ , r ∣ s , a ) p(s^\prime|s, a)=\sum\limits_{r}p(s^\prime,r|s, a)~~~~ p(s′∣s,a)=r∑p(s′,r∣s,a) 后续是否 进入 某个状态 取决于 回报p ( r ∣ s , a ) = ∑ s ′ p ( s ′ , r ∣ s , a ) p(r|s, a)=\sum\limits_{s^\prime}p(s^\prime,r|s, a)~~~~ p(r∣s,a)=s′∑p(s′,r∣s,a) 获得 某个回报 的概率 取决于 后续状态
v π ( s ) = ∑ a π ( a ∣ s ) ∑ s ′ ∑ r p ( s ′ , r ∣ s , a ) [ r + γ v π ( s ′ ) ] ) v_\pi(s)=\sum\limits_a\pi(a|s)\textcolor{blue}{\sum\limits_{s^\prime}\sum\limits_rp(s^\prime,r|s, a)}[r+\gamma v_\pi(s^\prime)]) vπ(s)=a∑π(a∣s)s′∑r∑p(s′,r∣s,a)[r+γvπ(s′)])
等效 写法二 : 某些问题的 回报 r r r 仅取决于 下一状态 s ′ s^\prime s′
v π ( s ) = ∑ a π ( a ∣ s ) ∑ s ′ p ( s ′ ∣ s , a ) [ r ( s ′ ) + γ v π ( s ′ ) ] v_\pi(s)=\sum\limits_a\pi(a|s)\sum\limits_{s^\prime}p(s^\prime|s,a)[r(s^\prime)+\gamma v_\pi(s^\prime)] vπ(s)=a∑π(a∣s)s′∑p(s′∣s,a)[r(s′)+γvπ(s′)]
——————————————
2.5 示例:确定 相应的贝尔曼方程
2.5 如何写出 Bellman 方程并逐步计算状态值
如何写出 Bellman 方程并逐步计算状态值。


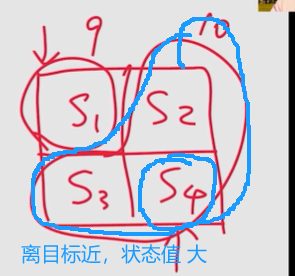
示例 2:



上一个 示例采取的策略 计算得到的
v
π
(
s
1
)
v_\pi(s_1)
vπ(s1) 比当前 这个示例 大, 因为 上一个 示例直接往下走, 当前这个示例 有 50% 的 概率 会 往 右走,有可能会进入 禁区,策略没有上一个示例的好。
状态值大 ——> 策略好。
2.6 贝尔曼公式的 矩阵 和 向量 形式
状态值
v π ( s ) = E [ R t + 1 ∣ S t = s ] + γ E [ G t + 1 ∣ S t = s ] = ∑ a π ( a ∣ s ) ∑ r p ( r ∣ s , a ) r + γ ∑ a π ( a ∣ s ) ∑ s ′ p ( s ′ ∣ s , a ) v π ( s ′ ) = r π ( s ) + γ ∑ s ′ p π ( s ′ ∣ s ) v π ( s ′ ) \begin{align*}v_\pi(s) &=\mathbb{E}[R_{t+1}|S_t=s]+\gamma \mathbb{E}[G_{t+1}|S_t=s] \\ &=\sum_a\pi(a|s)\sum_rp(r|s, a)r + \gamma\sum_a \pi(a|s)\sum_{s^{\prime}} p(s^{\prime}|s, a)v_\pi (s^{\prime})\\ &= r_\pi(s)+\gamma\sum_{s^{\prime}}p_\pi(s^{\prime}|s)v_\pi(s^{\prime})\end{align*} vπ(s)=E[Rt+1∣St=s]+γE[Gt+1∣St=s]=a∑π(a∣s)r∑p(r∣s,a)r+γa∑π(a∣s)s′∑p(s′∣s,a)vπ(s′)=rπ(s)+γs′∑pπ(s′∣s)vπ(s′)
v π ( s i ) = r π ( s i ) + γ ∑ s j p π ( s j ∣ s i ) v π ( s j ) v_\pi(s_i)=r_\pi(s_i) + \gamma\sum_{s_j}p_\pi(s_j|s_i)v_\pi(s_j) vπ(si)=rπ(si)+γsj∑pπ(sj∣si)vπ(sj)
v π = r π + γ P π v π \bm v_\pi=\bm{r}_\pi+\gamma \bm P_\pi \bm v_\pi vπ=rπ+γPπvπ
- 状态转移矩阵 P π ∈ R n × n ~P_\pi\in\mathbb R^{n\times n} Pπ∈Rn×n, [ P π ] i j = p π ( s j ∣ s i ) [P_\pi]_{ij}=p_\pi(s_j|s_i)~~~ [Pπ]ij=pπ(sj∣si) 矩阵 P π P_\pi Pπ 第 i i i 行第 j j j 列的值
- v π = [ v π ( s 1 ) , v π ( s 2 ) , ⋯ , v π ( s n ) ] T ∈ R n \bm v_\pi=[v_\pi(s_1),v_\pi(s_2), \cdots, v_\pi(s_n)]^T\in \mathbb R^n vπ=[vπ(s1),vπ(s2),⋯,vπ(sn)]T∈Rn
- r π = [ r π ( s 1 ) , r π ( s 2 ) , ⋯ , r π ( s n ) ] T ∈ R n \bm r_\pi=[r_\pi(s_1),r_\pi(s_2), \cdots,r_\pi(s_n)]^T\in \mathbb R^n rπ=[rπ(s1),rπ(s2),⋯,rπ(sn)]T∈Rn
关于 状态转移矩阵
P
π
P_\pi
Pπ:
1、非负矩阵,所有元素都等于或大于零。
P
π
≥
0
P_\pi\geq0
Pπ≥0
2、随机矩阵,每一行的值之和等于 1。
P
π
1
=
1
,
1
=
[
1
,
⋯
,
1
]
T
P_\pi \bm 1=\bm 1, ~~\bm 1=[1, \cdots,1]^T
Pπ1=1, 1=[1,⋯,1]T
状态转移矩阵:
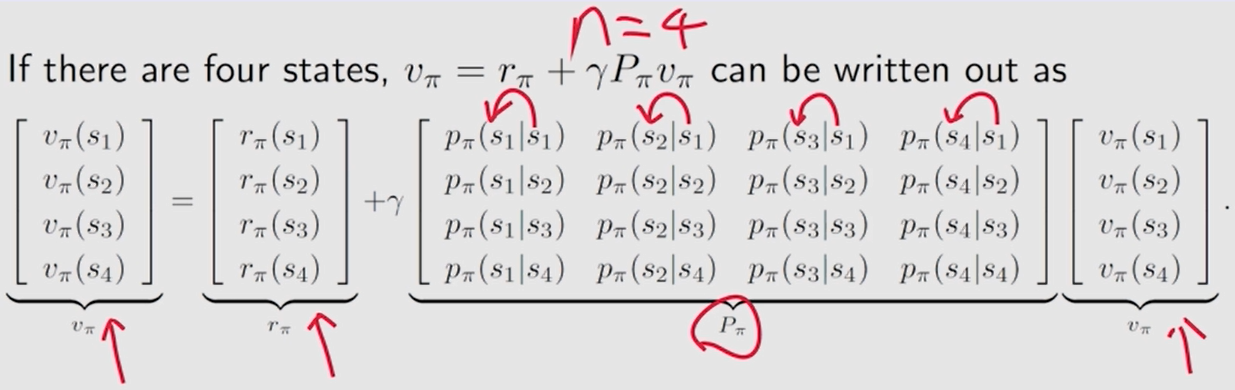
计算示例 1:
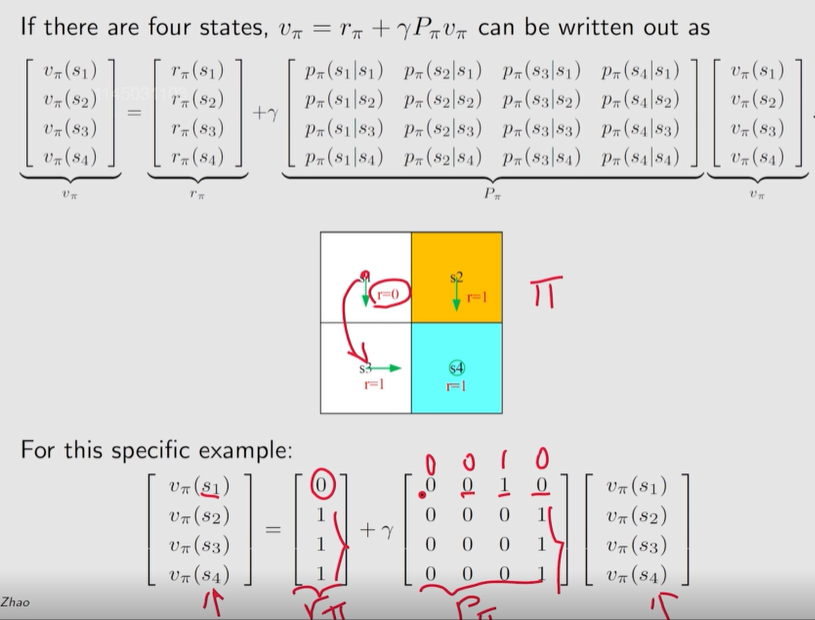
计算示例 2:
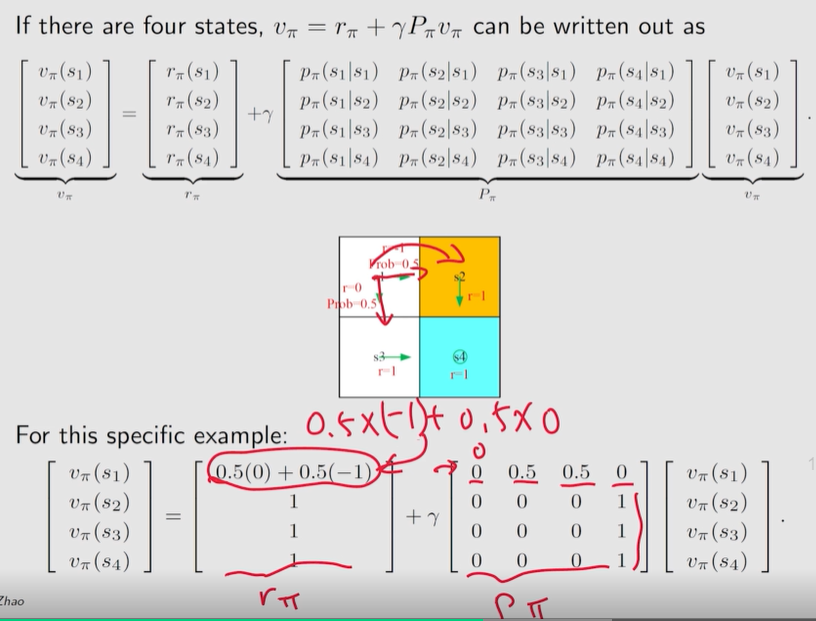
观察发现, P π P_\pi Pπ 每一行的值之和等于 1。 P π 1 = 1 , 1 = [ 1 , ⋯ , 1 ] T P_\pi \bm 1=\bm 1, ~~\bm 1=[1, \cdots,1]^T Pπ1=1, 1=[1,⋯,1]T
2.7 求解 贝尔曼公式 —> 求得 状态值
为什么要 求状态值?
给定一个策略,找出相应的状态值称为策略评估!这是找到更好策略的基础。
求解 贝尔曼方程 是进行策略评估的 重要步骤。


- P38

——————————————————————

证明: v k v_k vk 最终 收敛到 v π v_\pi vπ
归纳法
定义 误差 Δ k = v k − v π \Delta_k = v_k-v_\pi Δk=vk−vπ, 只需证明 Δ k → 0 \Delta_k\to0 Δk→0
将用到的等式
① 贝尔曼公式 v π = r π + γ P π v π v_\pi = r_\pi + \gamma P_\pi v_\pi vπ=rπ+γPπvπ
② v k + 1 = Δ k + 1 + v π v_{k + 1} =\Delta_{k +1}+v_\pi~~~~~ vk+1=Δk+1+vπ 误差定义
③ v k = Δ k + v π v_k=\Delta_k+v_\pi~~~~~ vk=Δk+vπ 误差定义
————————
v k + 1 = r π + γ P π v k v_{k + 1} = r_\pi + \gamma P_\pi v_k~~~~~ vk+1=rπ+γPπvk 迭代式
——> Δ k + 1 + v π = r π + γ P π ( Δ k + v π ) \Delta_{k +1}+v_\pi=r_\pi+\gamma P_\pi(\Delta_k+v_\pi) ~~~~~ Δk+1+vπ=rπ+γPπ(Δk+vπ) ②③
——> Δ k + 1 = − v π + r π + γ P π Δ k + γ P π v π = γ P π Δ k \Delta_{k +1}= -v_\pi+r_\pi+\gamma P_\pi\Delta_k+\gamma P_\pi v_\pi =\gamma P_\pi\Delta_k~~~~~ Δk+1=−vπ+rπ+γPπΔk+γPπvπ=γPπΔk ①
迭代递推
Δ k + 1 = γ P π Δ k = γ 2 P π 2 Δ k − 1 = γ 3 P π 3 Δ k − 2 = . . . = γ k + 1 P π k + 1 Δ 0 \Delta_{k +1}=\gamma P_\pi\Delta_k=\gamma^2 P_\pi^2\Delta_{k-1}=\gamma^3 P_\pi^3\Delta_{k-2}=...=\gamma ^{k+1}P_\pi^{k+1}\Delta_0 Δk+1=γPπΔk=γ2Pπ2Δk−1=γ3Pπ3Δk−2=...=γk+1Pπk+1Δ0
~
例子:
比较好的策略:
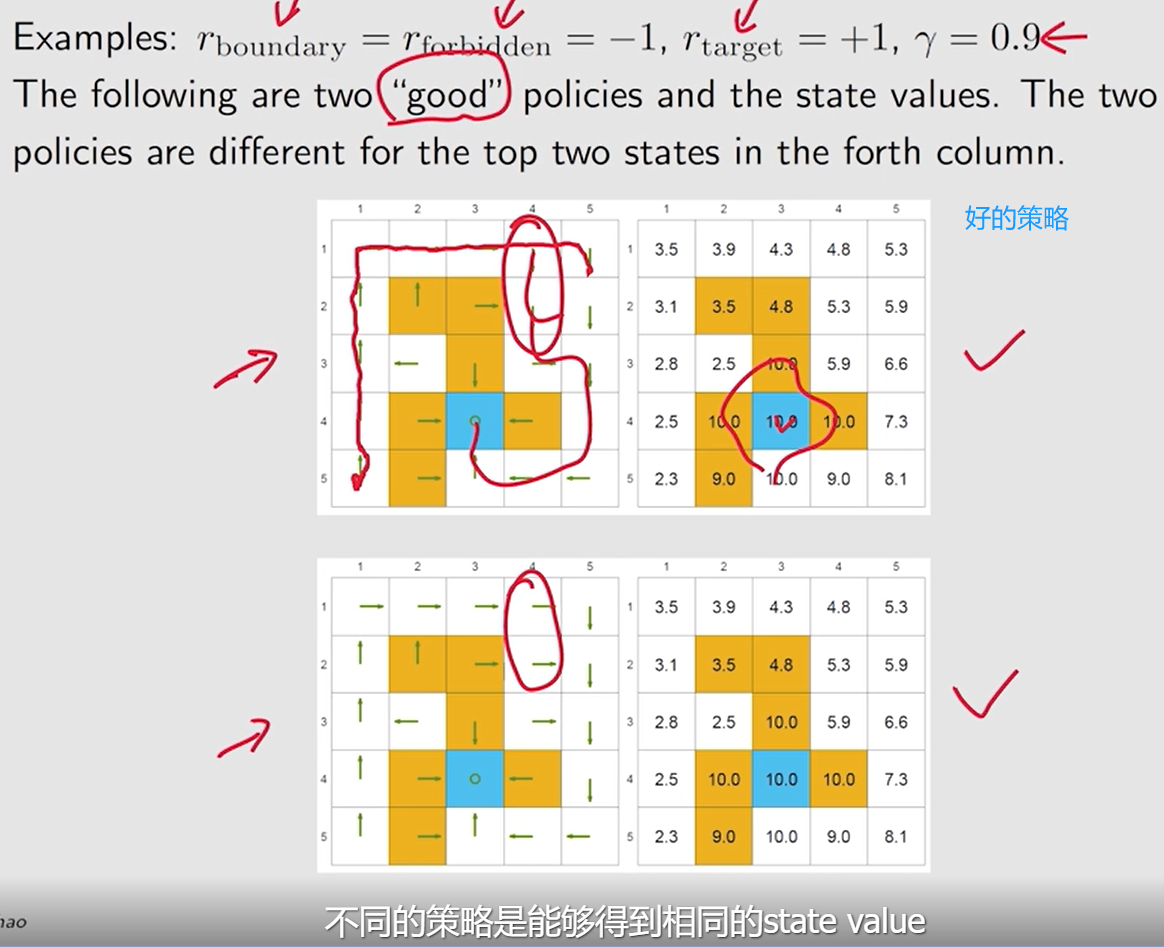
不同的策略可能具有相同的状态值。
离 目标区域 越近, 状态的状态值越大。
不太好的策略:
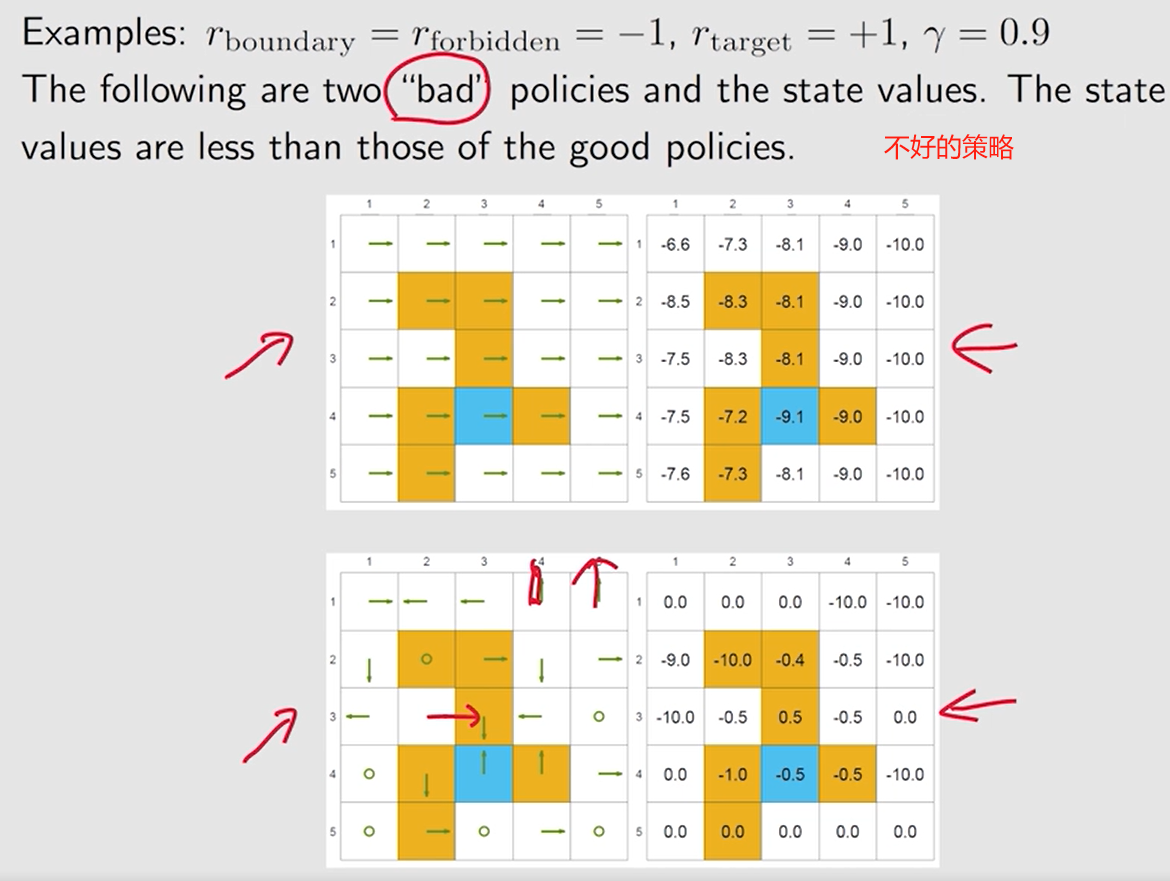
状态值 大多为 负数
——> 可以 计算 状态值 来评价一个策略的好坏。
2.8 Action value 动作值 q π ( s , a ) q_\pi(s, a) qπ(s,a)
状态值: 在某个状态 执行某个动作的价值 【回报期望值】
P5 Action value: 选哪个 action
State value VS Action value
State value:从 某个状态 出发 获得 的平均回报。 v π ( s ) v_\pi(s) vπ(s)
Action value: 从 某个状态 出发,执行 某个动作 后的平均回报。 q π ( s , a ) q_\pi(s, a) qπ(s,a)
在 一个状态中, 根据 action value 选择哪个 action。
action value 大 意味着 执行相应的 action 能获得更大回报。

v π ( s ) = ∑ a π ( a ∣ s ) q π ( s , a ) v_\pi(s)=\sum\limits_a\pi(a|s)q_\pi(s, a) vπ(s)=a∑π(a∣s)qπ(s,a)
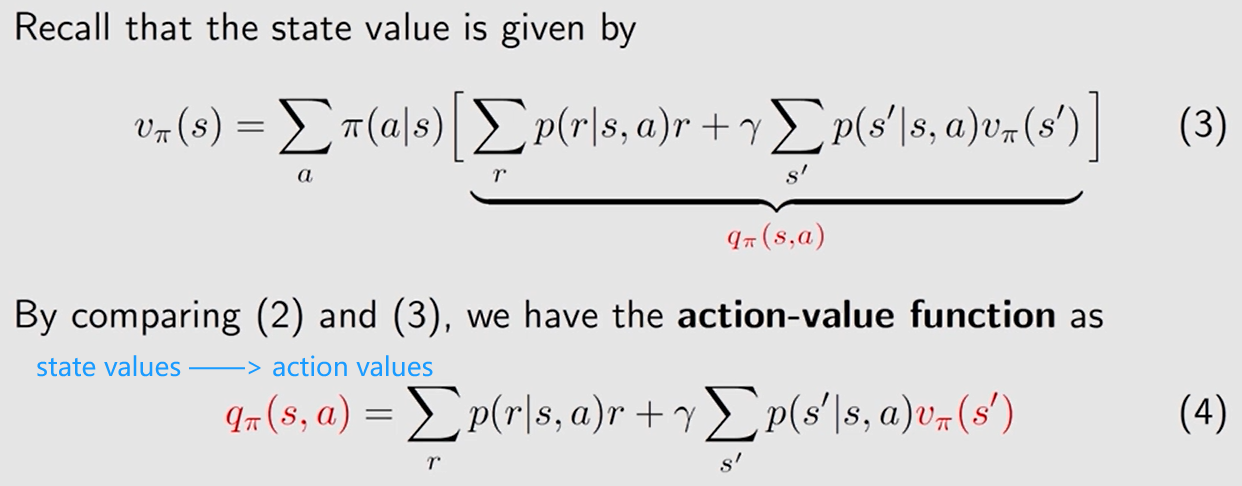
动作值 = 即时奖励的均值 + 未来奖励的均值。
例子:
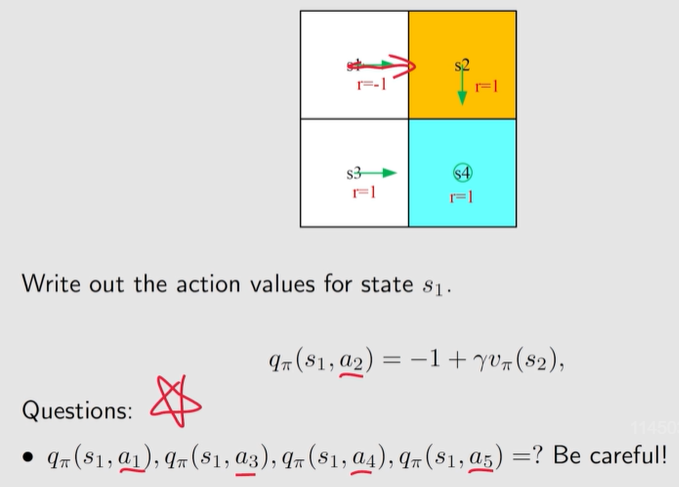
当前的策略规定 s1 要执行 向右 的动作, 但这个策略有可能不是最佳策略,仍需要计算 执行其它动作相应的 动作值, 为策略改进做准备。
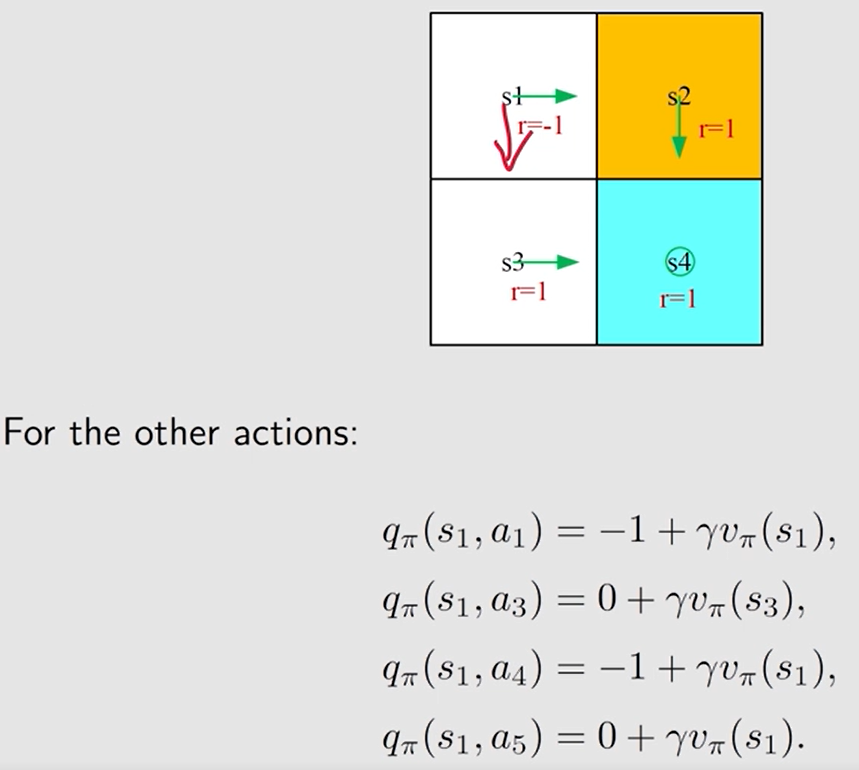
先计算 state values, 再计算 action values 。
在没有模型的情况下,通过数据直接计算 action values。
小结:
————————
PDF 补充:
基于 状态值 的 贝尔曼公式:
v π ( s ) = ∑ a π ( a ∣ s ) [ ∑ r p ( r ∣ s , a ) r + γ ∑ s ′ p ( s ′ ∣ s , a ) v π ( s ′ ) ] v_\pi(s)=\sum\limits_{a}\pi(a|s)\Big[\sum\limits_{r}p(r|s,a)r + \gamma \sum\limits_{s^\prime}p(s^\prime|s,a)v_\pi(s^\prime)\Big] vπ(s)=a∑π(a∣s)[r∑p(r∣s,a)r+γs′∑p(s′∣s,a)vπ(s′)]
2.8.2 动作值 的贝尔曼方程
q π ( s , a ) = ∑ r p ( r ∣ s , a ) r + γ ∑ s ′ p ( s ′ ∣ s , a ) ∑ a ′ ∈ A ( s ′ ) π ( a ′ ∣ s ′ ) q π ( s ′ , a ′ ) q_\pi(s, a)=\sum\limits_rp(r|s, a)r+\gamma\sum\limits_{s^\prime}p(s^{\prime}|s,a)\sum\limits_{a^\prime \in\cal A(s^\prime)}\pi(a^\prime|s^\prime)q_\pi(s^\prime,a^\prime) qπ(s,a)=r∑p(r∣s,a)r+γs′∑p(s′∣s,a)a′∈A(s′)∑π(a′∣s′)qπ(s′,a′)
矩阵-向量形式:
q π = r ~ + γ P Π q π q_\pi=\widetilde r+\gamma P \Pi_{q_\pi} qπ=r +γPΠqπ
- [ P ] ( s , a ) , s ′ = p ( s ′ ∣ s , a ) [P]_{(s, a),s^\prime}=p(s^\prime|s,a) [P](s,a),s′=p(s′∣s,a)
- Π s ′ , ( s ′ , a ′ ) = π ( a ′ ∣ s ′ ) \Pi_{s^\prime,(s^\prime,a^\prime)}=\pi(a^\prime|s^\prime) Πs′,(s′,a′)=π(a′∣s′)
————————————
2.10
state value状态值 和 return回报 的关系: 状态值是 agent 从该状态出发所能获得的 回报的均值。
状态值 和 动作值的关系: 一方面,状态值是 该状态的 动作值的均值。另一方面,动作值 依赖于 agent 在采取动作后可能过渡到的下一个状态的状态值。
v
π
(
s
)
=
∑
a
π
(
a
∣
s
)
q
π
(
s
,
a
)
v_\pi(s)=\sum\limits_a\pi(a|s)\textcolor{blue}{q_\pi(s, a)}
vπ(s)=a∑π(a∣s)qπ(s,a)
q
π
(
s
,
a
)
=
∑
r
p
(
r
∣
s
,
a
)
r
+
γ
∑
s
′
p
(
s
′
∣
s
,
a
)
v
π
(
s
′
)
q_\pi(s, a)=\sum\limits_rp(r|s, a)r+\gamma\sum\limits_{s^\prime}p(s^\prime|s, a)\textcolor{blue}{v_\pi(s^\prime)}
qπ(s,a)=r∑p(r∣s,a)r+γs′∑p(s′∣s,a)vπ(s′)
—————————————————————————————————
习题笔记:
- State value:折扣回报的期望值。
- 状态值
v
π
(
s
)
v_\pi(s)
vπ(s) 和
策略、状态有关。不是 动作。 - 贝尔曼方程 描述了所有状态值之间的关系。
- 每一个状态都对应一个贝尔曼方程。
- 动作值(action value) q π ( s , a ) q_\pi(s, a) qπ(s,a) 和动作、状态和策略有关。



![[leetcode]add-strings 字符串相加](https://img-blog.csdnimg.cn/direct/e377a66a3ada4e9c922bdefa558f40b2.png)