0.快速排序

1.时间复杂度：O（N*logN）
稳定性：不稳定
整体综合性能和使用场景都比较好
空间复杂度：O（logN）

1.Hoare版本

1.1基本思想

通过一趟排序将待排记录分隔成独立的两部分，其中一部分记录的关键字均比另一部分的关键字小，则可分别对这两部分记录继续进行排序，以达到整个序列有序。

1.2算法描述

• 从数列中选出一个元素作为基准（一般都是第一个元素）
• 定义两个指针left，right。
• right先走，找小，找到小就停下来；left后走，找大，找到大就停下来。然后交换left和right对应的值。
• 重复上述操作，直到left和right相遇，停下来并交换相遇点的值和基准值。
• 以基准值分成了两个区间，递归地重复上述操作。

1.3画图解释

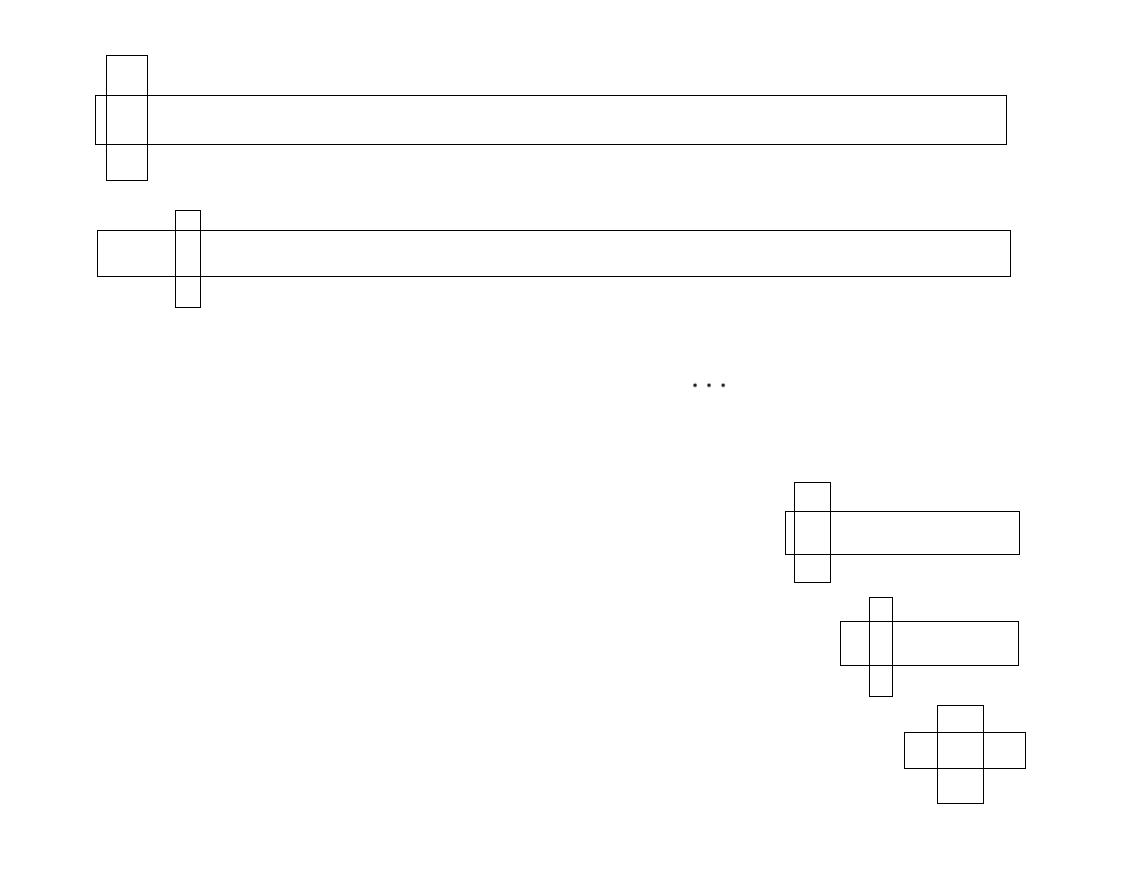
第一遍：
right先走，找小；left后走，找大
left和right相遇时，交换相遇点和基准对应的值
达到了分区间作用；左区间 < 基准 ，右区间 > 基准

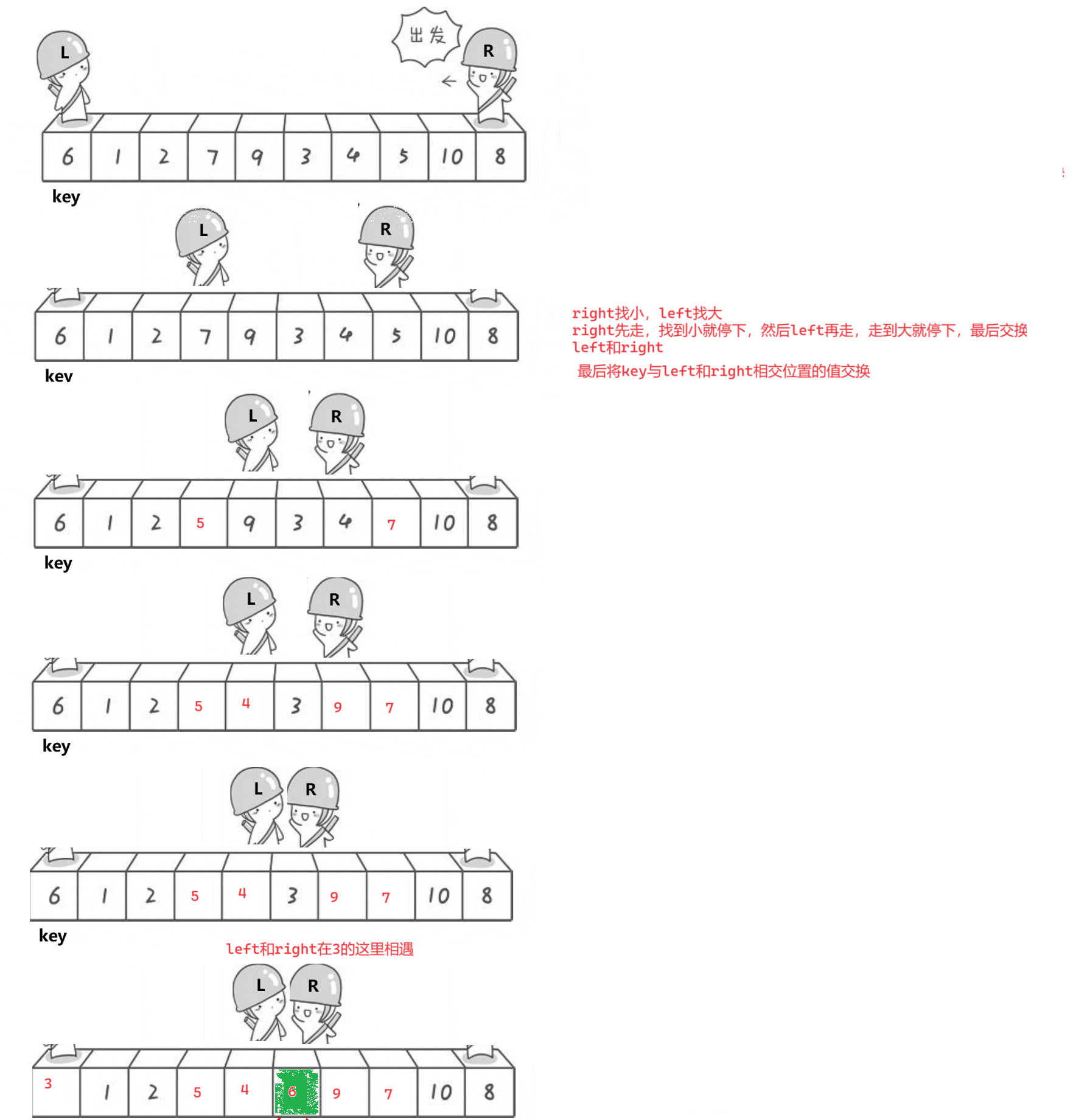
开始递归上述操作

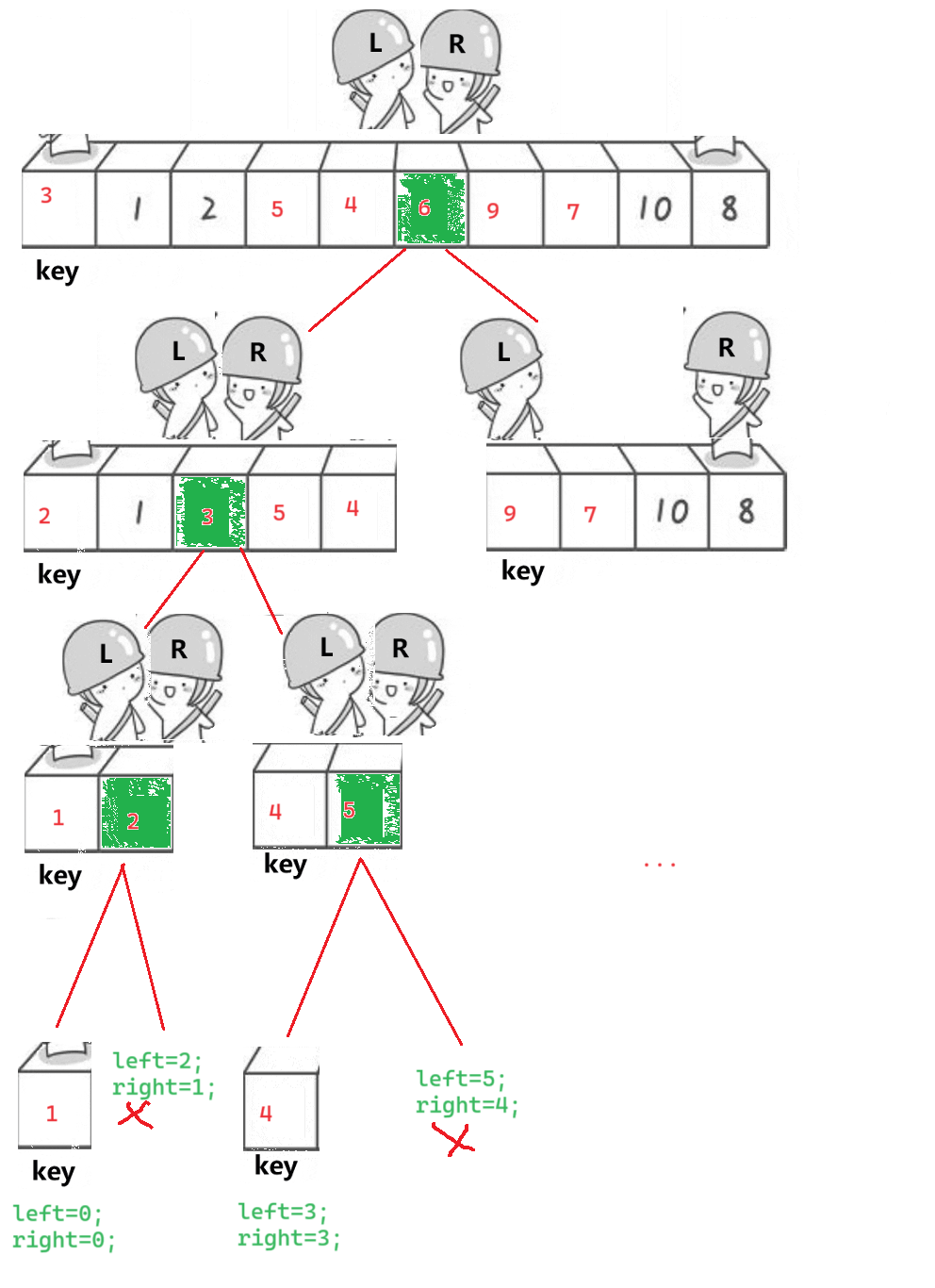
1.4问题？

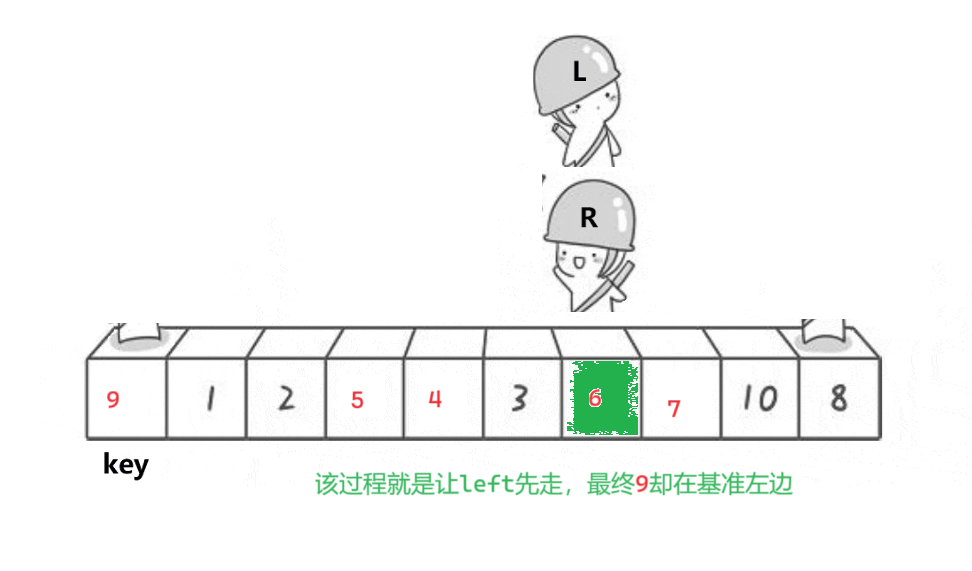
1.为什么要让right先走？如果left先走行不行？

让right先走最后可以满足比基准小的都在基准的左边，比基准大的都在基准的右边。
不行，如果left先走就不能满足上述条件

2.为什么left和right的相遇点对应的值一定小于等于基准？

left去遇见right：
right先走，找小，找到小就停下来；left后走，找大，找到大就停下来，两者对应的值发生交换；如果left没有找到与right发生相遇，所相遇点一定是小于基准的
right去遇见left：
right先走，找小，如果没有找到就一直走，直到和left相遇，此时相遇点所对应的值是小于基准的

1.5代码实现

// 快速排序hoare版本
void PartSort(int* a, int left, int right)
{
	if (left >= right)//表示该区间只有一个元素或者该区间不存在
		return;

	int begin = left;
	int end = right;
	int key = a[left];
	while (begin < end)
	{
		//先找小
		while (begin < end && a[end] > key)
			--end;
		//找大
		while (begin < end && a[begin] <= key)
			++begin;
		//交换begin和end位置的值
		swap(&a[begin], &a[end]);
	}
	//begin和end相遇
	swap(&a[begin], &a[left]);//swap(&a[begin,&key);两值会交换，但是系统并不知道key对应数组中第几个数据
	//[left,begin-1]  begin  [begin+1,right]
	PartSort12(a, left, begin - 1);
	PartSort12(a, begin + 1, right);
	
}

2.挖坑法

2.1算法描述

• 把第一个数据存放在一个临时变量key中，形成坑位
• right先走，找小，找到小就停下来
• 将right所对应的值，放在坑位中，right形成新的坑位
• left后走，找大，找到大就停下来
• 将left所对应的值放在坑位中，left形成新的坑位
• 当left和rihgt相遇时，两者都处在坑位位置，把临时变量key放到坑位中
• 分区间递归

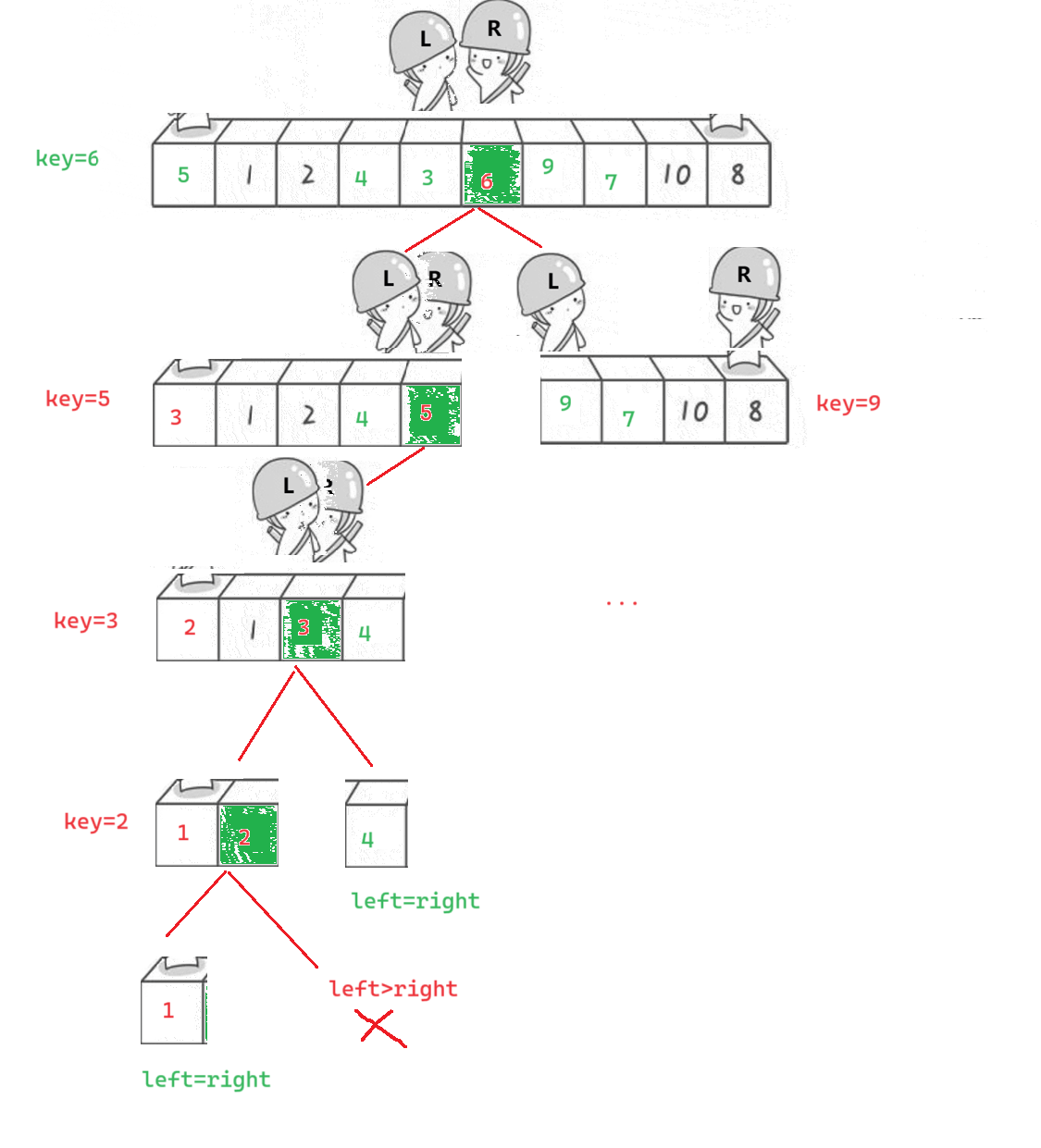
2.2画图解释

第一遍：
先将第一个数据放在一个临时变量（key）中形成坑位
right先走，找到小就放到坑位中去，right处形成新的坑位
left后走，找到大就放在坑位中去，left处形成新的坑位
分区间：左区间 < key ；右区间 > key

第二遍：递归重复上述操作

2.3代码实现

// 快速排序挖坑法
void PartSort2(int* a, int left, int right)
{
	//表示该区间只有一个元素或者该区间不存在
	if (left >= right)
		return;

	//创建一个临时变量存放第一个数据的值，形成坑位
	int key = a[left];
	int begin = left;
	int end = right;
	while (begin < end)
	{
		while (begin<end && a[end]>key)
			--end;
		a[begin] = a[end];
		while (begin < end && a[begin] <= key)
			++begin;
		a[end] = a[begin];
	}
	//begin和end相遇
	a[begin] = key;
	//[left,begin-1] begin [begin+1,right]
	PartSort2(a, left, begin - 1);
	PartSort2(a, begin+1, right);
}

3.先后指针法

3.1算法描述

• 初始时，prev指到序列的开头，cur指到序列的下一个位置
• 先判断cur位置对应的值和key（序列开头位置）的大小
• 比key小 ++prev 将prev和cur所对应的值进行交换，然后++cur
• 如果比key大，直接++cur
• 当cur越界时，将key的值和prev的值进行交换

3.2画图解释

第一遍：prev指到序列的开头，cur指到序列的下一个位置
判断cur所对应的值与key的大小

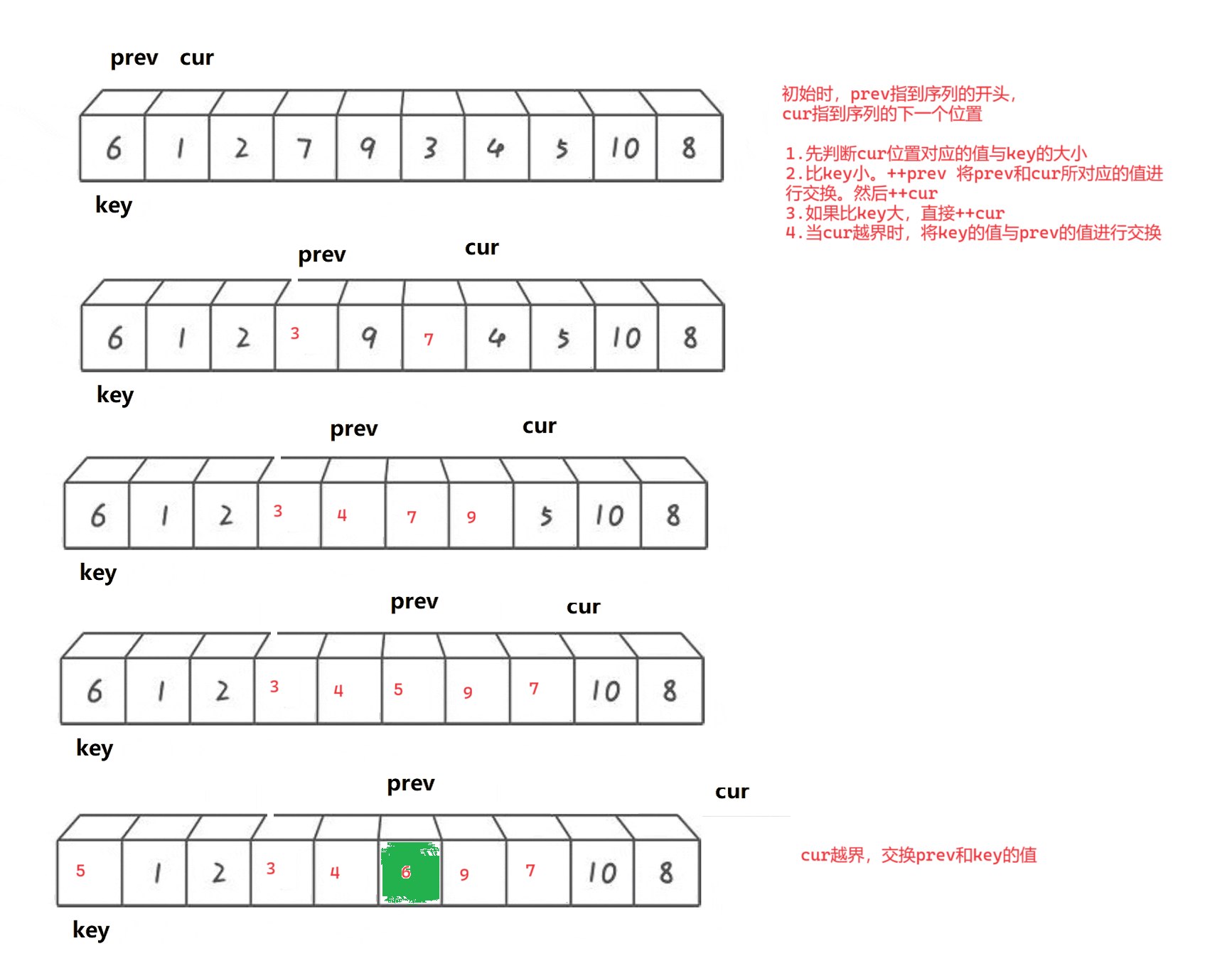
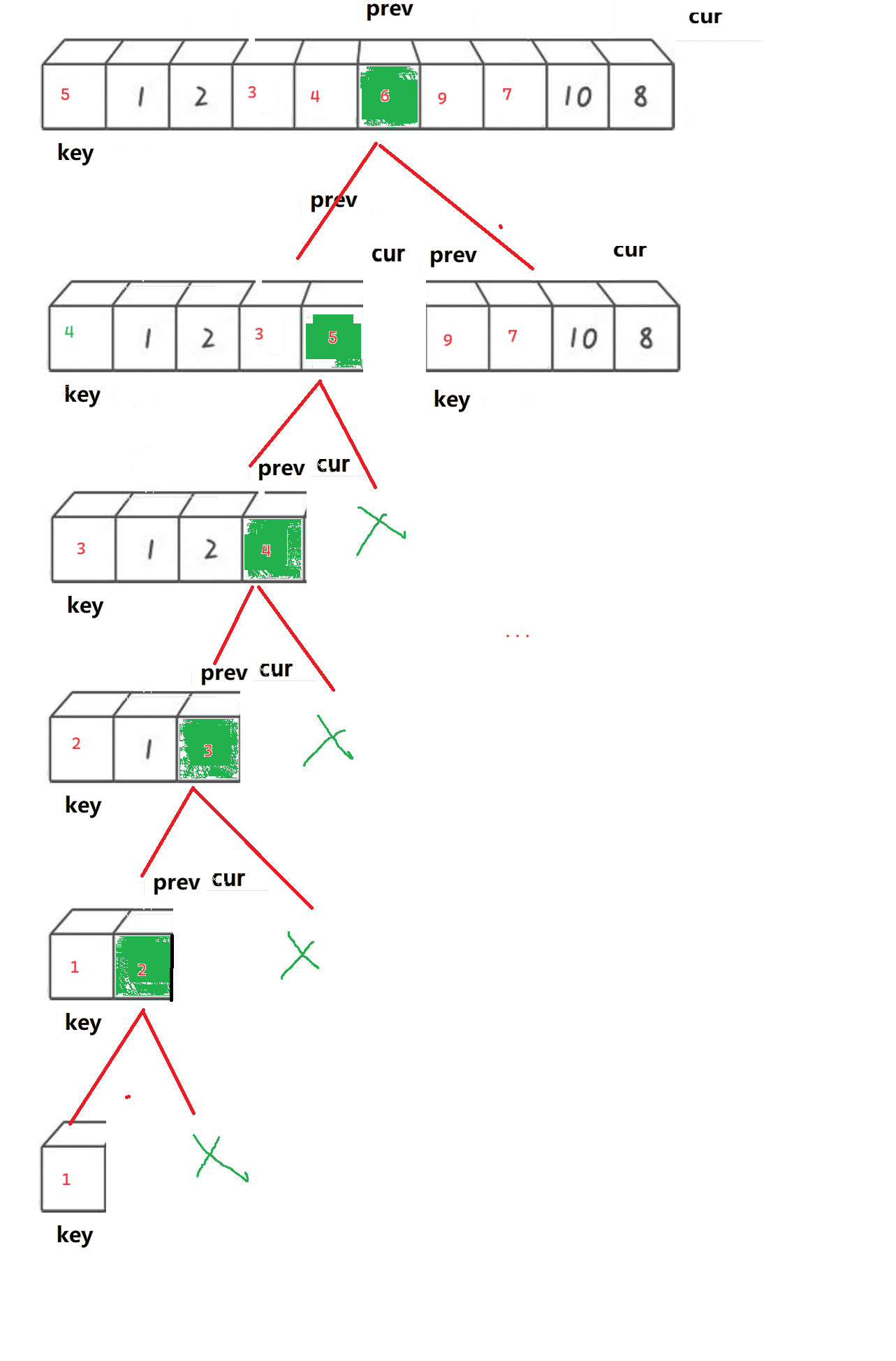
递归重复上述操作

3.3代码实现

// 快速排序前后指针法
void PartSort3(int* a, int left, int right)
{
	//表示该区间只有一个数据或者该区间不存在
	if (left >= right)
		return;

	int begin = left;
	int end = right;
	int prev = begin;
	int cur = begin+1;
	int key = a[begin];
	while (cur <= end)
	{
		if (a[cur] < key)
		{
			++prev;
			swap(&a[cur], &a[prev]);
		}
		++cur;
	}
	//交换prev和key位置的值
	swap(&a[prev], &a[begin]);
	//[begin,prev-1] prev [prev+1,end]
	PartSort3(a, begin, prev - 1);
	PartSort3(a, prev+1,end);

}

4.优化

4.1优化方法

1.三数取中
2.小区间优化

1.为什么要进行三数取中？

当序列有序时，会加大快速排序所用的时间。分区间的时候，可能出现下面这种情况

int Mid(int* a, int left, int right)
{
	int mid = left + ((right - left) >> 1);
	if (a[left] > a[mid])
	{
		if (a[mid] > a[right])
			return mid;
		else if (a[left] > a[right])
			return right;
		else
			return left;
	}
	else//a[left]<a[mid]
	{
		if (a[right] > a[mid])
			return mid;
		else if (a[left] > a[right])
			return left;
		else
			return right;
	}
}

2.小区间优化

防止递归深度太深，栈溢出。同时可以减少所用时间。

4.2优化代码

void QuickSort(int* a, int left, int right)
{
	if (left >= right)
		return;

	
	//小区间优化
	//如果一个区间内的数据小于10个就进行小区间优化
	if ((right - left + 1) < 10)
	{
		InsertSort(a+left, right - left + 1);
	}
	else
	{
		//三数取中
		int mid = Mid(a, left, right);
		swap(&a[mid], &a[left]);

		int t = PartSort1(a, left, right);
		//[left,t-1] t [t+1,right]
		QuickSort(a, left, t - 1);
		QuickSort(a, t + 1, right);
	}
}

5.非递归实现快排

5.1算法描述

• 建栈
• 先将序列的left和right压入栈中
• 再取出栈顶的left和right进行（挖坑法或前后指针法）
• 再分区间把left和right压入栈中
• 直到栈为空为止
  

下面代码只有具体过程，没有与栈相关的代码

#include "Stack.h"
// 快速排序 非递归实现
void QuickSortNonR(int* a, int left, int right)
{
	ST st;
	StackInit(&st);
	//先压入right，再压入left
	StackPush(&st, right);
	StackPush(&st, left);

	while (!StackEmpty(&st))
	{
		int begin = StackGet(&st);
		StackPop(&st);
		int end = StackGet(&st);
		StackPop(&st);

		int keyi = PartSort1(a, begin, end);//分区间的点
			
		//[begin,keyi-1] keyi [keyi+1,end]
		//该区间不存在或者只有一个数据就不用压入栈中了
		if (begin < keyi - 1)
		{
			StackPush(&st,keyi - 1);
			StackPush(&st, begin);
		}
		if (keyi + 1 < end)
		{
			StackPush(&st,end);
			StackPush(&st, keyi + 1);
		}
	}
	StackDestory(&st);
}