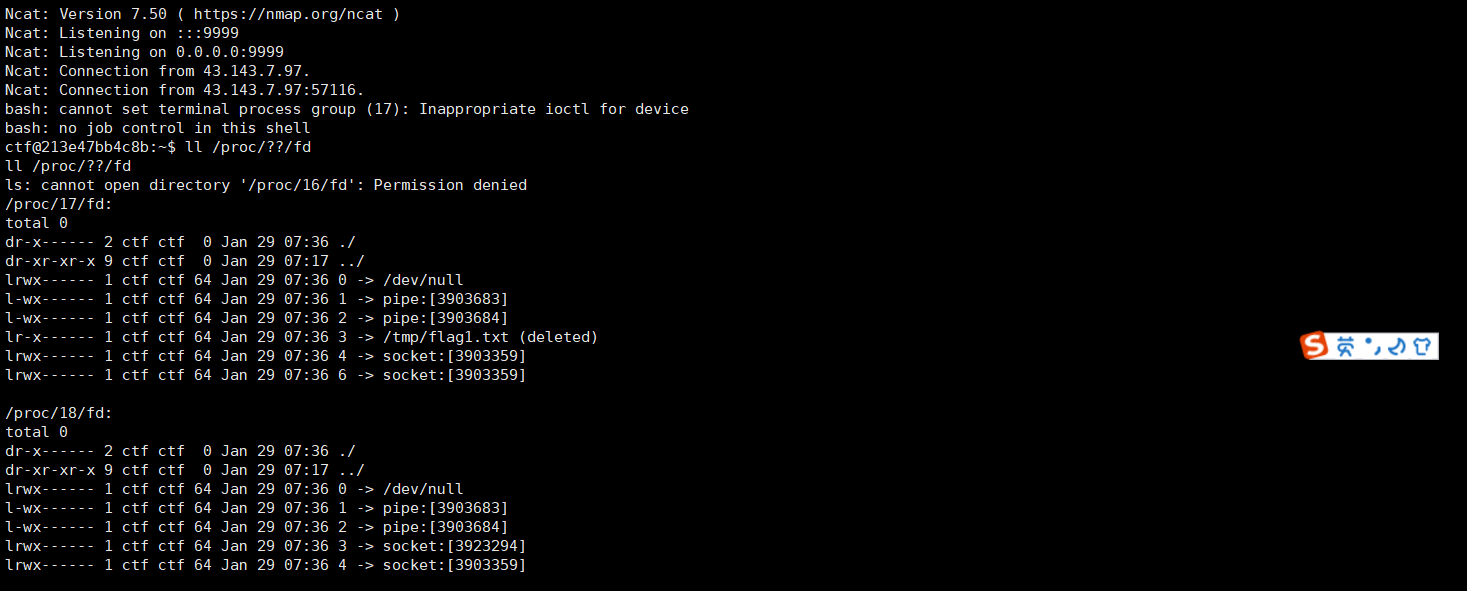
​结合亲和力具有自由能的分子基础理论：在本章中，我们使用K来衡量结合亲和力。我们可以通过结合曲线(binding curves,)来像这样定义一个结合作用力。这样的曲线能给出配体结合的数量与溶液中配体数量的关系。而结合亲和力K也存在关于分子结构以及能量基础。K来自于蛋白质结合位点的溶剂被取代以及配体和蛋白质结合位点所产生的的稳定的原子间结合力。为了将结合亲核力与分子结构和能量这两个方便结合，我们可以使用自由能ΔG来展示其对应的结合过程：

通过用自由能来表达结合，我们现在有了一种语言来理解结合过程如何与其他类型的蛋白质过程相关的现象如：机械力和功，电势，光和辐射等。这是因为自由能是能量因子和熵因子的总和，而蛋白质对它们很敏感。图4.12是机械力如何导致力×位移、压力×面积和电荷×静电势f的乘积变化的卡通图。这些过程的能量和熵，以及从第一性原理物理模型计算它们的方法，将在别处描述（见[1]的第9章和第10章）。

图4.12 结合过程可以与其他类型的力相耦合。不同类型的自由能可以相互耦合，导致另一个作用的转导。(A)结合过程。机械力导致(B)力×位移、(C)压力×面积和(D)电荷×静电势乘积的变化。

-抑制剂和激活剂可以调节其他的结合活动

目前为止，我们只对含有一种特定的配体的结合过程进行阐述。在血红蛋白的结合过程中，我们也只是说到了这个蛋白质与氧的结合过程。而现在，我们开始要考虑不同化学类型配体的结合过程。比如，血红蛋白既可以结合氧气也可以结合二氧化碳。但是结合了二氧化碳会阻止血红蛋白结合氧气。从而导致中毒或者窒息。接下来，让我们一起了解涉及到不同类型配体的蛋白结合过程(图4.13)。

图4.13 抑制作用的类型。(A)竞争性抑制剂Y竞争X结合的P位点.(B)结合的位点，非竞争性抑制剂Y不会结合，除非配体X也结合。例如，(C)非竞争性抑制剂Y对X与P的结合没有影响，因为它在一个独立的位点结合。

有些分子式具有竞争性的。假设一个分子P的结合位点可以与某一类型的配体X以K的结合力进行结合。此时，另一类型的配体Y以结合力R也可以在这个分子的同一位点结合：

假设两种配体的溶液浓度分别为x = [X]和y = [Y],那么其结合多项式为：

在这个溶液中，P的结合位点要么是自由的，要么就和X结合，要么和Y结合。那么P位点上的x平均占比为(νX = (∂ ln Q/∂ ln x))：

同理，我们也可以获得Y的平均占比。而这个时候，Y就就是X的竞争性抑制剂：因为它会和X竞争分子P上的结合位点。图4.14显示了这种抑制作用：随着Y的浓度或亲和力的增加，X结合的数量减少。此外，公式4.33也适用于那些可以通过取代其配体来破坏一个表面或催化剂的杂质。

图4.14 在竞争抑制剂Y存在的情况下，配体X的结合等温线，其中的曲线为三个水平的Y：（棕色）最高的Y，（红色）最低的Y，和（蓝色）中间的Y。

结合多项式可以告诉我们所有可能存在的状态的总体，以及结合的有无。但它们不会告诉我们哪些结合状态会产生活性效果的。考虑两种不同的场景。首先，在之前的模型中，假设P的生物学作用只发生在P与X结合时而非与Y结合时。然后，生物作用将与νX相关，而Y则会抑制这种作用。但另一种可能性是，当P与配体X或y结合时，它的活性都会产生，就像：

那么，在第二种场景中，Y是一种激活剂而非一种抑制剂。激活剂是一种促进另一种分子结合的分子；参见box4.5中的例子。为了计算分子的作用性质，我们需要知道结合多项式中的哪些项负责活性的作用。结合多项式本身并不能告诉我们这一点；我们需要关于作用机制的知识。

这里还有其他的结合机制：只有当X已经与P结合了，Y才会和P结合。

那么，我们的结合多项式就会变成：

那么p的状态就会有要么结合位点是空的，要么结合位点与X结合，要么结合位点同时与P和X结合。配体Y不能单独存在，而每个分子P上的X平均占比：

但是呢，有时候X和Y并不存在竞争性，他们分别在不同的位点结合：

那么，结合多项式为：

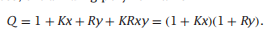
在非竞争性抑制剂模型中，X与P的结合独立于Y与P的结合，有时是因为这两个配体与独立的位点结合。例如，硝苯地平是一种治疗高血压的钙通道阻滞剂药物；它是cyp2c9的非竞争性抑制剂，cyp2c9是细胞色素P450蛋白家族的一个成员，负责几种临床重要药物的代谢。

-------------------------------------------

欢迎点赞收藏转发！

下次见！