小欧的平均数

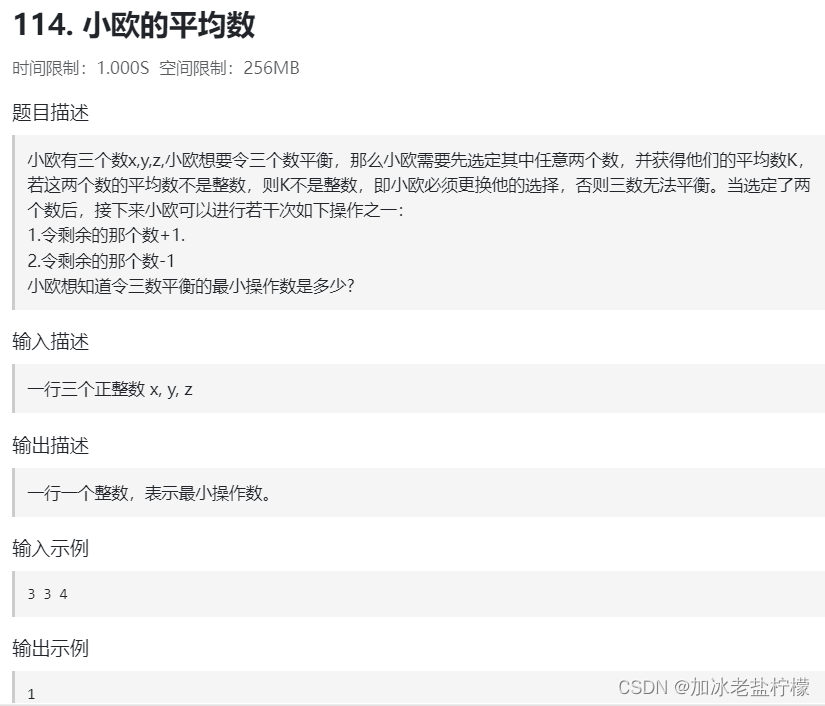
这道题不看解析的话完全没有思路，连题目都没读明白，甚至看了评论答出来了还是不知道为什么，有知道的朋友可以教教我

#include<iostream>
using namespace std;

int main()
{
    int x,y,z;
    cin>>x>>y>>z;
    
    //求全部变为奇数或者全部变为偶数的最小操作次数
    int result=(x%2==0)+(y%2==0)+(z%2==0);
    if(result>3-result)
    {
        result=3-result;
    }
    cout<<result<<endl;
}