论文地址: EfficientNet: Rethinking Model Scaling for Convolutional Neural Networks

1、abstract

提出了一种新的尺度方法，使用简单而有效的复合系数均匀地调整深度/宽度/分辨率的所有维度（Compound Model Scaling复合模型缩放）。并在MobileNets和ResNet上验证了有效性。

采用一组固定的比例系数均匀缩放网络的width、depth和resolution。

使用神经架构搜索来设计一个新的baseline，并扩展了一系列模型，称为EfficientNets。

优势：

（1）在ImageNet上实现了最先进的84.3%的top-1精度。

（2）比现有最好的ConvNet小8.4倍，推理速度快6.1倍。

（3）在CIFAR-100（91.7%）、Flowers（98.8%）和其他3个迁移学习数据集上精度最好，且参数量小。

2、Compound Model Scaling

​

深度：神经网络的层数
宽度：每层的通道数
分辨率：是指网络中特征图的分辨率
深度学习中模型计算量(FLOPs)和参数量(Params)的理解以及四种计算方法总结

​一个卷积网络层（ConvNet）通过一系列的操作来处理输入数据。可以用数学表达式表示为：$Y_i=F_i(X_i)$。这里，$F_i$ 是第i层的运算符，$Y_i$ 是输出张量（即该层处理后的输出数据），$X_i$ 是输入张量（即该层接收的输入数据）。

每个张量都有特定的形状，用尖括号标记为$<H_i,W_i,C_i>$。这里的$H_i$ 和 $W_i$ 分别表示空间维度的高度和宽度，而$C_i$ 是通道维度，可能代表颜色通道（如RGB）或其他特征通道。

整个卷积网络N可以通过一系列组合的层级来表示，用数学表达式表示为：$N=F_k\odot \dots \odot F_2\odot F_1(X_1)={\odot }_{j=1\dots k}{F}_j(X_1)$。这个表达式说明，网络N由k层组成，每一层都以前一层的输出作为输入，并将自己的输出传递给下一层。符号$\odot$ 表示函数的复合，即一个函数的输出成为下一个函数的输入。

在实际应用中，为了提高计算效率和模型性能，卷积网络的层级通常会被分成多个阶段，同一个阶段内的所有层级共享相同的架构。例如，ResNet（深度残差网络）有五个阶段，每个阶段内所有层级的卷积类型相同，但第一个层级会执行下采样以减少数据的空间维度。

因此，可以将一个卷积网络定义如下：

$$N=\underset{i=1\dots s}{⨀}{F}_i^{L_i}(X_i)$$

其中，$F_i^{L_i}$ 表示在第i阶段重复使用层级$F_i$共$L_i$次，$<H_i,W_i,C_i>$ 表示第i层的输入张量$X$的形状。

通常关注于寻找最佳层级架构$F_i$的ConvNet设计不同，模型扩展试图在不改变基线网络中预先定义的$F_i$的情况下，扩展网络的长度$(L_i)$、宽度$(C_i)$和/或分辨率$(H_i,W_i)$。通过固定$F_i$，模型扩展简化了新资源约束下的设计问题，但仍有很大的设计空间来探索每层的$L_i、C_i、H_i、W_i$。

为了进一步减少设计空间，本文将所有层按恒定比例统一缩放。目标是在给定的资源约束下最大化模型准确性，这可以表述为一个优化问题：
$$\underset{d,w,r}{\max }Accuracy(N(d,w,r))$$
受限于（公式（2））：
$$\begin{array}{rl}N(d,w,r)& ={\odot }_{i=\mathrm{1...}s}{\hat{F}}_i^{d\cdot {\hat{L}}_i}(X_{r\cdot {\hat{H}}_i,r\cdot {\hat{W}}_i,w\cdot {\hat{C}}_i})\\ Memory(N)& \le \text{target\_memory}\\ FLOPS(N)& \le \text{target\_flops}(2)\end{array}$$
其中，w、d、r是用于缩放网络宽度、深度和分辨率的系数；${\hat{F}}_i$、${\hat{L}}_i$、${\hat{H}}_i$、${\hat{W}}_i$、${\hat{C}}_i$是基线网络中预定义的参数（见表1为例）。

缩放网络的宽度、深度和像素是卷积神经网络中的关键概念，它们共同决定了网络的性能和效率。

1. 缩放网络的深度：这是网络中所有卷积层的数量总和。网络深度影响其学习能力，更深的网络能够学习更复杂的特征。随着层数的增加，网络可以逐层提取从简单到复杂的特征。例如，第一层可能学习边缘特征，而更深层可能学习特定形状或对象的高级特征。

2. 缩放网络的宽度：这指的是单个卷积层内部的卷积核数量或通道的数量。增加宽度可以使每一层学习到更加丰富的特征，如不同方向、频率和颜色的纹理特征。但是，宽度过大会导致计算量的显著增加，并可能带来过多的重复特征，从而影响网络效率。（能够捕获更细粒度的特征，并且更容易进行训练）然而，非常宽但较浅的网络往往难以捕获更高层次的特征。在图3（左）中的结果显示，当网络越大，w变得越宽时，精度迅速饱和.

3. 缩放网络的像素：这通常指输入图像的分辨率，即图像的宽度和高度的像素数量。在卷积神经网络中，分辨率会影响特征图的大小。高分辨率图像能提供更多的细节信息，但同时也会增加计算负担。通过卷积和池化操作，网络会逐步减小特征图的分辨率，同时增强特征的抽象级别。
   
   为了比较了不同网络深度和分辨率下的宽度缩放，如图4所示。如果只扩展网络宽度w(d=而不改变深度（1.0）和分辨率（r=1.0），精度就会迅速饱和。通过更深的（d=2.0）和更高的分辨率（r=2.0），宽度扩展在相同的FLOPS损失下获得了更好的精度。
   
   **公式（3）：**为了追求更好的精度和效率，在连续网络缩放过程中，平衡网络宽度、深度和分辨率的所有维度都是至关重要的。本文提出了一种新的复合缩放方法，该方法使用一个复合系数 $\varphi$ 来统一地调整网络的宽度、深度和分辨率：
   $$depth:d={\alpha }^{\varphi }$$
   $$width:w={\beta }^{\varphi }$$
   $$resolution:r={\gamma }^{\varphi }$$
   $$s.t.\alpha \cdot {\beta }^2\cdot {\gamma }^2\approx 2$$
   $$\alpha \ge 1,\beta \ge 1,\gamma \ge 1$$
   其中 $\alpha ,\beta ,\gamma$ 是可以通过小规模网格搜索确定的常数。直观上，$\varphi$ 是一个用户指定的系数，用于控制模型扩展时可用资源的增加量，而 $\alpha ,\beta ,\gamma$ 分别指定如何将这些额外资源分配给网络的宽度、深度和分辨率。值得注意的是，常规卷积操作的 FLOPS 与 $d,w^2,r^2$ 成正比，即网络深度翻倍将使 FLOPS 翻倍，但网络宽度或分辨率翻倍将使 FLOPS 增加四倍。由于卷积操作通常在 ConvNets 中占据计算成本的主导地位，因此 对 ConvNet 进行缩放将大致使总 FLOPS 增加 $(\alpha \cdot {\beta }^2\cdot {\gamma }^2{)}^{\varphi }$。在本文中，我们约束 $\alpha \cdot {\beta }^2\cdot {\gamma }^2\approx 2$，以便对于任何新的 $\varphi$，总 FLOPS 大约增加 $2^{\varphi }$。

3、EfficientNet Architecture

第一步：假设资源增加两倍，固定$\varphi =1$，并在等式2和3的基础上对$\alpha$、$\beta$、$\gamma$进行小范围网格搜索。找到EfficientNet-B0的最佳值分别为$\alpha =1.2$、$\beta =1.1$、$\gamma =1.15$，约束条件为$\alpha \cdot {\beta }^2\cdot {\gamma }^2\approx 2$。
第二步：将$\alpha$、$\beta$、$\gamma$作为常数，使用等式3通过不同的$\varphi$放大基线网络，得到EfficientNet-B1至B7（详情见表2）。
此外，在较大模型周围直接搜索$\alpha$、$\beta$、$\gamma$可能会获得更好的性能，但大模型上的搜索成本过于昂贵。于是通过只在小型基线网络上进行一次搜索（第一步），然后对所有其他模型使用相同的缩放系数（第二步）来解决这个问题。
下面为EfficicentNet-B0基线网络结构：

4、results

将缩放方法应用于MobileNets和ResNet。表3显示了以不同方式缩放的ImageNet上结果。与其他单点缩放方法相比，复合缩放方法提高了所有模型的精度。

图5展示了EfficientNet比ConvNets拥有更高的精度和更少的参数量、并且计算成本更低。

表4展示了模型的推理速度比较

表5展示了模型迁移学习的效果：
(1) 与NASNet-A和Inception-v4等公开模型相比，EfficientNet模型在平均减少4.7倍（最多21倍）参数的情况下，实现了更高的准确率；
(2) 与包括DAT 和GPipe在内的最先进模型相比，EfficientNet在8个数据集中的5个上准确率更高，但使用的参数减少了9.6倍。

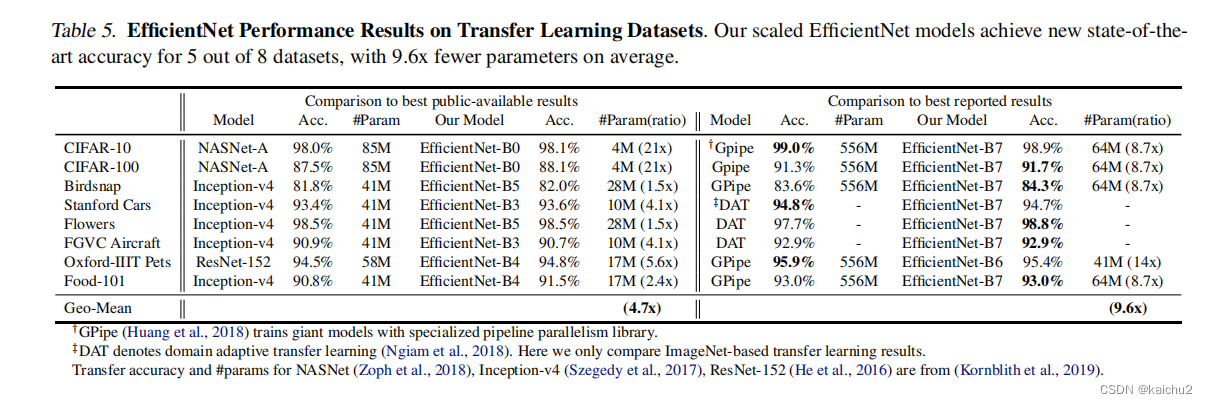
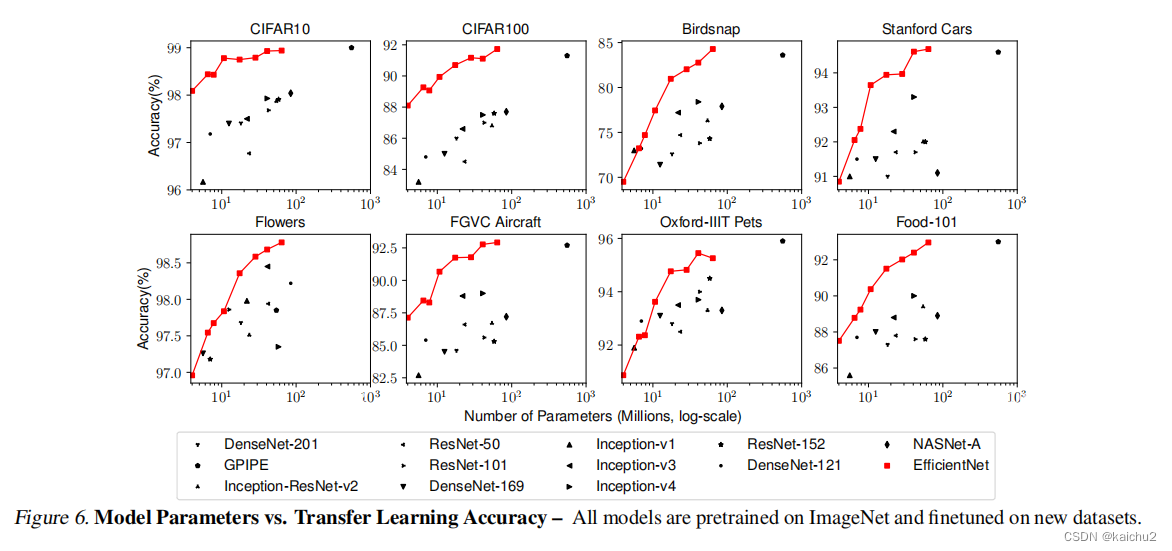
图6展示了EfficientNet与各个模型的精度和参数的对比曲线，全面领先。

5、conclusion

本文系统地研究了卷积网络的缩放，并确定平衡网络的宽度、深度和分辨率是重中之重，并且限制了准确性和效率。为了解决这个问题，提出了一种简单而高效的复合缩放方法，它能够轻松地将基线卷积网络扩展到任何目标资源约束下，同时保持模型效率。在这种复合缩放方法的支持下，证明了EfficientNet模型可以非常有效地放大，以小参数量和FLOPS上实现精度的遥遥领先。