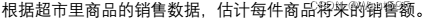吴恩达机器学习第三课 week1 无监督学习算法（下）

01 学习目标

02 异常检测算法

2.1 异常检测算法的概念

2.2 基于高斯模型的异常检测

03 利用异常检测算法检测网络服务器的故障

3.1 问题描述

3.2 算法实现

3.3 问题升级

04 总结

01 学习目标

（1）理解异常检测算法（Anomaly Detection Algorithm）的原理

（2）利用异常检测算法检测网络服务器的故障。

02 异常检测算法

2.1 异常检测算法的概念

异常检测算法不是指某一特定算法，而是实现异常检测功能的算法统称，旨在识别数据集中不符合常规模式的数据点，如欺诈检测、网络安全、故障预测、生产线上的残次品等。以下是常用的异常检测算法：

基于统计的方法:
- Z-Score: 计算数据点与数据集平均值的偏离程度，使用标准差作为度量。如果一个数据点的Z-Score超过某个阈值（通常是3），则认为它是异常的。
- IQR（四分位距）: 计算数据的第一四分位数（Q1）和第三四分位数（Q3）之间的距离，任何小于Q1-1.5IQR或大于Q3+1.5IQR的值被视为异常。
基于密度的方法:
- 局部异常因子（LOF, Local Outlier Factor）: 通过比较一个数据点与其邻居的密度来识别异常。如果一个点的密度远低于其邻居，则被认为是异常的。
- DBSCAN（Density-Based Spatial Clustering of Applications with Noise）: 一种聚类算法，能够识别出低密度区域的点作为异常点。
基于距离的方法:
- K-最近邻（KNN）: 通过计算一个数据点到其K个最近邻的距离的平均值或加权平均值，如果这个值显著高于其他点，则认为该点是异常的。
基于概率模型的方法:
- 高斯混合模型（GMM）: 利用GMM拟合数据分布，异常点被定义为在模型下概率很低的点。
- 隐马尔可夫模型（HMM）: 对于序列数据，HMM可以用来学习数据的正常行为模式，异常则表现为模型预测概率显著降低的状态。
基于机器学习的方法:
- 孤立森林（Isolation Forest）: 通过构建随机的决策树来“隔离”数据点，异常点更容易被“孤立”，因此通过平均路径长度来评估数据点的异常程度。
- 支持向量机（SVM）: 在异常检测中，可以通过一类SVM（只有一类标签的数据）来构造一个边界，将大部分数据包含在内，超出这个边界的点视为异常。
深度学习方法:
- 自编码器（Autoencoders）: 通过训练一个自编码器来重构输入数据，异常数据往往导致较大的重构误差。
- 生成对抗网络（GANs）: 可以学习数据的正常分布，异常点通过与生成的正常数据对比来识别。

2.2 基于高斯模型的异常检测

高斯模型是一种连续型概率模型，用于表示服从高斯分布（正态分布）的数据。

n维高斯分布：

$f(\textbf{x}|\theta )=\frac{1}{(2\pi)^{n/2}|\sum |^{1/2}}exp[-\frac{1}{2}(\textbf{x}-\mu )^{T}|\sum |^{-1}(\textbf{x}-\mu )]$

上式中， $\theta=(\mu ,\sum )$ 为待估计参数， $\mu$ 是均值， $\sigma ^2$ 是方差，由最大似然估计得到。

n=1时，上式变为一元高斯分布：

$f(x|\theta )=\frac{1}{(2\pi)^{1/2}\sigma }exp[-\frac{1}{2}(x-\mu )^2\sigma ^{-2}]=\frac{1}{\sqrt{2\pi}\sigma }exp[-\frac{(x-\mu )^2}{2\sigma ^{2}}]$

上式中，参数 $\mu$ 和 $\sigma ^2$ 按下式估计：

$\mu_j=\frac{1}{m}\sum_{i=1}^{m}x_j^{(i)}$

$\sigma^2_j=\frac{1}{m}\sum_{i=1}^{m}(x_j^{(i)}-\mu_j)^2$

上式中，j为特征序数，i为特征的数据序数，m为数据总数。

基于高斯模型的异常检测的原理即选定一个适当小的概率值 $p_\varepsilon$ 作为界限，出现概率小于 $p_\varepsilon$ 的数据均为异常数据。如下图所示（以1维为例）：

03 利用异常检测算法检测网络服务器的故障

3.1 问题描述

假设你现在是贝塔科技公司的高级主管，负责公司的服务器运维。今天你抽检了服务器的307份数据，打算采用“传输的数据量 (mb/s，每秒兆字节)”和“每台服务器的响应延迟（ms，毫秒）”两项指标检测网络服务器是否存在故障。

Let's begining!

3.2 算法实现

（1）导包

import numpy as np
import matplotlib.pyplot as plt
from utils import *

%matplotlib inline

（2）导入数据

数据分为训练集和交叉验证集两部分：训练集共307组数据（抽检的数据），每组数据有2个数值，代表2个特征：“传输的数据量”、“服务器的响应延迟”；交叉验证集收集了307组数据（以前保存的数据），每组数据有3个数值，分别为2个特征和1个值，值为0或1：0为正常、1为异常。训练集数据无标签，用于估计参数 $\mu$ 和 $\sigma ^2$ ；交叉验证集数据被标记0/1，用于确定概率界限 $p_{\varepsilon}$ .。

# 导入数据
X_train, X_val, y_val = load_data()

X_train为训练数据集的特征列（307*2），X_val为交叉验证集的特征列（307*2），y_val 为交叉验证集的标签列（307*1）。

（3）参数估计

先定义高斯估计函数：

def estimate_gaussian(X): 

    m, n = X.shape
    mu = np.ones(n)
    var = np.ones(n)
    for i in range(n):
        mu = np.sum(X, axis=0) / m    
        var = np.sum((X - mu) **2, axis=0) / m
        
    return mu, var

然后估计参数：

# 估计每个特征的参数
mu, var = estimate_gaussian(X_train)              

print("Mean of each feature:", mu)
print("Variance of each feature:", var)

运行以上代码，结果如下：

Mean of each feature: [14.11222578 14.99771051]
Variance of each feature: [1.83263141 1.70974533]

现在有了参数 $\mu$ 和 $\sigma ^2$ ，我们可以绘出概率密度分布：

# visualize_fit为自定义绘图函数
#visualize_fit(X_train, mu, var)
visualize_fit(X_val, mu, var)

运行以上代码，结果如下（左为训练集、右为交叉验证集）：

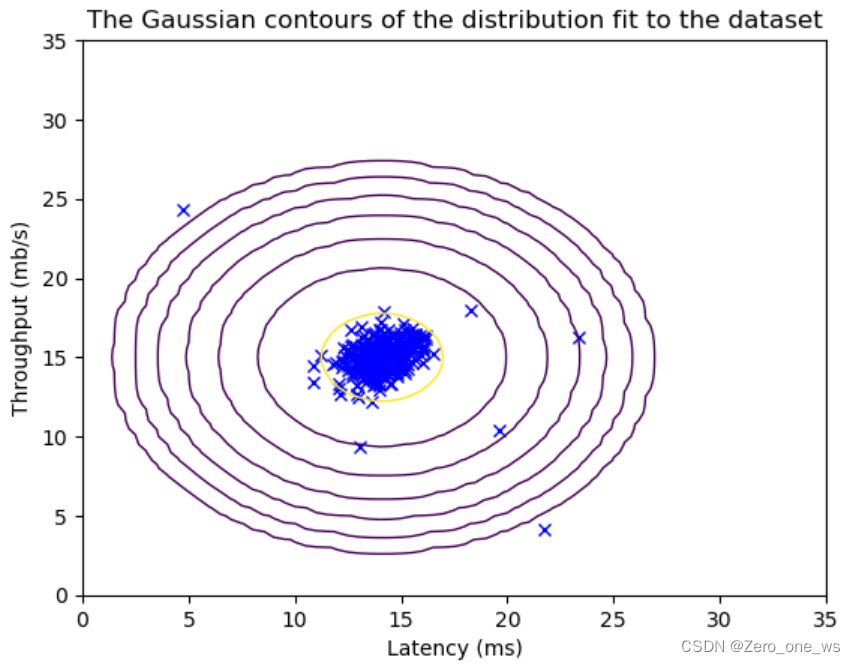
（4）定义概率模型

得到估计参数 $\mu$ 和 $\sigma ^2$ 后，可以利用高斯分布定义概率模型：

def multivariate_gaussian(X, mu, var):
    
    k = len(mu)
    
    if var.ndim == 1:
        var = np.diag(var)
        
    X = X - mu
    p = (2* np.pi)**(-k/2) * np.linalg.det(var)**(-0.5) * \
        np.exp(-0.5 * np.sum(np.matmul(X, np.linalg.pinv(var)) * X, axis=1))
    
    return p

（上面，定义了一个n维高斯分布的概率模型）

（5）确定概率界限

确定概率界限的原则是， $p_{\varepsilon}$ 在合理的取值下，当 $p_a<p_{\varepsilon}$ 时，在交叉验证集中异常点a能被准确识别到。如何保证高精度地识别异常呢？可以采用F1评分标准，取一系列 $p_{\varepsilon}$ 进行计算，谁的F1分数最高就选谁，步骤如下：

首先，给定 $p_{\varepsilon}$ 进行预测，将预测值与实际值进行对比得到4类情况，如下表：

然后，计算两个指标：precision（精度，查准率）和recall（召回率，查全率）：

$prec=\frac{tp}{tp+fp}$

$rec=\frac{tp}{tp+fn}$

precision的含义是异常预测正确的概率有多大，recall的含义是成功找出异常的概率有多大。这两个指标存在这样的问题：当阈值 $p_{\varepsilon}$ 设置为大值时prec增大、rec减小，当阈值 $p_{\varepsilon}$ 设置为小值时prec减小、rec增大。

接下来，计算一个更均衡的指标F1：

$F_1=\frac{2\cdot prec\cdot rec}{prec + rec}$

F1将prec和rec进行了平衡，并且F1数值受二者中较小值控制。

现在，可以定义概率界限计算函数：

def select_threshold(y_val, p_val): 

    best_epsilon = 0
    best_F1 = 0
    F1 = 0
    
    step_size = (max(p_val) - min(p_val)) / 1000
    
    for epsilon in np.arange(min(p_val), max(p_val), step_size):
     
        predictions = p_val < epsilon
        tp = np.sum((predictions == 1) & (y_val == 1))
        fp = np.sum((predictions == 1) & (y_val == 0))
        fn = np.sum((predictions == 0) & (y_val == 1))

        if (tp + fp)  == 0 or (tp + fn) == 0:
            prec = 0
            rec = 0
            F1 = 0
        else:
            prec = tp / (tp + fp)
            rec = tp / (tp + fn)
            F1 = 2 * prec * rec / (prec + rec)
        
        if F1 > best_F1:
            best_F1 = F1
            best_epsilon = epsilon
        
    return best_epsilon, best_F1

然后，执行函数计算：

p_val = multivariate_gaussian(X_val, mu, var)
epsilon, F1 = select_threshold(y_val, p_val)

print('Best epsilon found using cross-validation: %e' % epsilon)
print('Best F1 on Cross Validation Set: %f' % F1)

运行以上代码，结果如下：

Best epsilon found using cross-validation: 8.990853e-05
Best F1 on Cross Validation Set: 0.875000

（6）检测异常，可视化

# 在训练集上找出异常值
outliers = p < epsilon

# 二维图中绘出307组数据
visualize_fit(X_train, mu, var)

# 用红色圆圈标记异常值
plt.plot(X_train[outliers, 0], X_train[outliers, 1], 'ro',
         markersize= 10,markerfacecolor='none', markeredgewidth=2)

运行以上代码，结果如下：

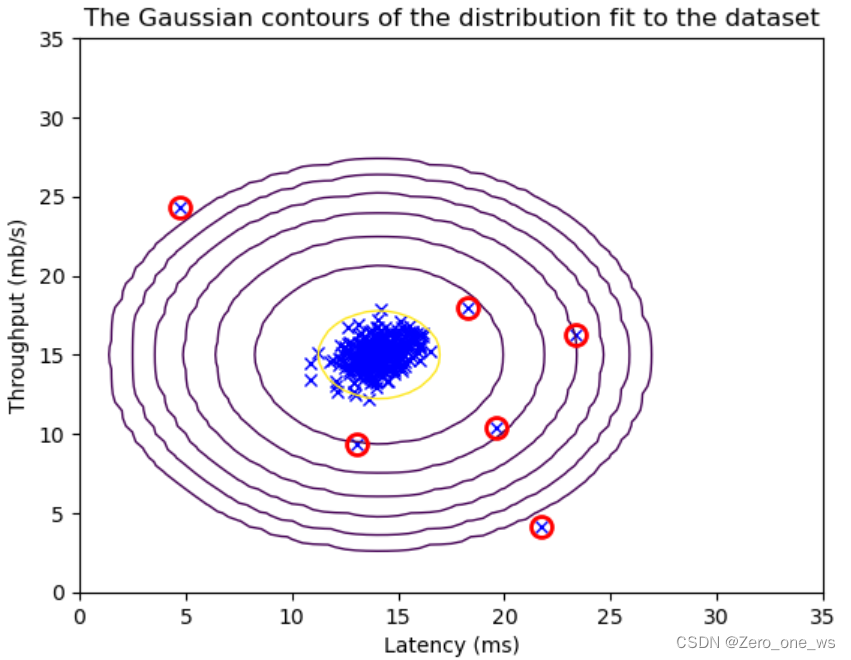
经过一番操作，发现这抽检的307组合数据中有6组异常。

3.3 问题升级

当你检测出异常后，贝塔科技公司的同事们不停欢呼、夸赞你技术高超，希望你再秀一秀高级的。身为主管的你决定再抽检一批数据，以11个特征为依据进行异常检测。

开始吧！

（1）导入数据

# 导入数据
X_train_high, X_val_high, y_val_high = load_data_multi()
# 打印数据信息
print ('The shape of X_train_high is:', X_train_high.shape)
print ('The shape of X_val_high is:', X_val_high.shape)
print ('The shape of y_val_high is: ', y_val_high.shape)

运行以上代码，结果为：

The shape of X_train_high is: (1000, 11)
The shape of X_val_high is: (100, 11)
The shape of y_val_high is:  (100,)

（2）开始检测

# 参数估计
mu_high, var_high = estimate_gaussian(X_train_high)

# 训练集的概率计算
p_high = multivariate_gaussian(X_train_high, mu_high, var_high)

# 交叉验证集的概率计算
p_val_high = multivariate_gaussian(X_val_high, mu_high, var_high)

# 寻找界限
epsilon_high, F1_high = select_threshold(y_val_high, p_val_high)

# 计算异常数量
anomalies = sum(p_high < epsilon_high)

print('Best epsilon found using cross-validation: %e'% epsilon_high)
print('Best F1 on Cross Validation Set:  %f'% F1_high)
print('# Anomalies found: %d'% anomalies)

运行以上代码，结果为：

Best epsilon found using cross-validation: 1.377229e-18
Best F1 on Cross Validation Set:  0.615385
# Anomalies found: 117

04 总结

（1）异常检测算法的交叉验证集数据也是有标记的，但不同于监督学习算法的二分类：异常检测的数据中异常类型较多、但数量较少，分布极为不均。

（2）异常检测的实现算法与维度（特征数）无关，均为4个步骤：参数估计>概率计算>确定阈值>检测异常。