104 二叉树的最大深度

看完题后的思路

后续遍历

1. 深度 f(root)
2. 终止条件 root==null return 0
3. 递归

if root=null
	return 0;
left=f(root.left);
right=f(root.right);
return max(left,right)+1;

思路

节点深度: 该节点到根节点的节点数,某个节点的深度一次就能求出来
节点高度:该节点到叶子节点的最长路径节点数,需要求所有的路径后,找一个最大的

二叉树的最大深度=根节点的高度

方法1 后续遍历
通过求子节点的高度,迭代求根节点的高度=二叉树的最大深度

方法2 前序遍历

通过求每一个节点的深度,找出最大的深度
void f(root,depth)
终止调价 if root==null return
递归
终止条件
maxdepth=max(maxdepth,depth)

 // 104.二叉树的最大深度
    int maxDepth=0;
    public int maxDepth(TreeNode root) {
        maxDepth(root,1);
        return maxDepth;
    }

    public void maxDepth(TreeNode root,int depth) {
        if (root==null){
            return;
        }
        maxDepth= Math.max(maxDepth,depth);
        maxDepth(root.left,depth+1);
        maxDepth(root.right,depth+1);
    }

方法三 迭代
本题使用层序遍历

  public int maxDepth(TreeNode root) {
        if (root==null){
            return 0;
        }
        int res=0;
        ArrayDeque<TreeNode> deque = new ArrayDeque<>();
        deque.offer(root);
        while (!deque.isEmpty()){
            int size = deque.size();
            while (size>0){
                TreeNode poll = deque.poll();
                if (poll.left!=null){
                    deque.offer(poll.left);
                }
                if (poll.right!=null){
                    deque.offer(poll.right);
                }
                size--;
            }
            res++;  // 一层遍历完 ++
        }
        return res;
    }

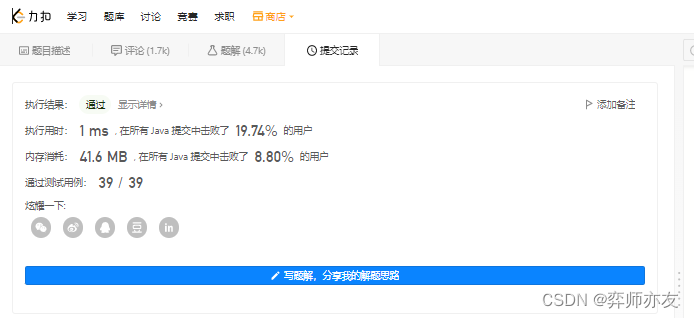
收获

三刷时前序遍历写一遍

559.n叉树的最大深度

看完题后的思路

使用前序遍历

   int nmaxDepth=0;
    public int maxDepth(Node root) {
        maxDepth(root,1);
        return nmaxDepth;
    }
    public void maxDepth(Node root,int depth) {
        if (root==null){
            return;
        }
        nmaxDepth= Math.max(nmaxDepth,depth);
        for (Node child : root.children) {
            maxDepth(child,depth+1);
        }
    }

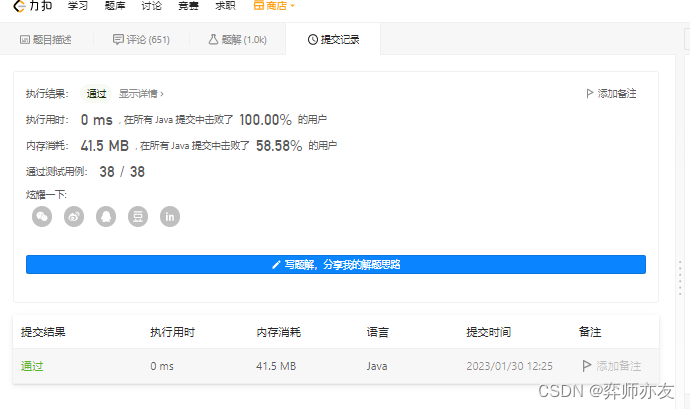
收获

三刷直接过

111.二叉树的最小深度

看完题后的思路

方式1: 使用前序 统计所有叶子节点的深度,找出最小的

  int minDepth=111111111;
    public int minDepth(TreeNode root) {
          if (root==null){
            return 0;
        }
        minDepth(root,1);
        return minDepth;
    }
    public void minDepth(TreeNode root,int depth) {
        if (root==null){
            return;
        }
        if (root.left==null&&root.right==null){
            minDepth= Math.min(minDepth,depth);
        }
        minDepth(root.left,depth+1);
        minDepth(root.right,depth+1);
    }

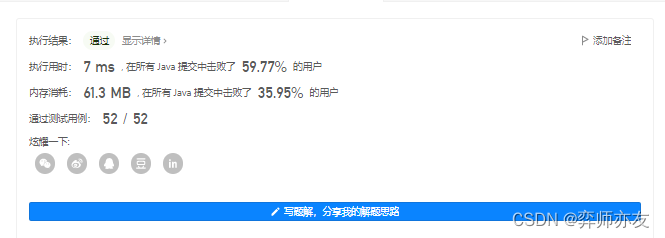
方法2 迭代+层序
当碰到某个叶子节点就停止迭代

 public int minDepth(TreeNode root) {
        if (root==null){
            return 0;
        }
        int res=0;
        ArrayDeque<TreeNode> deque = new ArrayDeque<>();
        deque.offer(root);
        while (!deque.isEmpty()){
            int size = deque.size();
            while (size>0){
                TreeNode poll = deque.poll();
                if (poll.left==null&& poll.right==null){
                    return res+1;
                }
                if (poll.left!=null){
                    deque.offer(poll.left);
                }
                if (poll.right!=null){
                    deque.offer(poll.right);
                }
                size--;
            }
            res++;  // 一层遍历完 ++
        }
        return res;
    }

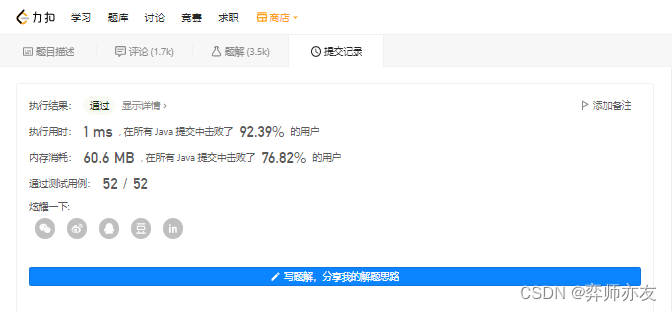
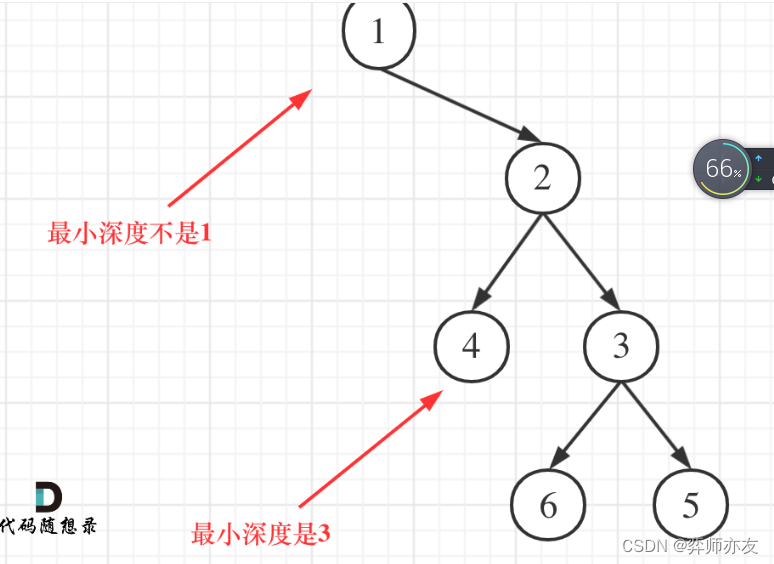
方法3 后序
根节点的最小高度是二叉树的最小深度吗？

后续遍历

1. 深度 f(root)
2. 终止条件 root==null return 0
3. 递归

if root=null
	return 0;
left=f(root.left);
right=f(root.right);
if（left==0&&right==0）
	return 1
if（left==0||right==0）{
	return max(left,right)+1;
}
// 全不为0

return min(left,right)+1;


return max(left,right)+1;

代码

 public int minDepth(TreeNode root) {
        if (root == null) {
            return 0;
        }
        int left = minDepth(root.left);
        int right = minDepth(root.right);
        if (left==0&&right==0){
            return 1;
        }
        // 一个为0
        if (left==0||right==0){
            return Math.max(left,right)+1;
        }
        // 全不为0
        
        return Math.min(left,right)+1;
    }

收获

三刷前序 后续都看

222.完全二叉树的节点个数

看完题后的思路

1. 个数 f(root)
2. 递归终止
   if(root==null)
   return 0
3. 递归

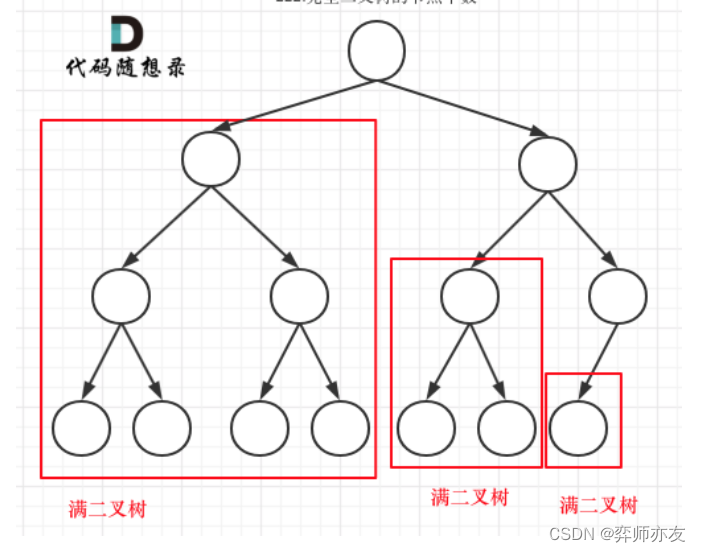
   if(root==null)
   return 0
   if 左子树是完全二叉树
   直接返回左子树的个数
   否则 递归左子树
   if 右子树是完全二叉树
   直接返回右子树个数
   否则 递归右子树
   

return 左+右+1
```

代码

//222. 完全二叉树的节点个数
    public int countNodes(TreeNode root) {
        if (root==null){
            return 0;
        }
        int left,right;
        int leftDepth = isFullTree(root.left);
        int rightDepth = isFullTree(root.right);
        if (leftDepth!=-1){
            left=(int) Math.pow(2,leftDepth)-1;
        }else {
            left=countNodes(root.left);
        }
        
        if (rightDepth!=-1){
            right=(int) Math.pow(2,rightDepth)-1;
        }else {
            right=countNodes(root.right);
        }
        return left+right+1;
    }
    public int isFullTree(TreeNode root){
        if (root==null){
            return 0;
        }
        TreeNode left=root,right=root;
        int depth=0;
        while (left!=null&&right!=null){
            left=left.left;
            right=right.right;
            depth++;
        }
        if (left!=null||right!=null){
            return -1;
        }
        return depth;
    }

复杂度

收获

三刷看一遍