目录
1.程序功能描述
2.测试软件版本以及运行结果展示
3.核心程序
4.本算法原理
4.1NURBS曲线基础
4.2 数据拟合原理
5.完整程序
1.程序功能描述
基于NURBS曲线的数据拟合算法,非均匀有理B样条(Non-Uniform Rational B-Splines,简称NURBS)曲线是一种强大的数学工具,广泛应用于计算机图形学、CAD/CAM系统、几何建模和数据拟合等领域。NURBS曲线通过控制顶点和权重,能够精确地表示复杂的曲线和曲面形状,特别适合于对真实世界对象的建模和数据点的光滑拟合。
2.测试软件版本以及运行结果展示
MATLAB2022A版本运行
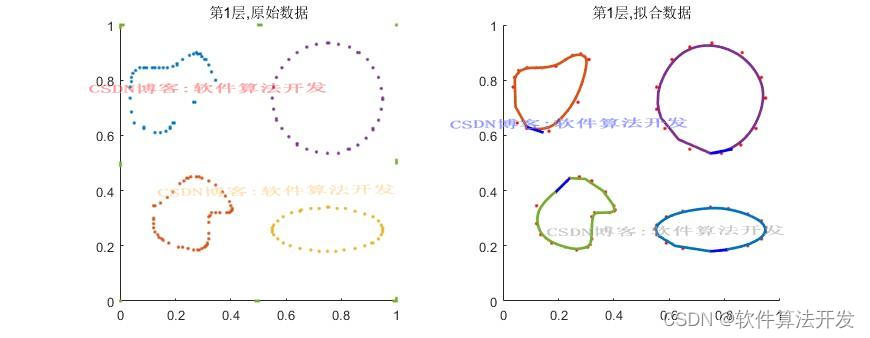
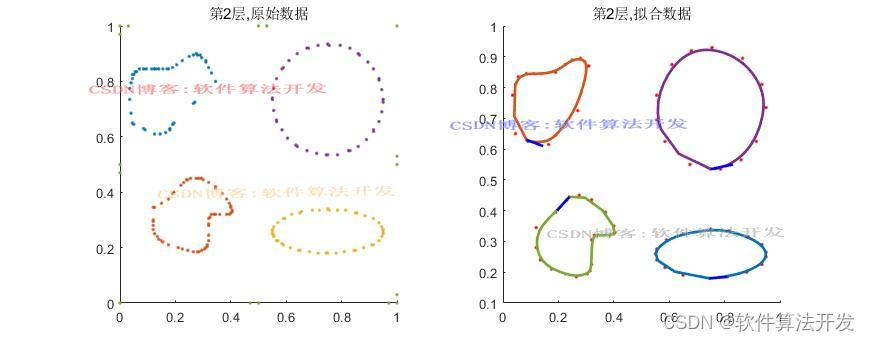
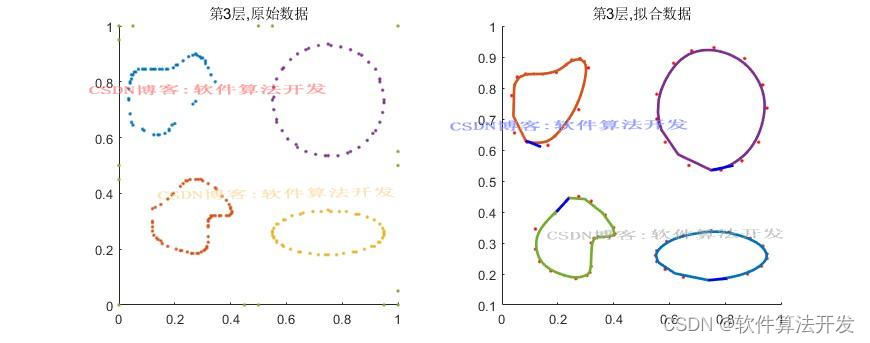
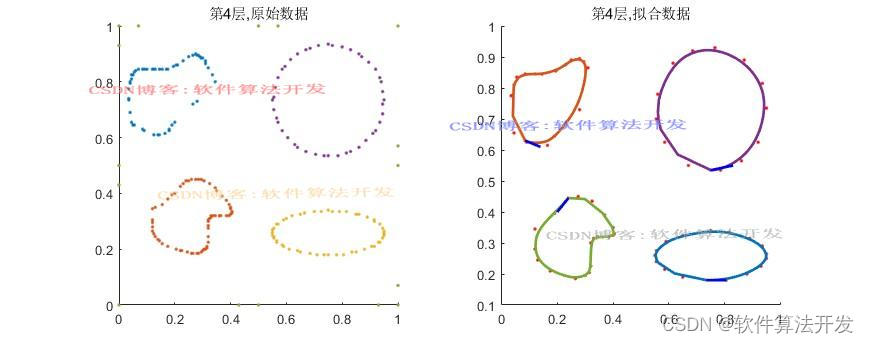
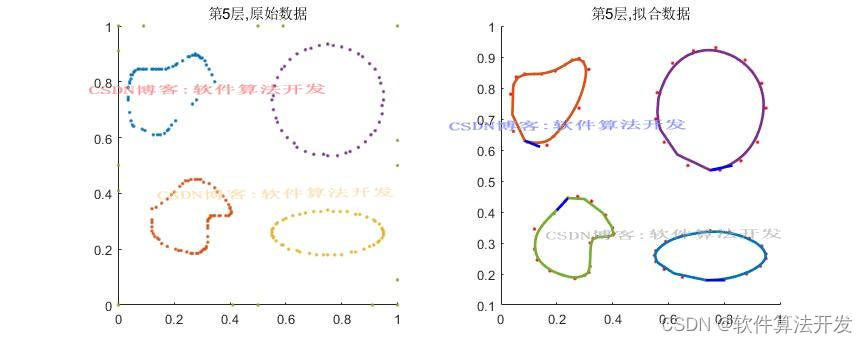

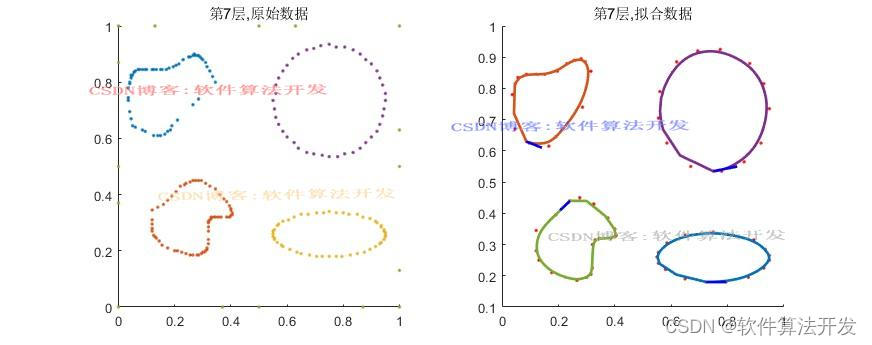
(完整程序运行后无水印)
3.核心程序
......................................................
%拟合前路径段数
layer2(i).outline(j).qlj_number = length(points);
%拟合前最大路径长度
for jj = 1:length(points)-1
dist1(jj) = sqrt((points(jj,1) - points(jj+1,1))^2 + (points(jj,2) - points(jj+1,2))^2);
end
layer2(i).outline(j).qlj_maxlen = max(dist1);
%拟合前平均路径长度
layer2(i).outline(j).qlj_meanlen= mean(dist1);
%拟合前最小路径长度
layer2(i).outline(j).qlj_minlen = min(dist1);
%拟合前最大拟合误差
layer2(i).outline(j).qlj_error = 0;
%拟合后路径段数
layer2(i).outline(j).hlj_number = NUM;
%拟合后最大路径长度
for jj = 1:length(points2)-1
dist2(jj) = sqrt((points2(jj,1) - points2(jj+1,1))^2 + (points2(jj,2) - points2(jj+1,2))^2);
end
layer2(i).outline(j).hlj_maxlen = max(dist1);
%拟合后平均路径长度
layer2(i).outline(j).hlj_meanlen= mean(dist1);
%拟合后最小路径长度
layer2(i).outline(j).hlj_minlen = min(dist1);
%拟合后最大拟合误差
layer2(i).outline(j).hlj_error = max(miss);
end
end
axis square;
end
16_039m4.本算法原理
非均匀有理B样条(Non-Uniform Rational B-Splines,简称NURBS)曲线是一种强大的数学工具,广泛应用于计算机图形学、CAD/CAM系统、几何建模和数据拟合等领域。NURBS曲线通过控制顶点和权重,能够精确地表示复杂的曲线和曲面形状,特别适合于对真实世界对象的建模和数据点的光滑拟合。
4.1NURBS曲线基础
NURBS曲线是一类特殊的有理B样条曲线,它结合了非均匀(控制点具有不同的参数间隔)和有理(控制点带有权重)的特点。NURBS曲线的数学表达式为:

4.2 数据拟合原理
数据拟合是指通过调整NURBS曲线的控制顶点位置、权重及可能的结点分布,使得曲线尽可能接近一组已知数据点。这一过程可以通过最小化某种误差度量(如均方误差)来实现,具体步骤如下:
1.初始化:确定NURBS曲线的阶数p、控制顶点数n以及结点分布。初始控制顶点可以简单地设置为数据点的某个子集或通过某种插值方法初步获得。
2.误差评估:定义误差函数E来衡量曲线与数据点集的偏差,例如:
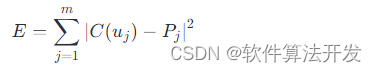
其中,m是数据点的数量,Pj是第j个数据点的位置,uj是对应数据点在参数空间的参数值。
3.参数优化:通过梯度下降、共轭梯度法、遗传算法等优化技术,调整控制顶点位置、权重及结点分布,以最小化误差函数E。
4.迭代收敛:重复步骤2和3,直到误差函数下降到预设阈值或迭代次数达到上限。
在拟合过程中,权重wi的调整尤为关键,因为它不仅影响曲线的形状,还能通过放大或缩小控制顶点的作用来适应数据点的分布。一种策略是根据数据点的密度或拟合误差动态调整权重,使得曲线在数据密集区域更加平滑,在数据稀疏区域保持对数据点的追踪。
5.完整程序
VVV