目录
- 1.算法原理
- 2.改进点
- 3.结果展示
- 4.参考文献
- 5.代码获取
1.算法原理
SCI二区|鲸鱼优化算法(WOA)原理及实现【附完整Matlab代码】
2.改进点
混沌反向学习策略
将混沌映射和反向学习策略结合,形成混沌反向学习方法,通过该方
法生成鲸鱼算法的初始种群。混沌序列采用 Tent 混沌映射:
x
i
+
1
=
{
δ
x
i
0
<
x
i
<
0.5
δ
(
1
−
x
i
)
0.5
<
x
i
<
1
(1)
x_{i+1}=\begin{cases}\delta x_i&\quad0<x_i<0.5\\\delta(1-x_i)&\quad0.5<x_i<1\end{cases}\tag{1}
xi+1={δxiδ(1−xi)0<xi<0.50.5<xi<1(1)
反向学习是一种扰动手段,其主要原理是通过对目标空间中已知解的反向学习,得到该解在空间中的反向解:
x
′
=
r
(
x
max
−
x
min
)
−
x
(2)
x'=r(x_{\max}-x_{\min})-x\tag{2}
x′=r(xmax−xmin)−x(2)
将混沌生成种群和反向学习种群混合,取适应度前1/2作为新种群。
自适应收敛因子策略
在鲸鱼算法中,收敛因子a从2线性递减到 0,对适应度不同的鲸鱼个体,其包围步长的计算方法是一致的,没有反映出鲸鱼个体间的差异。因此,采用自适应收敛因子:
a
=
2
−
(
2
−
2
⋅
r
a
n
k
i
N
)
⋅
sin
(
t
2
⋅
T
max
π
)
(3)
a=2-(2-2\cdot\frac{rank_i}N)\cdot\sin(\frac t{2\cdot T_{\max}}\pi)\tag{3}
a=2−(2−2⋅Nranki)⋅sin(2⋅Tmaxtπ)(3)
其中,ranki 为个体的适应度值在种群中的排名。
随机差分策略
为避免鲸鱼算法陷入局部最优,采用随机差分策略进行扰动,采用贪心策略选择解:
X
(
t
+
1
)
=
r
1
(
X
′
(
t
)
−
X
(
t
)
)
−
r
2
(
X
∗
(
t
)
−
X
(
t
)
)
(4)
X(t+1)=r_1(X'(t)-X(t))-r_2(X^*(t)-X(t))\tag{4}
X(t+1)=r1(X′(t)−X(t))−r2(X∗(t)−X(t))(4)
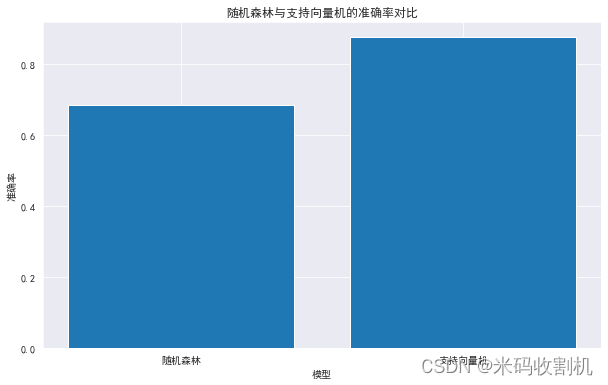
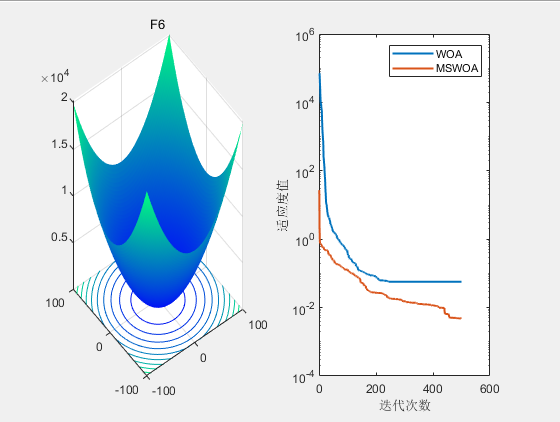
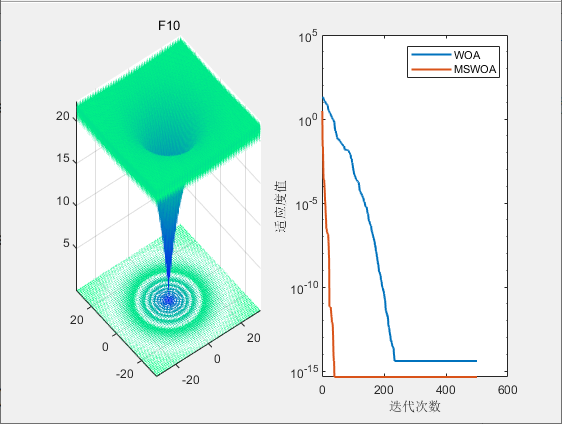
3.结果展示


4.参考文献
[1] 吕嘉婧,李磊.一种基于多策略改进的鲸鱼算法[J].信息技术与信息化,2024,(02):39-42.