一、概念
给定一张有向图,如果存在一个环,环上各边权值之和是负数,则称这个环为负环。
判断方式:bellman-ford算法和spfa算法。+抽屉原理
这里只介绍spfa。设立cnt数组表示从1到x的最短路径包含的边数,如果cnt[i]大于等于n,则存在负环。
二、例题
904. 虫洞

 虫洞是负边,存在负环则true。
虫洞是负边,存在负环则true。
#include<iostream>
#include<algorithm>
#include<cstring>
#include<queue>
using namespace std;
const int N =510,M=5210;
int f,n,m1,m2;
int dist[N];
int h[N],e[M],ne[M],w[M],idx;
bool st[N];
int cnt[N];
int q[N];
void add(int a,int b,int c)
{
e[idx]=b,w[idx]=c,ne[idx]=h[a],h[a]=idx++;
}
bool spfa()
{
memset(dist,0,sizeof dist);
memset(cnt, 0, sizeof cnt);
queue<int> q;
for(int i=1;i<=n;i++)
{
q.push(i);
st[i]=true;
}
while(q.size())
{
int t=q.front();
q.pop();
st[t]=false;
for(int i=h[t];~i;i=ne[i])
{
int j=e[i];
if(dist[j]>dist[t]+w[i])
{
dist[j]=dist[t]+w[i];
cnt[j]=cnt[t]+1;
if(cnt[j]>=n) return true;
if(!st[j])
{
st[j]=true;
q.push(j);
}
}
}
}
return false;
}
int main()
{
cin>>f;
while(f--)
{
cin>>n>>m1>>m2;
memset(h,-1,sizeof h);
idx=0;
for(int i=0;i<m1;i++)
{
int a,b,c;
cin>>a>>b>>c;
add(a,b,c),add(b,a,c);
}
for(int i=0;i<m2;i++)
{
int a,b,c;
cin>>a>>b>>c;
add(a,b,-c);
}
if(spfa()) puts("YES");
else puts("NO");
}
return 0;
}
作者:yankai
链接:https://www.acwing.com/activity/content/code/content/4455339/
来源:AcWing
著作权归作者所有。商业转载请联系作者获得授权,非商业转载请注明出处。361. 观光奶牛

这个和01分数规划有关,涉及01分数规划,一般会用二分。
设二分答案为mid:
1.如果图中存在一个环,若,则说明
即本题所求的最大值大于mid
2如果对任意的环,都大于等于0,则说明最大值小于等于mid。
因此可以二分,并且我们发现(1)中的环,实际上可以替代为:没有点权,边权e(x,y)的权值是mid*w(e)-w(x),即本来的边权乘以mid再减去入点的权值。的这样一个环。因此可以构建一个新图。
(1)中的条件变为,这样的新图有负环。
因此二分求解答案即可。
#include<iostream>
#include<algorithm>
#include<cstring>
#include<queue>
using namespace std;
const int N =1010,M=5010;
int n,m;
int wf[N];
int h[N],e[M],ne[M],wt[M],idx;
bool st[N];
int cnt[N];
double dist[N];
int q[N];
void add(int a,int b,int c)
{
e[idx]=b,wt[idx]=c,ne[idx]=h[a],h[a]=idx++;
}
bool check(double mid)
{
memset(dist,0,sizeof dist);
memset(cnt,0,sizeof cnt);
memset(st,0,sizeof st);
queue<int> q;
for(int i=1;i<=n;i++)
{
st[i]=true;
q.push(i);
}
while(q.size())
{
int t=q.front();
q.pop();
st[t]=false;
for(int i=h[t];i!=-1;i=ne[i])
{
int j=e[i];
if(dist[j]>dist[t]+mid*wt[i]-wf[t])
{
dist[j]=dist[t]+mid*wt[i]-wf[t];
cnt[j]=cnt[t]+1;
if(cnt[j]>=n) return true;
if(!st[j])
{
st[j]=true;
q.push(j);
}
}
}
}
return false;
}
int main()
{
cin>>n>>m;
for(int i=1;i<=n;i++) cin>>wf[i];
memset(h,-1,sizeof h);
for(int i=0;i<m;i++)
{
int a,b,c;
cin>>a>>b>>c;
add(a,b,c);
}
double l=0,r=1e6;
while(r-l>1e-4)
{
double mid=(l+r)/2;
if(check(mid)) l=mid;
else r=mid;
}
printf("%.2lf",l);
return 0;
}
作者:yankai
链接:https://www.acwing.com/activity/content/code/content/4455633/
来源:AcWing
著作权归作者所有。商业转载请联系作者获得授权,非商业转载请注明出处。1165. 单词环
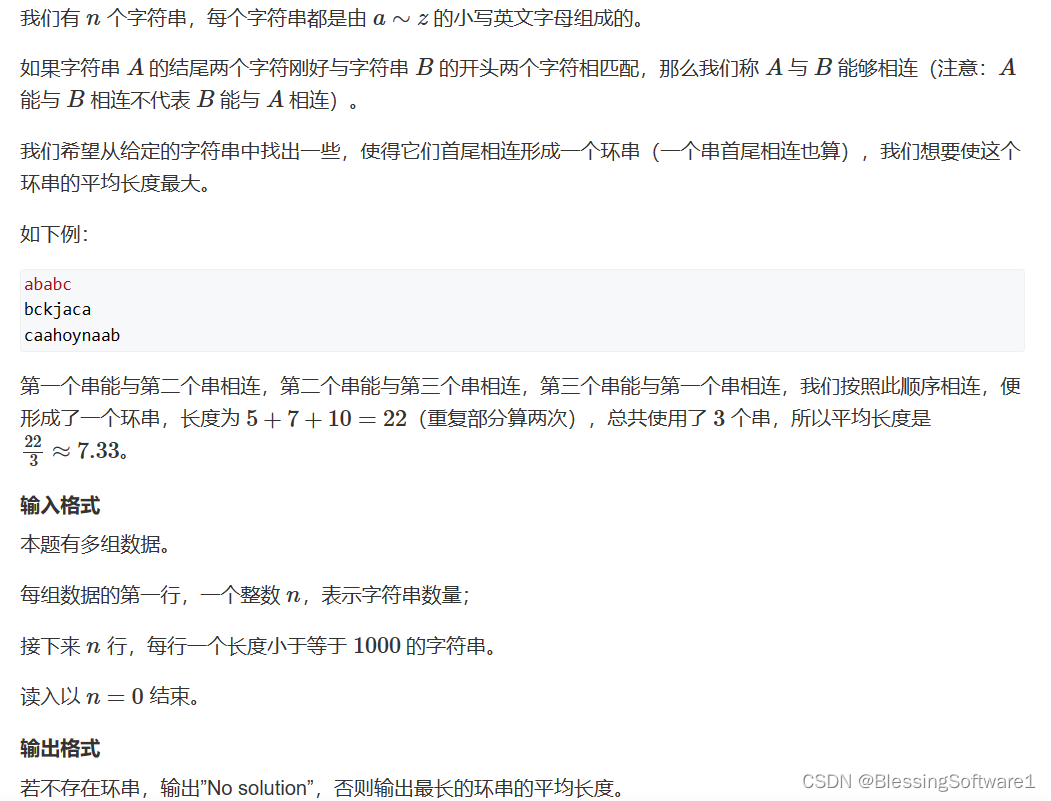
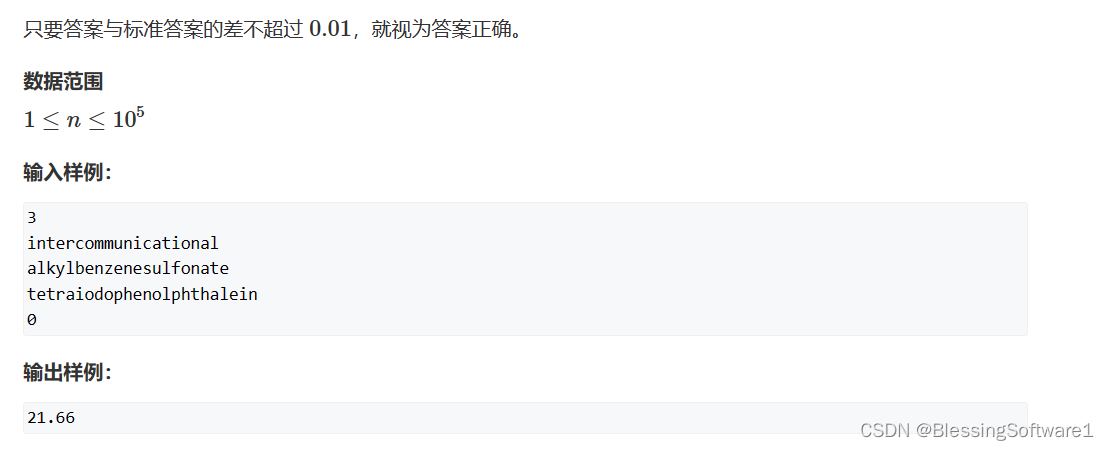
分析:
- 建图:最直观的建图方式,是把每个单词看做节点,然后连接可接龙的单词。但是这样最多有1e5个点,有1e10条边,存不下。因此要换方法。考虑一个对偶的建图方式,将每一个单词看作一条边,其开头两个字符和结尾两个字符为它两边的点。这样建图的话,节点数就缩小到了676个(26∗26)边数为1e5条。
- 01分数规划:我们要求
=k的最大值,设二分答案mid。当k>mid时:
,因此我们把边权设置为len[i]−mid。
- 优化:spfa求负环时,可能一直跑不出结果。可以采取一种比较取巧的方法:当求最长路时,经过的点大于某一个数时,我们就可以武断地认为当前图中存在一个正环.
#include<iostream>
#include<algorithm>
#include<cstring>
#include<queue>
using namespace std;
const int N =700,M=100010;
int n;
double dist[N];
int cnt[N];
int h[N],e[M],ne[M],w[M],idx;
bool st[N];
void add(int a,int b,int c)
{
e[idx]=b,w[idx]=c,ne[idx]=h[a],h[a]=idx++;
}
bool check(double mid)
{
queue<int> q;
memset(dist,0,sizeof dist);
memset(cnt,0,sizeof cnt);
memset(st,0,sizeof st);
for(int i=0;i<676;i++)
{
st[i]=true;
q.push(i);
}
int count=0;
while(q.size())
{
int t=q.front();
q.pop();
st[t]=false;
for(int i=h[t];i!=-1;i=ne[i])
{
int j=e[i];
if(dist[j]>dist[t]+mid-w[i])
{
dist[j]=dist[t]+mid-w[i];
if(++count>10000) return true;
cnt[j]=cnt[t]+1;
if(cnt[j]>=N) return true;
if(!st[j])
{
st[j]=true;
q.push(j);
}
}
}
}
return false;
}
int main()
{
char str[1010];
while(cin>>n,n)
{
memset(h,-1,sizeof h);
idx=0;
for(int i=0;i<n;i++)
{
cin>>str;
int len=strlen(str);
if(len>=2)
{
int left=(str[0] - 'a') * 26 + str[1] - 'a';
int right = (str[len - 2] - 'a') * 26 + str[len - 1] - 'a';
add(left,right,len);
}
}
if(!check(0)) puts("No solution");
else
{
double l=0,r=1010;
while(r-l>1e-5)
{
double mid=(l+r)/2;
if(check(mid)) l=mid;
else r=mid;
}
printf("%.2lf\n",r);
}
}
return 0;
}
作者:yankai
链接:https://www.acwing.com/activity/content/code/content/4455934/
来源:AcWing
著作权归作者所有。商业转载请联系作者获得授权,非商业转载请注明出处。三、差分约束
差分约束就是一组N元一次不等式。给出了多个约束条件形如:。我们要解决的问题就是求出一组X,使得所有约束条件得到满足。
我们可以把看做 j 节点向 i 节点连一条长度为ck的有向边。
则如果a1 a2....an是一组解,则对任意的常数delta,a+delta也是一组解。所以不妨先求一组负数解。假设所有ai小于等于0。我们再增加一个超级原点a0=0,则多了N个形如的约束条件。即我们把0号点向所有点连一条长度为0的边。
在我们建的图上跑最短路,如果存在负环,则说明有ai<ai,这是不可能满足的,所以差分系统无解,否则,ai=dist[i]就是一组解。
如果约束条件不等号反向,我们仍然可以不改变图,只不过改为计算单源最长路,如果有正环则无解。

参考:AcWing 1169. 糖果 - AcWing
AcWing 1169. 糖果 - AcWing
也就是说,如果是求最小值,则求最长路。求最大值,则求最短路。
四、例题
1169. 糖果

注意超级原点。因此本题求最小值,跑最长路判断即可,判断有无正环
#include<iostream>
#include<algorithm>
#include<cstring>
#include<stack>
using namespace std;
const int N =1e5+10,M=3e5+10;
int n,m;
int h[N],e[M],ne[M],w[M],idx;
long long dist[N];
bool st[N];
int cnt[N];
void add(int a,int b,int c)
{
e[idx]=b,w[idx]=c,ne[idx]=h[a],h[a]=idx++;
}
int spfa()
{
memset(dist,-0x3f,sizeof dist);
dist[0]=0;
stack<int> q;
q.push(0);
st[0]=true;
while(q.size())
{
int t=q.top();
q.pop();
st[t]=false;
for(int i=h[t];~i;i=ne[i])
{
int j=e[i];
if(dist[j]<dist[t]+w[i])
{
dist[j]=dist[t]+w[i];
cnt[j]=cnt[t]+1;
if(cnt[j]>=n+1) return false;
if(!st[j])
{
q.push(j);
st[j]=true;
}
}
}
}
return true;
}
int main()
{
cin>>n>>m;
memset(h,-1,sizeof h);
for(int i=0;i<m;i++)
{
int a,b,x;
cin>>x>>a>>b;
if(x==1) add(a,b,0),add(b,a,0);
else if(x==2) add(a,b,1);
else if(x==3) add(b,a,0);
else if(x==4) add(b,a,1);
else add(a,b,0);
}
for(int i=1;i<=n;i++) add(0,i,1);
if(!spfa()) cout<<"-1";
else
{
long long res=0;
for(int i=1;i<=n;i++) res+=dist[i];
cout<<res;
}
}
作者:yankai
链接:https://www.acwing.com/activity/content/code/content/4482434/
来源:AcWing
著作权归作者所有。商业转载请联系作者获得授权,非商业转载请注明出处。362. 区间(前缀和)

AcWing 362. 区间 - AcWing
#include<iostream>
#include<algorithm>
#include<cstring>
#include<queue>
using namespace std;
const int N =5e4+10,M=2e5;
int n;
int h[N],e[M],ne[M],w[M],idx;
int dist[N];
bool st[N];
void add(int a,int b,int c)
{
e[idx]=b,w[idx]=c,ne[idx]=h[a],h[a]=idx++;
}
void spfa()
{
memset(dist,-0x3f,sizeof dist);
queue<int> q;
dist[0]=0;
q.push(0);
st[0]=true;
while(q.size())
{
int t=q.front();
q.pop();
st[t]=false;
for(int i=h[t];~i;i=ne[i])
{
int j=e[i];
if(dist[j]<dist[t]+w[i])
{
dist[j]=dist[t]+w[i];
if(!st[j])
{
q.push(j);
st[j]=true;
}
}
}
}
}
int main()
{
cin>>n;
memset(h,-1,sizeof h);
for(int i=1;i<N;i++)
{
add(i,i-1,-1);
add(i-1,i,0);
}
for(int i=0;i<n;i++)
{
int a,b,c;
cin>>a>>b>>c;
a++,b++;
add(a-1,b,c);
}
spfa();
cout<<dist[50001];
}
1170. 排队布局

无穷即判断1号点和n号点有无约束关系即,即连不连通。

#include<iostream>
#include<algorithm>
#include<cstring>
#include<queue>
using namespace std;
const int N =1010,M=10000+10000+1010,INF=0x3f3f3f3f;
int n,m1,m2;
int dist[N];
bool st[N];
int h[N],e[M],ne[M],w[M],idx;
int cnt[N];
void add(int a,int b,int c)
{
e[idx]=b,w[idx]=c,ne[idx]=h[a],h[a]=idx++;
}
bool spfa(int size)
{
memset(dist,0x3f,sizeof dist);
memset(st,0,sizeof st);
memset(cnt,0,sizeof cnt);
queue<int> q;
for(int i=1;i<=size;i++)
{
q.push(i);
st[i]=true;
dist[i]=0;
}
while(q.size())
{
int t=q.front();
q.pop();
st[t]=false;
for(int i=h[t];i!=-1;i=ne[i])
{
int j=e[i];
if(dist[j]>dist[t]+w[i])
{
dist[j]=dist[t]+w[i];
cnt[j]=cnt[t]+1;
if(cnt[j]>=n) return true;
if(!st[j])
{
q.push(j);
st[j]=true;
}
}
}
}
return false;
}
int main()
{
cin>>n>>m1>>m2;
memset(h,-1,sizeof h);
for(int i=1;i<n;i++) add(i+1,i,0);
for(int i=0;i<m1;i++)
{
int a,b,c;
cin>>a>>b>>c;
if(a>b) swap(a,b);
add(a,b,c);
}
for(int i=0;i<m2;i++)
{
int a,b,c;
cin>>a>>b>>c;
if(a>b) swap(a,b);
add(b,a,-c);
}
if(spfa(n)) puts("-1");//出现矛盾 有负环
else
{
spfa(1);
if(dist[n]==INF) puts("-2");
else cout<<dist[n];
}
return 0;
}
作者:yankai
链接:https://www.acwing.com/activity/content/code/content/4494625/
来源:AcWing
著作权归作者所有。商业转载请联系作者获得授权,非商业转载请注明出处。393. 雇佣收银员