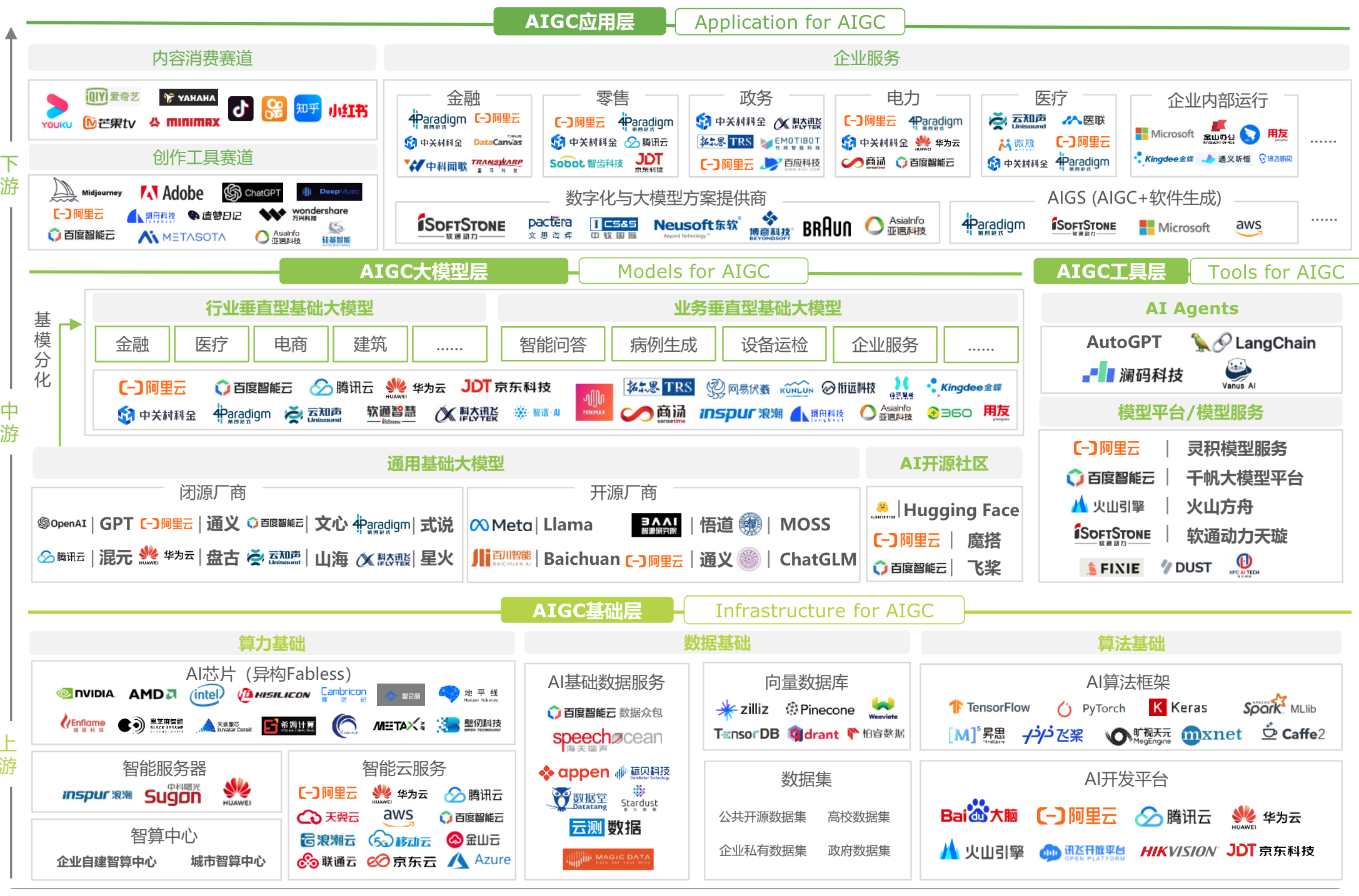
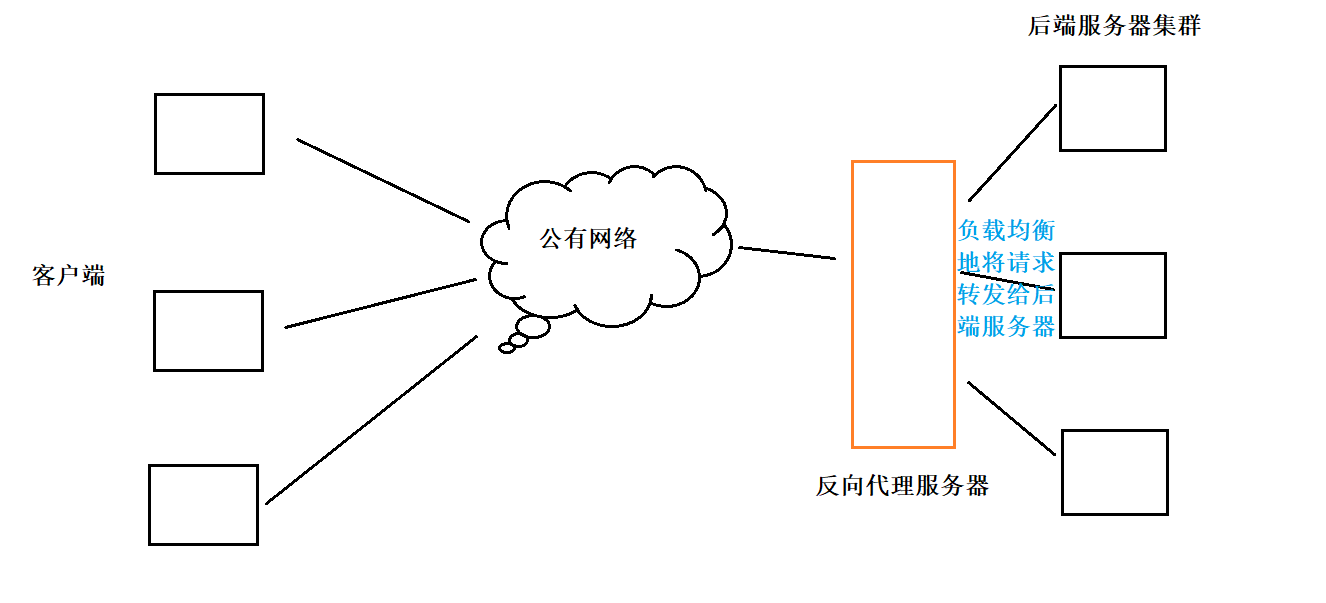
要计算一个类对象的大小要先明白一个问题：类中既可以有成员变量，又可以有成员函数，那么一个类的对象中包含了什么？

下面来看一段代码：

// 类中既有成员变量，又有成员函数
class A1 {
public:
	void f1() {}
private:
	int _a;
};
// 类中仅有成员函数
class A2 {
public:
	void f2() {}
};
// 类中仅有成员变量
class A3
{
public:
	int _a;
};
int main()
{
	cout << sizeof(A1) << endl;// 4
	cout << sizeof(A2) << endl;// 1
	cout << sizeof(A3) << endl;// 4
}

通过代码演示实际上我们可以发现类中的成员函数不影响类的大小。实际上由于同一个类的每个对象中只有变量不一样，而函数代码都是一样的，所以没有必要每个对象都存一份函数代码。代码只保存一份，在对象中保存存放代码的地址。

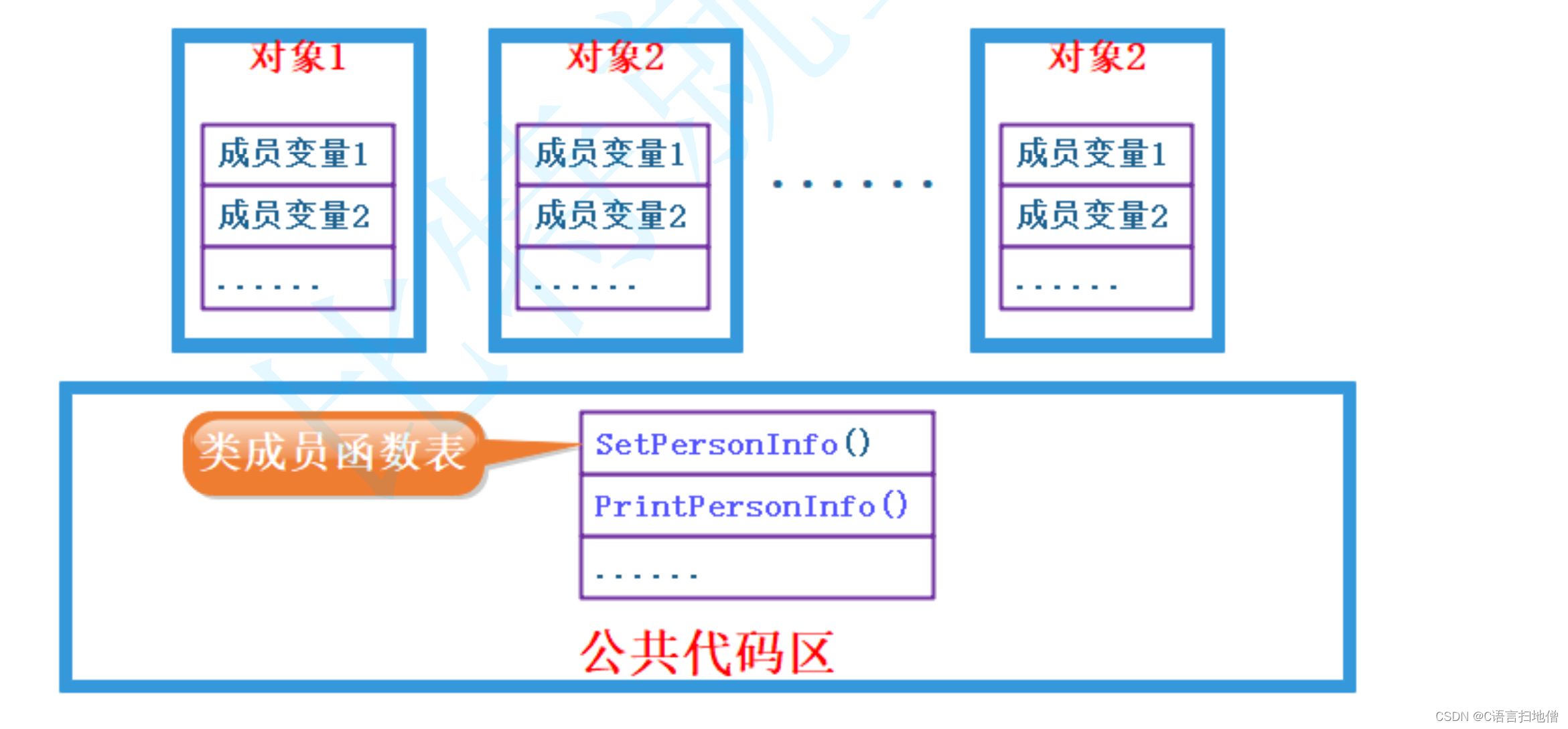
结论：一个类的大小，实际就是该类中”成员变量”之和，当然要注意内存对齐。

结构体内存对齐规则：
1. 第一个成员在与结构体偏移量为0的地址处。
2. 其他成员变量要对齐到某个数字（对齐数）的整数倍的地址处。
注意：对齐数 = 编译器默认的一个对齐数 与 该成员大小的较小值。
VS中默认的对齐数为8
3. 结构体总大小为：最大对齐数（所有变量类型最大者与默认对齐参数取最小）的整数倍。
4. 如果嵌套了结构体的情况，嵌套的结构体对齐到自己的最大对齐数的整数倍处，结构体的整体大小就是所有最大对齐数（含嵌套结构体的对齐数）的整数倍。