目录
一、图的基本概念
1.1图的种类
1.2顶点的度、入度和出度
1.3边的权和网
1.4路径、路径长度和回路
二、图的存储结构
2.1邻接矩阵法
2.2邻接表法
2.3十字链表
2.4邻接多重表
三、图的遍历
3.1广度优先搜索
3.2深度优先搜索
四、图的应用
4.1最小生成树
4.1.1普里姆算法
4.1.2克鲁斯卡尔算法
4.2最短路径
4.2.1迪杰斯特拉算法
4.3拓扑排序
4.4关键路径
一、图的基本概念
1.1图的种类
①有向图:v,w表示顶点,顶点间的边是有方向的。
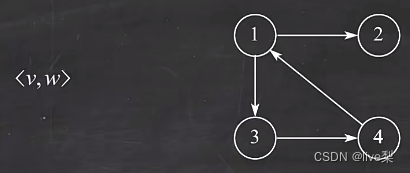
②无向图:v,w表示顶点,顶点间的边没有方向。

③简单图:不存在重复边,不存在顶点到自身的边。
④多重图:存在重复边,存在顶点到自身的边。
⑤完全图:(简单完全图)
对于无向图,任意两个顶点之间都存在边,边的条数:(n*(n-1))/2
对于有向图,任意两个顶点之间都存在方向相反的两条弧,边的条数:n*(n-1)
⑥
子图: 顶点和边是另一个图的子集的图。
 、
、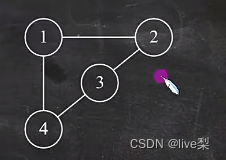
第二个图的顶点和边都是第一个图的子集,所以图2是图1的子图。
生成子图:顶点相等,边是另一个图的子集的图。
 、
、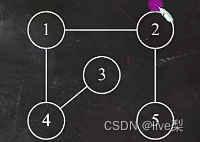
第二个图的顶点和第一个图相等,边是它的子集,所以图2是图1的生成子图。
⑦
连通图:图中任意两个顶点都是连通的。

极小连通子图:既要保持图连通又要使得边数最少的子图。

⑧生成树:包含图中全部顶点的一个极小连通子图。(边数=顶点数-1)
 、
、
图2是图1的生成树。
1.2顶点的度、入度和出度
度:一个顶点连接的边数
①对于无向图:其全部顶点的度的和等于边数的2倍
②对于有向图:
·入度是以顶点v为终点的有向边的数目,出度是以顶点v为起点的有向边的数目;
·顶点的度=入度和出度之和;
·有向图的全部顶点的入度之和与出度之和=,并且=边数。
1.3边的权和网
权:边上带有数值,这样的图称为带权图或网
1.4路径、路径长度和回路
路径:顶点到另一个顶点的路线
路径长度:顶点到另一个顶点的距离
回路:从某一个顶点出发,最后又回到这个顶点
二、图的存储结构
2.1邻接矩阵法
行列与顶点有关,与边无关
①对于无向图:A[i][j]=1,(vi,vj)存在;A[i][j]=0,(vi,vj)不存在 (对称矩阵)

②对于有向图:A[i][j]=1,(vi,vj)存在;A[i][j]=0,(vi,vj)不存在

③对于带权图:A[i][j]=权值,(vi,vj)存在;A[i][j]=0或无穷大,(vi,vj)不存在
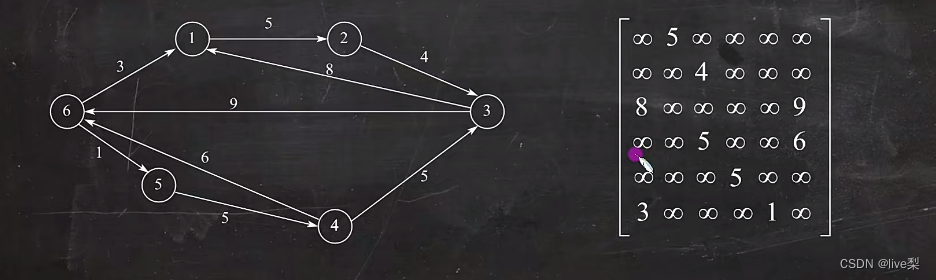
问:
①n个顶点的无向连通图用邻接矩阵表示时,该矩阵至少有2(n-1)个非零元素。
(有n-1条边,每条边表示两次)
②带权有向图G用邻接矩阵A存储,则顶点i的入度等于A中第i列非零非无穷元素之和,出度即为A中第i行非零非无穷元素之和
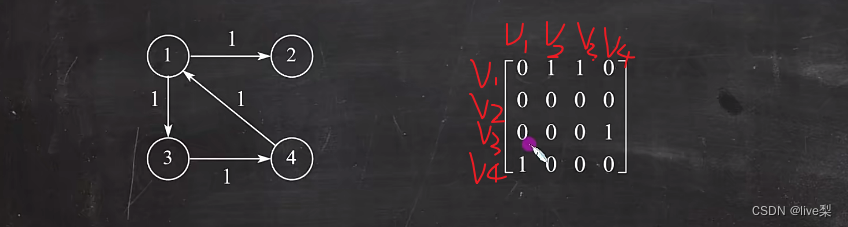
2.2邻接表法
①对于无向图

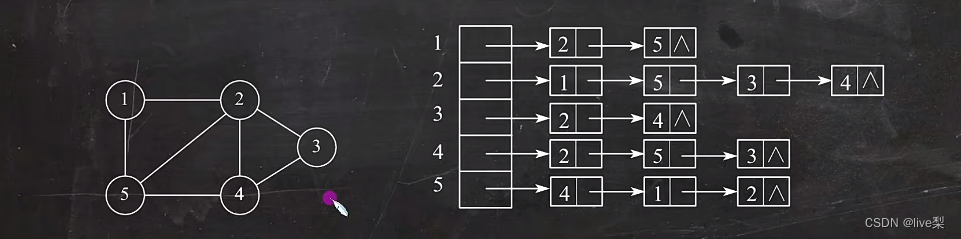
存储空间=O(|V|+2|E|) ,顶点存储1次,而边存储了2次。
②对于有向图


存储空间=O(|V|+|E|),边和顶点都只存储了1次。
特点:
①对于稀疏图,采用邻接表表示能够节省空间
②图的邻接表表示不唯一
③在有向图的邻接表表示中,求一个给定顶点的出度只需计算其邻接表中的结点个数。
④头结点指的是顶点,表结点指的是边。
2.3十字链表
针对无向图的邻接表法结点的入度难,采用十字链表法改进
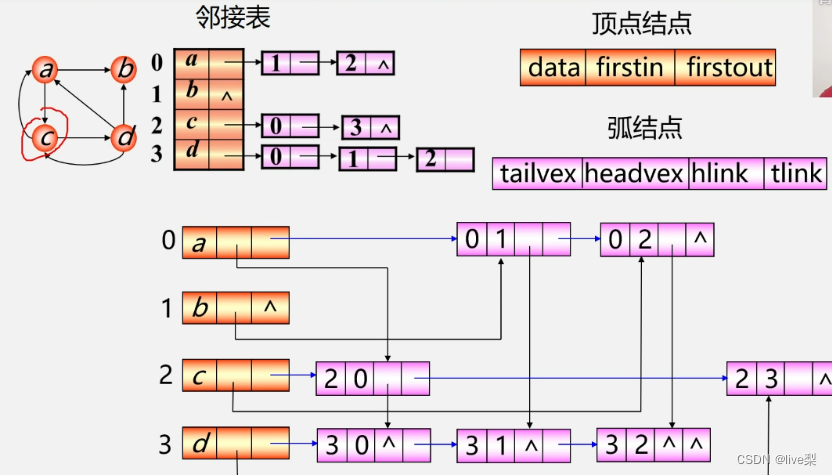
2.4邻接多重表
针对无向图中邻接表边存储2次的问题,采用邻接多重表法改进。
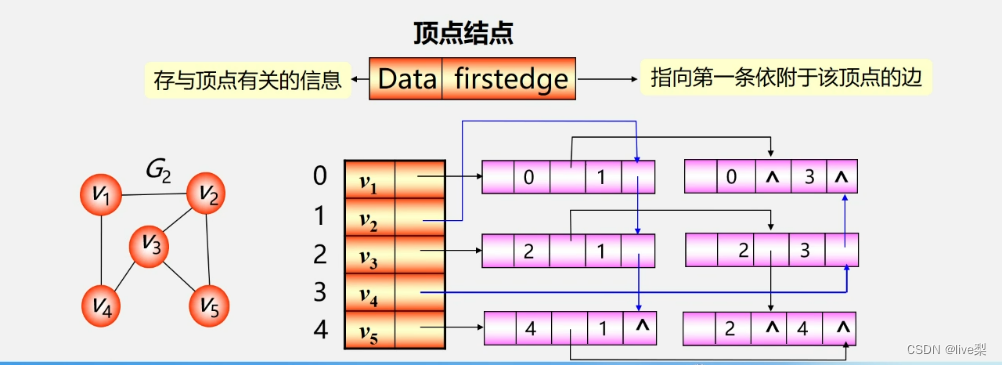
三、图的遍历
定义:从图中的某一点出发,按照某种搜索方法沿着图中所有顶点访问一次且仅访问一次
算法:广度优先搜索,深度优先搜索
3.1广度优先搜索
类似于二叉树的先序遍历,类似于树的层次遍历,例:
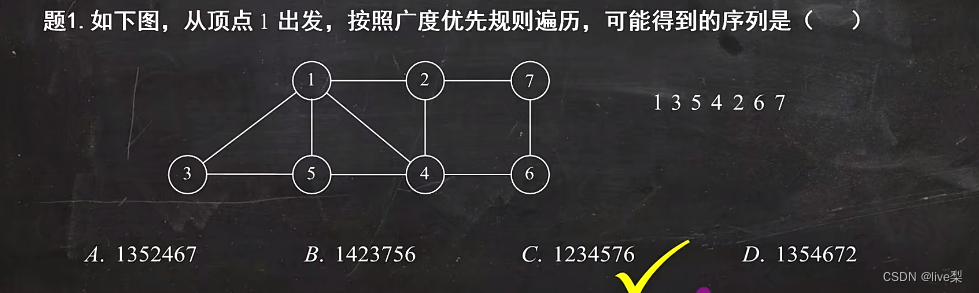
3.2深度优先搜索
类似于树的先序遍历,例:
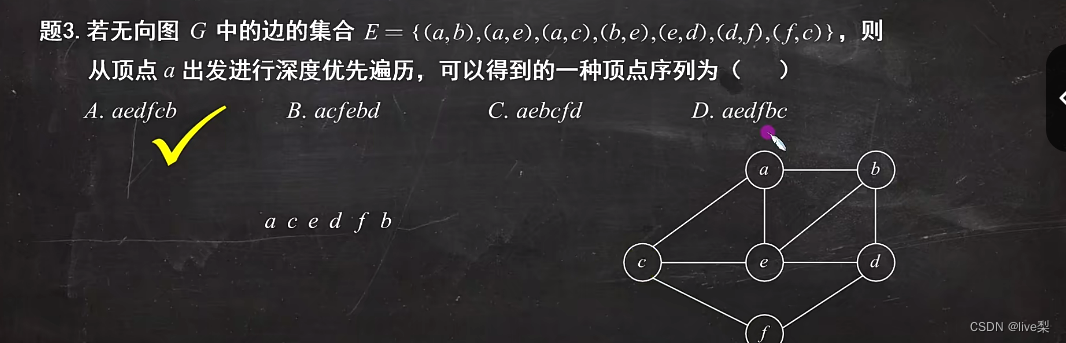
注:如果从一个无向图的任意顶点出发进行一次广度和深度优先搜索即可访问所有顶点,那么该图一定是连通图。
四、图的应用
4.1最小生成树
带权连通无向图中,所有生成树中权值之和最小的生成树。
4.1.1普里姆算法
①任取一顶点,去掉所有边
②选择一个与当前顶点集合距离最近的顶点,并将该顶点和相应的边加入进来,同时不能形成回路。
③重复②,直至图中所有顶点都并入。

4.1.2克鲁斯卡尔算法
①去掉所有边
②选边(权最小,且不构成回路)
③重复②,直至图中所有顶点都并入
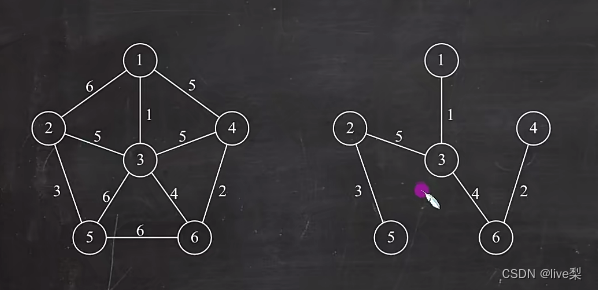
最小生成树边数=顶点数-1
4.2最短路径
4.2.1迪杰斯特拉算法

4.3拓扑排序
·AOV网:顶点表示活动,<Vi,Vj>
·每个顶点出现且只出现一次,若存在一条从顶点A到顶点B的路径,则在排序中顶点B出现在顶点A的后面。
算法实现:
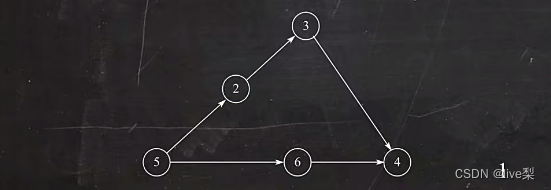
①从AOV网中选择一个没有前驱的顶点并输出
②从网中删除该顶点和所有以它为起点的有向边
③重复①②直到当前AOV网为空或当前网中不存在无前驱的顶点为止
 、
、
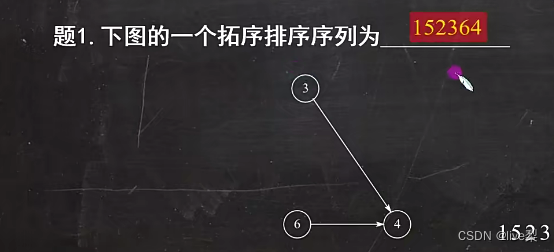
4.4关键路径
·AOE网:以顶点表示事件,以有向边表示活动,以边上的权值表示完成该活动的开销
·关键路径:从开始顶点到结束顶点的所有路径中,具有最大路径长度的路径
·关键活动:关键路径上的活动
算法实现:
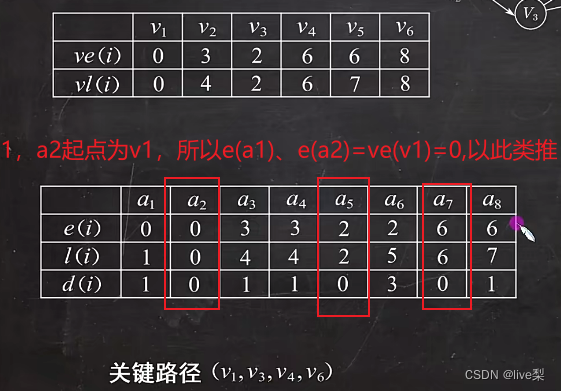
①令ve(源点)=0,求最早发生时间ve()
ve()=Max{ve(j)+weight(vj,vk)} (从前往后算)
②令vl(汇点)=ve(汇点),求最迟发生时间vl()
vl()=Min{vl(j)-weight(vk,vj)} (从后往前算)
③根据ve()值求所有弧的最早开始时间e()
e()=ve()
④根据vl()值求所有弧的最迟开始时间l()
l()=vl()-weight(vk,vj)
⑤求AOE网中所有活动的差额d(),找出所有d()=0的活动构成关键路径
d()=l()-e()
例:




![[SAP ABAP] 追加内表数据](https://img-blog.csdnimg.cn/direct/47730ae445c844d7b90b3ca829cb0874.png)