目录
编辑
绪论篇
有关知识表示和推理的零碎知识点
机器学习篇
K-近邻算法(KNN)
人工神经网络与深度学习篇
人工神经元模型
人工神经网络
BP神经网络
卷积神经网络
搜索策略
状态空间表示法
盲目搜索
启发式图搜索策略

绪论篇
3个学派:符号主义,连接主义,行为主义。
模型分类:决策式AI,生成式AI。
人类智能:很难给出确切的定义。
人类智能的特征/智能的能力:具有感知能力、具有记忆与思维能力、具有学习能力、具有行为能力。
认识智能的观点:思维理论,知识阈值理论,进化理论。
人工智能是用人工的方法在机器上实现的智能。
人工智能发展历史3个阶段:孕育、形成、发展。
人工智能领域研究的基本内容为知识表示、机器感知、机器思维、机器学习、机器行为等几个方面。
扩展:图灵测试——测试计算机是否具有智能

扩展:中文房间——证明机器不具有智能,不能理解人类语言的真正含义

有关知识表示和推理的零碎知识点
人工智能导论复习题和概念-CSDN博客
机器学习篇
机器学习分类(根据样本数据是否带有标签):监督的机器学习、无监督的机器学习、半监督学习。
监督学习又称为“有教师学习”。在监督学习中,模型采用有标签的数据集完成学习过程。
按任务的输出类型、监督学习可分为分类和回归两种。
无监督学习的特点是训练数据集中没有标签信息。
监督学习可完成分类和回归两种任务,非监督学习只能完成分类任务。
半监督学习介于二者之间,训练数据集只有一部分数据是有标签的,而其余的数据甚至大部分数据是没有标签的。将预测结果置信度比较高的“伪标签”加入训练集。
K-近邻算法(KNN)
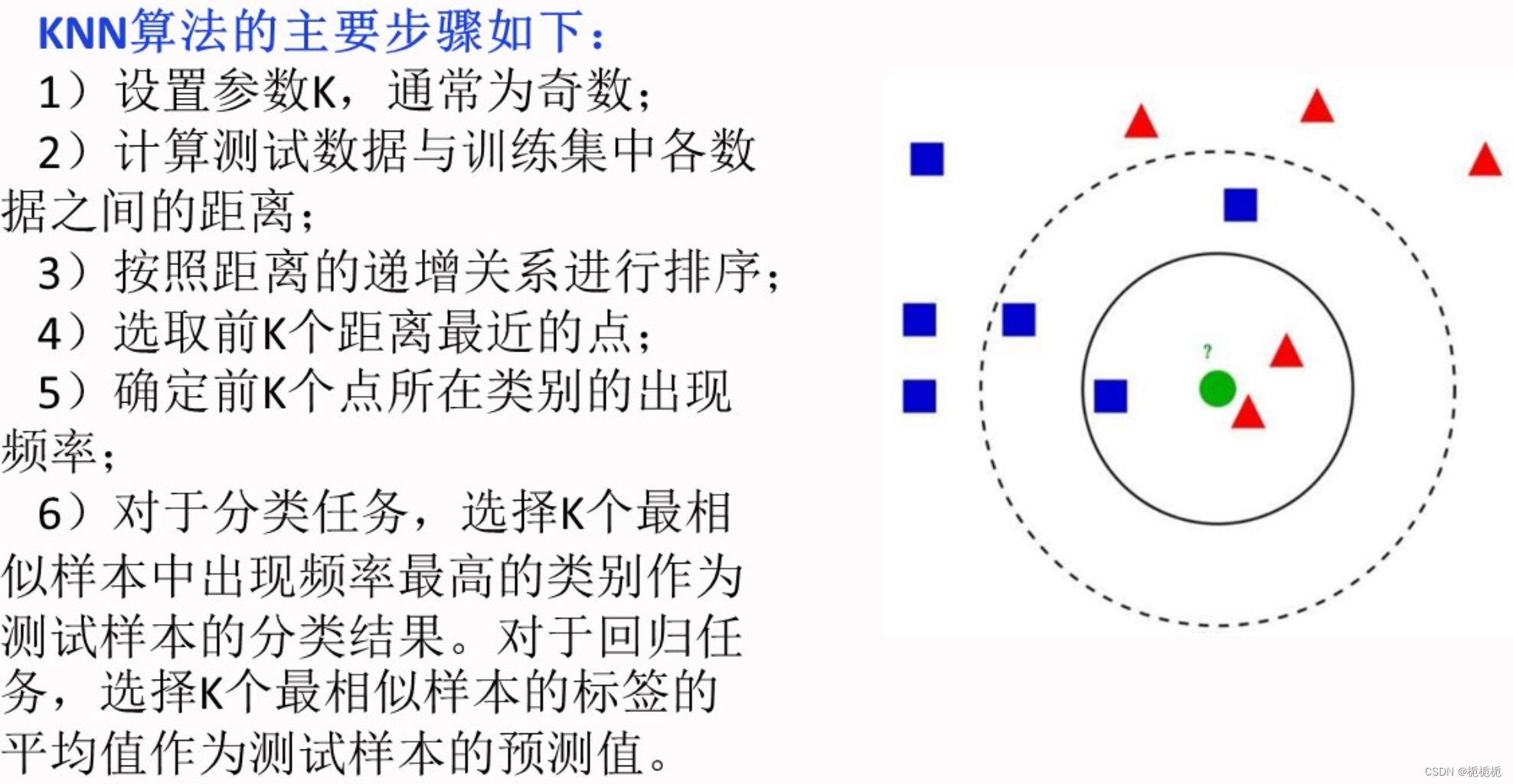
计算距离的方法有欧氏距离和曼哈顿距离

KNN算法优点:容易理解,理论成熟,既可以用来做分类,也可以用来做回归;可用于数值型数据和离散型数据;训练时间复杂度O(n);无数据输入假定;对异常值不敏感。
KNN算法缺点:算法复杂性高;空间复杂性高;当存在样本不均衡时,对稀有类别的预测准确率较低。
K-means 聚类算法
数学建模算法:K-means聚类算法 (qq.com)
支持向量机 SVM
机器学习之支持向量机(SVM)-CSDN博客
人工神经网络与深度学习篇
人工神经元模型

人工神经网络
按照拓扑结构建立神经元的连接。把许多单个神经元按照一定层次结构连接起来。人工神经网络是层级结构,每层神经元与下一层神经元全互连,神经元之间不存在同层连接,也不存在跨层连接。这样的神经网络结构通常称为“多层前馈神经网络”。
在多层前馈神经网络中,神经元可按层次分为三类:输入层神经元,输出层神经元和隐藏层神经元。

输入层不属于功能神经元。
参数计算:d个输入神经元,l个输出神经元,q个隐层神经元。
参数个数 = (d+l+1)*q+l
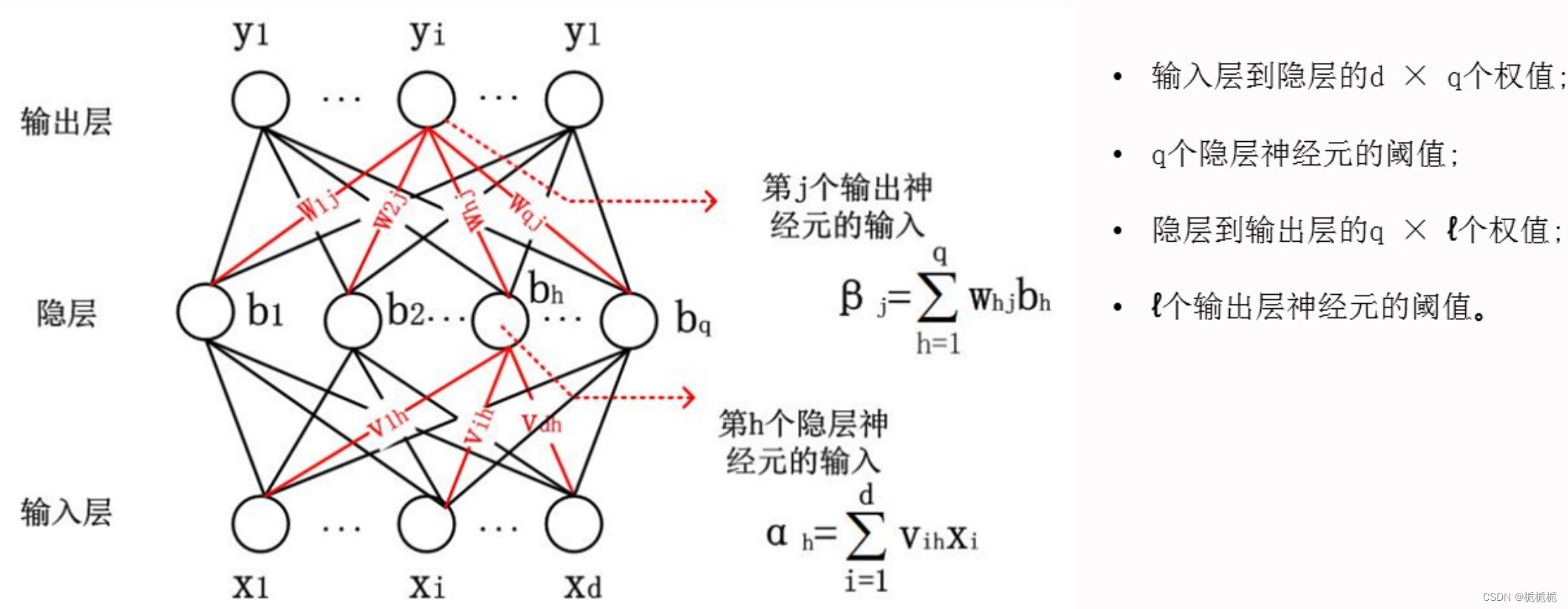
BP神经网络

卷积神经网络
与传统人工神经网络不同的是,卷积神经网络的基本单元不再是神经元,而是卷积核,多个卷积核构成了一个卷积层,多个卷积层顺次连接形成卷积层顺次连接形成卷积神经网络的层级结构。
!!!下面两篇大佬的高质量文(必看)!!!
卷积神经网络---详解卷积运算、池化操作(Pooling)_池化层操作流程-CSDN博客
深度学习CNN网络--卷积层、池化层、全连接层详解与其参数量计算_卷积层,池化层,全连接层-CSDN博客
卷积层
卷积层的参数量:由卷积核的大小、输入特征图的通道图以及输出特征图的通道数共同决定。对于每个卷积核,其参数量为卷积核宽度*卷积核高度*输入通道数。由于有多个卷积核,最终的参数量还需要乘以输出通道数的数量。如果考虑偏置项,则每个卷积核还会增加一个偏置参数。假设二维卷积层输入数据的通道数为N,卷积核的大小为K*K,当前卷积层卷积核的数量为M,则该卷积层的参数量为:(K*K*N+1)*M
卷积核的大小:较小的核有利于提供输入的细节特征,较大卷积核偏向于提取输入的宏观特征信息。
卷积层的深度:卷积层的深度指的是一个CNN中卷积层的层数。卷积层的深度决定了网络可以提取的特征的复杂性。更深的网络能学习更复杂的特征表示,但也增加了过拟合的风险和计算成本。
卷积步长:卷积层的卷积步长与填充方式直接决定了卷积操作后特征图的大小。假设原始图像大小为(其中n为像素值),卷积核大小为f,步长大小为s,则卷积操作后特征图大小m*m,其关系式为:
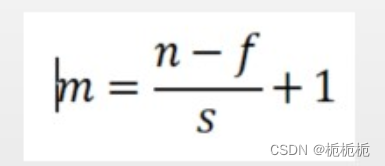
若输入图像6*6,卷积核3*3,步长1,则特征图大小为6-3+1=4
填充方式:控制特征图大小。设p为填充大小,填充后特征图大小m=(n-f+2p)/s+1

池化层:平均池化和最大池化。通过降低特征图的维度来减少网络中的参数数量和计算复杂度,有助于防止过拟合,提高模型的泛化能力;增强网络对小的平移和形变的鲁棒性,因为他丢弃了位置信息,只保留最重要的特征信息。
全连接层:扮演着“分类器”的角色。负责将由卷积层和池化层提取的特征映射到样本的标记空间,从而实现分类和回归分析。
LeNet-5模型:C1(卷积)->S2(池化)->C3(卷积)->S4(池化)->C5(卷积)->F6(全连接)
搜索策略
状态空间表示法
八数码问题
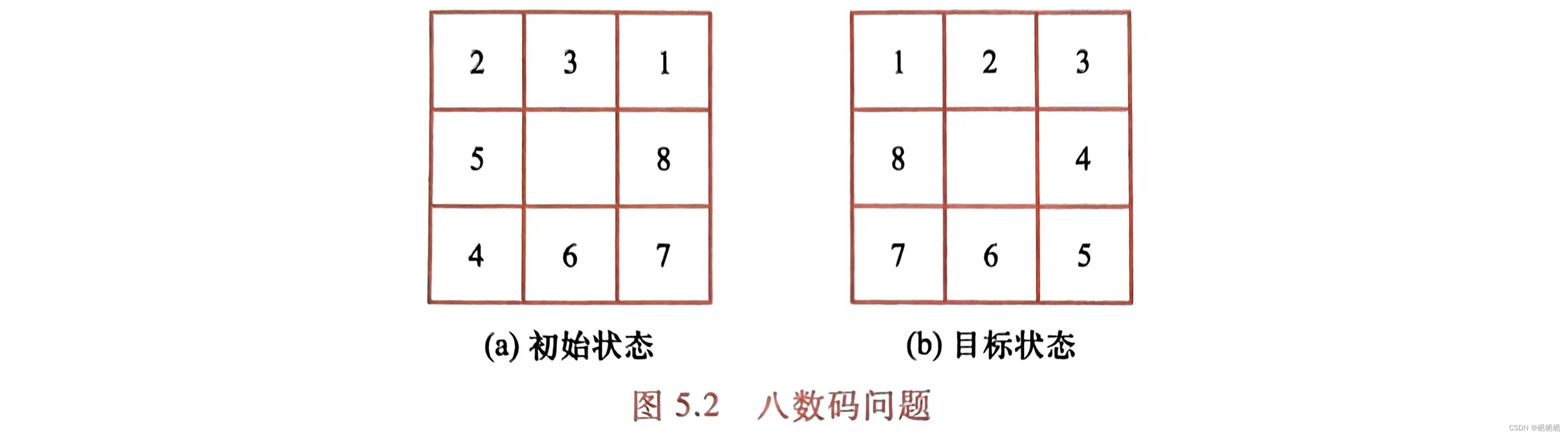

盲目搜索
宽度优先搜索
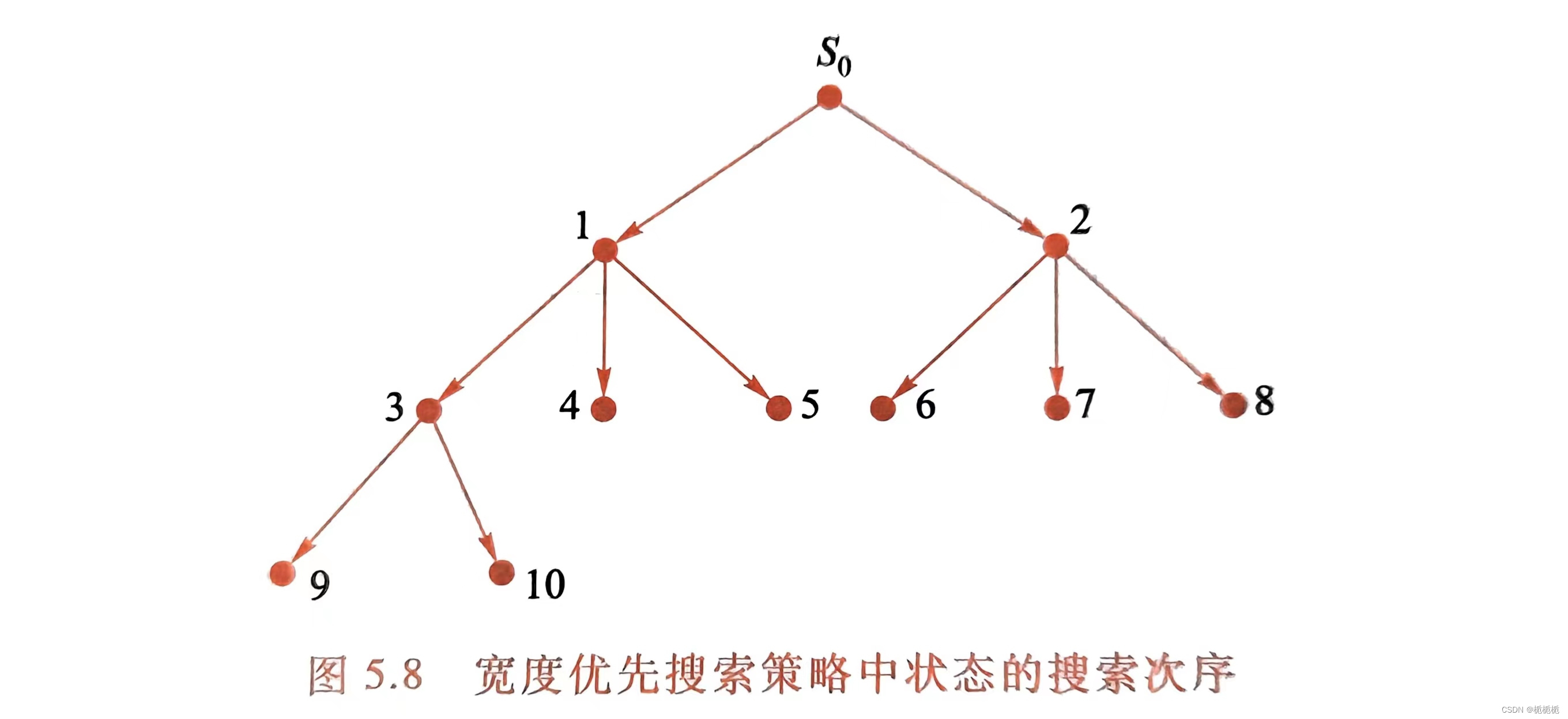
积木问题的优先搜索树:通过搬动积木块,从初始状态达到目标状态,积木A在顶部,积木B在中间,积木C在底部。

深度优先搜索

启发式图搜索策略
在具体求解中,能够利用与该问题有关的信息来简化搜索过程,成此类信息为启发信息,而这种利用启发信息的搜索过程为启发式搜索。
A搜索算法是寻找并设计一个与问题有关的h(n)及构造出f(n)=g(n)+h(n),然后以f(n)的大小来排序待扩展状态的次序,每次选择f(n)值最小者进行扩展。
f(n)评价函数,g(n)从初始结点到n结点的实际代价,h(n)从n结点到目的结点的最佳路径的估计代价。
定义h*(n)为状态n到目的状态的最优路径的代价。对一具体问题,只要有解,则一定存在h*(n)。当要求估价函数中的h(n)都小于等于h*(n)时,A搜索算法就成为A*搜索算法。
A*,h(n)<=h*(n)