二叉树DFS、BFS

news2024/10/6 16:17:31

目录

1，DFS遍历

2，DFS遍历OJ实战

力扣 144. 二叉树的前序遍历

力扣 94. 二叉树的中序遍历

力扣 145. 二叉树的后序遍历

力扣 105. 从前序与中序遍历序列构造二叉树

力扣 106. 从中序与后序遍历序列构造二叉树

力扣 889. 根据前序和后序遍历构造二叉树

CSU 1283 Binary Tree Traversals

力扣 404. 左叶子之和

力扣 1430. 判断给定的序列是否是二叉树从根到叶的路径

力扣 1973. 值等于子节点值之和的节点数量

力扣 1120. 子树的最大平均值

力扣 1612. 检查两棵二叉表达式树是否等价

3，BFS遍历

力扣 102. 二叉树的层序遍历

力扣 107. 二叉树的层序遍历 II

力扣 1161. 最大层内元素和

剑指 Offer 32 - I. 从上到下打印二叉树

剑指 Offer 32 - III. 从上到下打印二叉树 III

力扣 1602. 找到二叉树中最近的右侧节点

1，DFS遍历

ACM模板——二叉树

仅由1种遍历无法确定二叉树，中序 + 先序或后序 可以确定二叉树，
先序 + 后序 可能可以确定二叉树,也可能不可以。

大学数据结构实验：

根据输入的数据建立一个二叉树；
分别采用前序、中序、后序的遍历方式显示输出二叉树的遍历结果

代码：

#include<iostream>
using namespace std;
 
struct node			//定义结点
{
	char ch;
	struct node *lchild;
	struct node *rchild;
};
 
node * create(struct node *p)				//利用递归函数，按照先序创建二叉树，以0代表空
{
	char c;
	cin >> c;
	if (c == '0')p = NULL;
	else
	{
		p = new  node;
		p->ch = c;
		p->lchild = create(p->lchild);
		p->rchild = create(p->rchild);
	}
	return p;
}
 
void preOrder(node *p)			//利用递归函数，先序遍历
{
	if (p)
	{
		cout << p->ch << " ";
		preOrder(p->lchild);
		preOrder(p->rchild);
	}
}
 
void inOrder(node *p)			//利用递归函数，中序遍历
{
	if (p)
	{
		inOrder(p->lchild);
		cout << p->ch << " ";
		inOrder(p->rchild);
	}
}
 
void postOrder(node *p)			//利用递归函数，后序遍历
{
	if (p)
	{
		postOrder(p->lchild);
		postOrder(p->rchild);
		cout << p->ch << " ";
	}
}
 
int main()
{
	node *root = new  node;
	cout << "输入二叉树存储的字符，以0表示不存在" << endl;
	root = create(root);			//易错点1
	cout << "先序遍历是    ";
	preOrder(root);
	cout << endl << "中序遍历是    ";
	inOrder(root);
	cout << endl << "后序遍历是    ";
	postOrder(root);
	system("pause>nul");
	return 0;
}

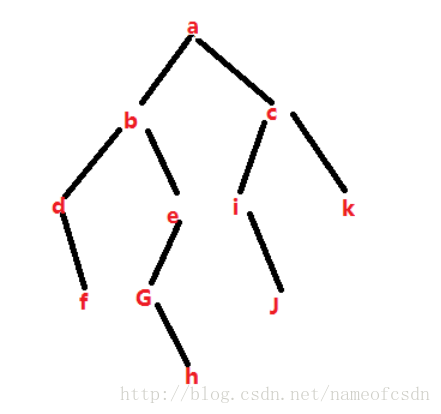
用来测试的二叉树：

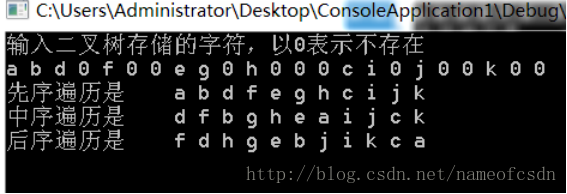
运行结果：

2，DFS遍历OJ实战

力扣 144. 二叉树的前序遍历

题目：

给定一个二叉树，返回它的 前序 遍历。

 示例:

输入: [1,null,2,3]  
   1
    \
     2
    /
   3 

输出: [1,2,3]
进阶: 递归算法很简单，你可以通过迭代算法完成吗？

代码：

class Solution {
public:
	vector<int> preorderTraversal(TreeNode* root) {
		vector<int>v1;
		if (root == NULL)return v1;
		v1.insert(v1.end(), root->val);
		vector<int>v2 = preorderTraversal(root->left);
		v1.insert(v1.end(), v2.begin(), v2.end());
		v2 = preorderTraversal(root->right);
		v1.insert(v1.end(), v2.begin(), v2.end());
		return v1;
	}
};

力扣 94. 二叉树的中序遍历

题目：

给定一个二叉树，返回它的中序 遍历。

示例:

输入: [1,null,2,3]
   1
    \
     2
    /
   3

输出: [1,3,2]
进阶: 递归算法很简单，你可以通过迭代算法完成吗？

代码：

class Solution {
public:
	vector<int> inorderTraversal(TreeNode* root) {
		vector<int>v1;
		if (root == NULL)return v1;
		v1 = inorderTraversal(root->left);
		v1.insert(v1.end(), root->val);
		vector<int>v2 = inorderTraversal(root->right);
		v1.insert(v1.end(), v2.begin(), v2.end());
		return v1;
	}
};

力扣 145. 二叉树的后序遍历

题目：

给定一个二叉树，返回它的 后序 遍历。

示例:

输入: [1,null,2,3]  
   1
    \
     2
    /
   3 

输出: [3,2,1]
进阶: 递归算法很简单，你可以通过迭代算法完成吗？

代码：

class Solution {
public:
	vector<int> postorderTraversal(TreeNode* root) {
		vector<int>v1;
		if (root == NULL)return v1;		
		vector<int>v2 = postorderTraversal(root->left);
		v1.insert(v1.end(), v2.begin(), v2.end());
		v2 = postorderTraversal(root->right);
		v1.insert(v1.end(), v2.begin(), v2.end());
		v1.insert(v1.end(), root->val);
		return v1;
	}
};

力扣 105. 从前序与中序遍历序列构造二叉树

根据一棵树的前序遍历与中序遍历构造二叉树。

注意:
你可以假设树中没有重复的元素。

例如，给出

前序遍历 preorder = [3,9,20,15,7]
中序遍历 inorder = [9,3,15,20,7]
返回如下的二叉树：

    3
   / \
  9  20
    /  \
   15   7

class Solution {
public:
    TreeNode* buildTree(vector<int>& preorder,int s1, vector<int>& inorder, int s2, int len) {
        if(len<=0)return NULL;
        TreeNode *ans=new TreeNode;
        ans->val=preorder[s1];
        auto loc=find(inorder.begin()+s2,inorder.begin()+s2+len,preorder[s1]);
        ans->left=buildTree(preorder,s1+1,inorder,s2,loc-inorder.begin()-s2);
        ans->right=buildTree(preorder,loc-inorder.begin()-s2+s1+1,inorder,loc-inorder.begin()+1,len-(loc-inorder.begin()-s2)-1);
        return ans;
    }
    TreeNode* buildTree(vector<int>& preorder, vector<int>& inorder) {
        return buildTree(preorder,0,inorder,0,inorder.size());
    }
};

力扣 106. 从中序与后序遍历序列构造二叉树

根据一棵树的中序遍历与后序遍历构造二叉树。

注意:
你可以假设树中没有重复的元素。

例如，给出

中序遍历 inorder = [9,3,15,20,7]
后序遍历 postorder = [9,15,7,20,3]
返回如下的二叉树：

    3
   / \
  9  20
    /  \
   15   7

class Solution {
public:
    TreeNode* buildTree(vector<int>& postorder,int s1, vector<int>& inorder,int s2, int len) {
        if(len<=0)return NULL;
        TreeNode *ans=new TreeNode;
        ans->val=postorder[s1+len-1];
        auto loc=find(inorder.begin()+s2,inorder.begin()+s2+len,postorder[s1+len-1]);
        ans->left=buildTree(postorder,s1,inorder,s2,loc-inorder.begin()-s2);
        ans->right=buildTree(postorder,loc-inorder.begin()-s2+s1,inorder,loc-inorder.begin()+1,len-(loc-inorder.begin()-s2)-1);
        return ans;
    }
    TreeNode* buildTree(vector<int>& inorder, vector<int>& postorder) {
        return buildTree(postorder,0,inorder,0,inorder.size());
    }
};

力扣 889. 根据前序和后序遍历构造二叉树

返回与给定的前序和后序遍历匹配的任何二叉树。

 pre 和 post 遍历中的值是不同的正整数。

示例：

输入：pre = [1,2,4,5,3,6,7], post = [4,5,2,6,7,3,1]
输出：[1,2,3,4,5,6,7]
 

提示：

1 <= pre.length == post.length <= 30
pre[] 和 post[] 都是 1, 2, ..., pre.length 的排列
每个输入保证至少有一个答案。如果有多个答案，可以返回其中一个。

class Solution {
public:
    TreeNode* buildTree(vector<int>& preorder,int s1, vector<int>& inorder, int s2, int len) {
        if(len<=0)return NULL;
        TreeNode *ans=new TreeNode;
        ans->val=preorder[s1];
        if(len==1)return ans;
        auto loc=find(inorder.begin()+s2,inorder.begin()+s2+len,preorder[s1+1]);
        ans->left=buildTree(preorder,s1+1,inorder,s2,loc-inorder.begin()-s2+1);
        ans->right=buildTree(preorder,loc-inorder.begin()-s2+s1+2,inorder,loc-inorder.begin()+1,len-(loc-inorder.begin()-s2)-2);
        return ans;
    }
    TreeNode* constructFromPrePost(vector<int>& preorder, vector<int>& inorder) {
        return buildTree(preorder,0,inorder,0,inorder.size());
    }
};

CSU 1283 Binary Tree Traversals

题目：

Description

给定一棵二叉树先序遍历得到的先序序列和后续遍历得到的后序序列，能够唯一确定这棵二叉树吗？

Input

输入数据的第一行包含一个整数T (1 <= T <= 100)，表示接下来一共有T组测试数据。

对于每组测试数据，第一行包含一个正整数N (1 <= N <= 26)，表示这棵二叉树一共有N个节点。接下来两行每行均包含N个互不相同的大写字母，字符之间没有空格，分别表示对这棵二叉树进行先序遍历和后序遍历后得到的先序序列和后序序列。数据保证根据先序序列和后续序列至少能够构造出一棵二叉树。

Output

对于每组测试数据，如果根据先序序列和后续序列能够唯一确定一棵二叉树，用一行输出N个大写字母，字符之间不应有空格，表示这棵二叉树的中序序列。如果不能唯一确定一棵二叉树，则用一行输出“-1”（不包括引号）。

Sample Input

2
2
AB
BA
3
ABC
BCA

Sample Output

-1
BAC

代码：

#include<iostream>
using namespace std;
 
char s1[27], s2[27], s3[27];
 
bool f(int k1, int k2, int k3, int len)
{
	if (len == 1)
	{
		s3[k3] = s1[k1];
		return true;
	}
	char c = s1[k1 + 1];
	for (int i = k2; i < k2 + len; i++)
	{
		if (s2[i] != c)continue;
		if (i == k2 + len - 2)return false;
		if (!f(k1 + 1, k2, k3, i - k2 + 1))return false;
		if (!f(k1 - k2 + i + 2, i + 1, k3 - k2 + i + 2, k2 + len - 2 - i))return false;
		s3[k3 - k2 + i + 1] = s1[k1];
	}
	return true;
}
 
int main()
{
	int t, n;
	cin >> t;	
	while (t--)
	{
		cin >> n >> s1 >> s2;
		s3[n] = '\0';
		if (f(0, 0, 0, n))cout << s3 << endl;
		else cout << "-1\n";
	}
	return 0;
}

力扣 404. 左叶子之和

给定二叉树的根节点 root ，返回所有左叶子之和。

示例 1：

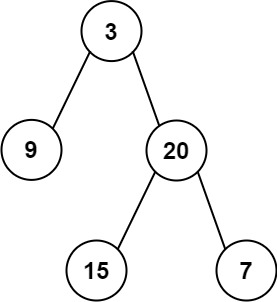
输入: root = [3,9,20,null,null,15,7] 
输出: 24 
解释: 在这个二叉树中，有两个左叶子，分别是 9 和 15，所以返回 24
示例 2:

输入: root = [1]
输出: 0
 

提示:

节点数在 [1, 1000] 范围内
-1000 <= Node.val <= 1000

class Solution {
public:
	void sumOfLeftLeaves(TreeNode* root, bool isLeft) {
		if (!root->left && !root->right) {
			if(isLeft)s += root->val;
			return;
		}
		if (root->left)sumOfLeftLeaves(root->left, true);
		if (root->right)sumOfLeftLeaves(root->right, false);
	}
	int sumOfLeftLeaves(TreeNode* root) {
		if (!root)return 0;
		s = 0;
		sumOfLeftLeaves(root, false);
		return s;
	}
private:
	int s;
};

力扣 1430. 判断给定的序列是否是二叉树从根到叶的路径

给定一个二叉树，我们称从根节点到任意叶节点的任意路径中的节点值所构成的序列为该二叉树的一个 “有效序列” 。检查一个给定的序列是否是给定二叉树的一个 “有效序列” 。

我们以整数数组 arr 的形式给出这个序列。从根节点到任意叶节点的任意路径中的节点值所构成的序列都是这个二叉树的 “有效序列” 。

示例 1：

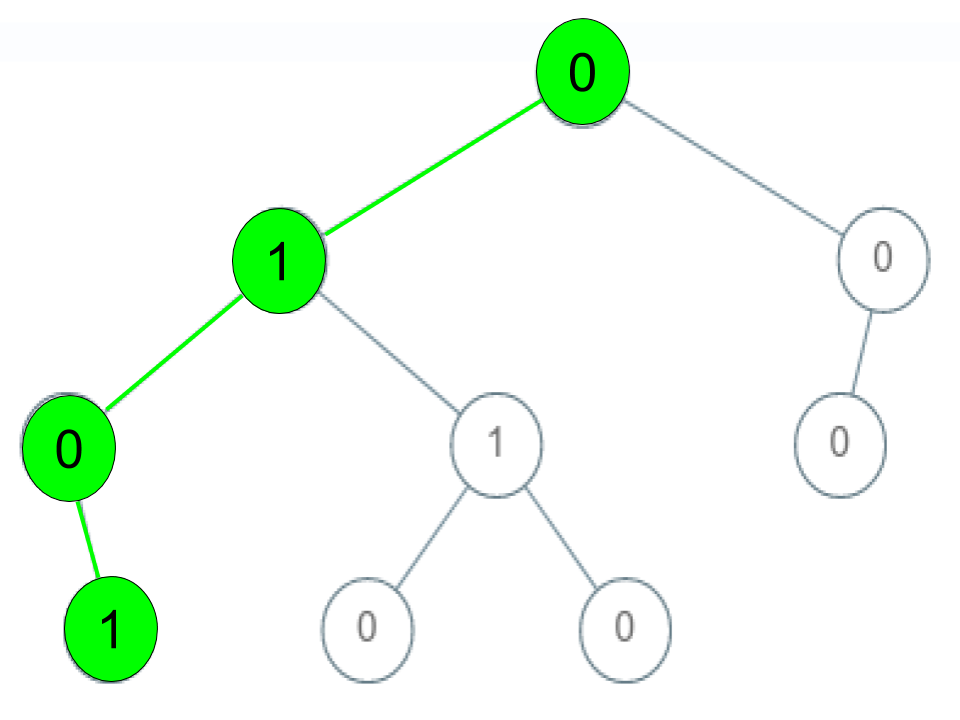
输入：root = [0,1,0,0,1,0,null,null,1,0,0], arr = [0,1,0,1]
输出：true
解释：
路径 0 -> 1 -> 0 -> 1 是一个“有效序列”（图中的绿色节点）。
其他的“有效序列”是：
0 -> 1 -> 1 -> 0 
0 -> 0 -> 0
示例 2：

输入：root = [0,1,0,0,1,0,null,null,1,0,0], arr = [0,0,1]
输出：false 
解释：路径 0 -> 0 -> 1 不存在，所以这不是一个“序列”。
示例 3：

输入：root = [0,1,0,0,1,0,null,null,1,0,0], arr = [0,1,1]
输出：false
解释：路径 0 -> 1 -> 1 是一个序列，但不是一个“有效序列”（译者注：因为序列的终点不是叶节点）。
 

提示：

1 <= arr.length <= 5000
0 <= arr[i] <= 9
每个节点的值的取值范围是 [0 - 9]

class Solution {
public:
	bool dfs(TreeNode* root, vector<int>& arr, int loc)
	{
		if (root->val != arr[loc])return false;
		if (!root->left && !root->right && loc == arr.size() - 1)return true;
		if ((!root->left && !root->right) || loc == arr.size() - 1)return false;
		if(root->left && dfs(root->left, arr, loc + 1))return true;
		if(root->right && dfs(root->right, arr, loc + 1))return true;
		return false;
	}
	bool isValidSequence(TreeNode* root, vector<int>& arr) {
		if (!root)return false;
		return dfs(root, arr, 0);
	}
};

力扣 1973. 值等于子节点值之和的节点数量

给定一颗二叉树的根节点 root ，返回满足条件：节点的值等于该节点所有子节点的值之和 的节点的数量。

一个节点 x 的 子节点 是指从节点 x 出发，到所有叶子节点路径上的节点。没有子节点的节点的子节点和视为 0 。

示例 1:

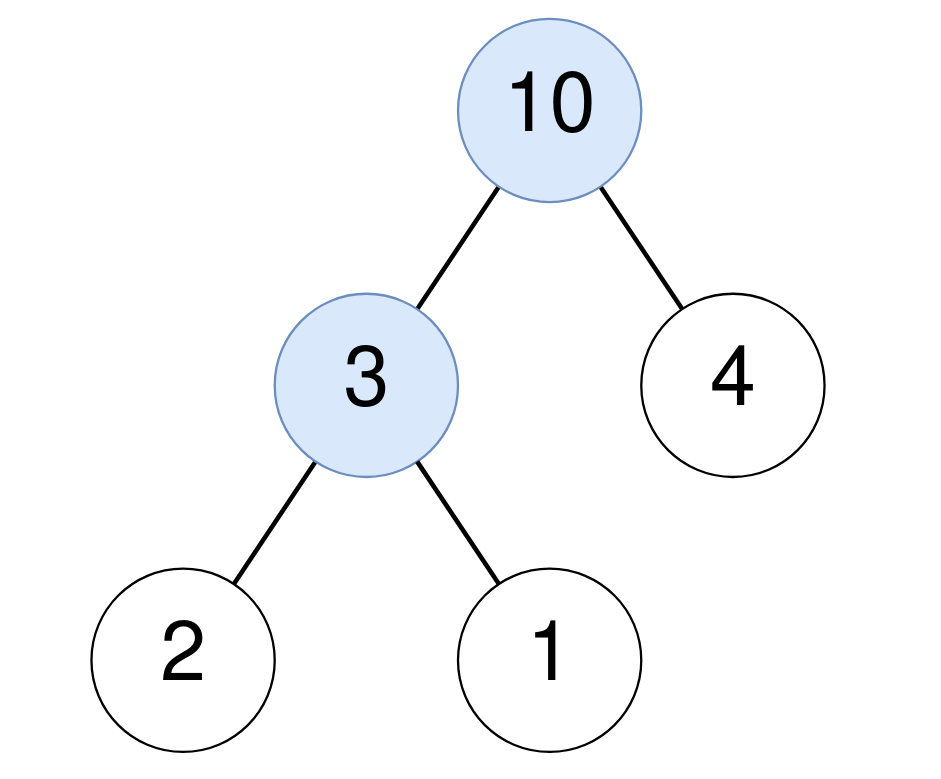
输入: root = [10,3,4,2,1]
输出: 2
解释:
对于值为10的节点: 其子节点之和为： 3+4+2+1 = 10。
对于值为3的节点：其子节点之和为： 2+1 = 3。

示例 2:

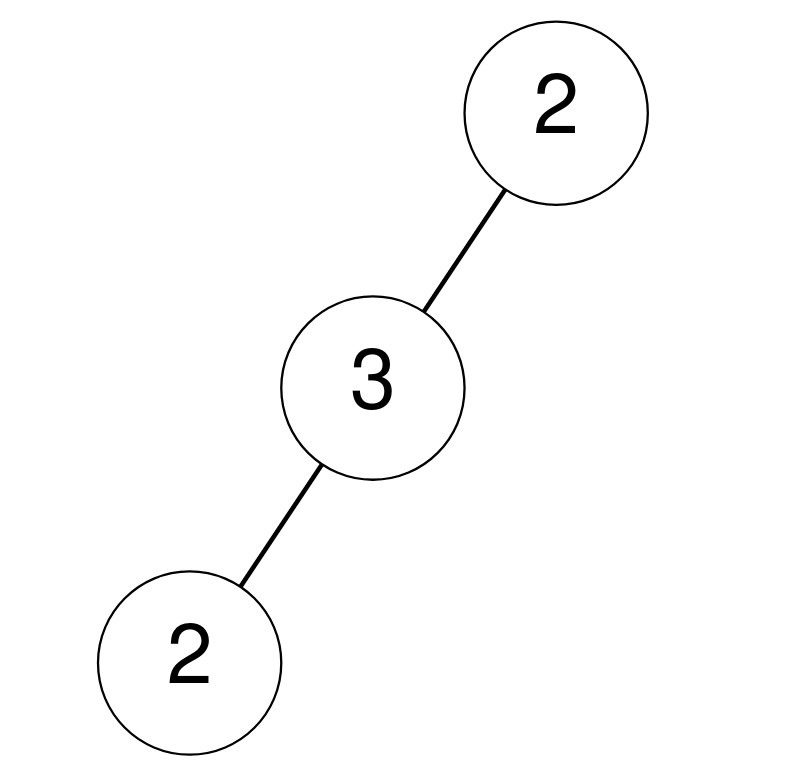
输入: root = [2,3,null,2,null]
输出: 0
解释:
没有节点满足其值等于子节点之和。

示例 3:

输入: root = [0]
输出: 1
解释:
对于值为0的节点：因为它没有子节点，所以自己点之和为0。

提示：

  • 树中节点的数量范围： [1, 105]
  • 0 <= Node.val <= 105
class Solution {
public:
	int ans = 0;
	long long dfs(TreeNode* root)
	{
		if (!root)return 0;
		long long n = dfs(root->left) + dfs(root->right);
		if (root->val == n)ans++;
		return root->val + n;
	}
	int equalToDescendants(TreeNode* root) {
		dfs(root);
		return ans;
	}
};

力扣 1120. 子树的最大平均值

 给你一棵二叉树的根节点 root，找出这棵树的 每一棵 子树的 平均值 中的 最大 值。

子树是树中的任意节点和它的所有后代构成的集合。

树的平均值是树中节点值的总和除以节点数。

示例：

输入：[5,6,1]
输出：6.00000
解释： 
以 value = 5 的节点作为子树的根节点，得到的平均值为 (5 + 6 + 1) / 3 = 4。
以 value = 6 的节点作为子树的根节点，得到的平均值为 6 / 1 = 6。
以 value = 1 的节点作为子树的根节点，得到的平均值为 1 / 1 = 1。
所以答案取最大值 6。
 

提示：

树中的节点数介于 1 到 5000之间。
每个节点的值介于 0 到 100000 之间。
如果结果与标准答案的误差不超过 10^-5，那么该结果将被视为正确答案。

class Solution {
public:
	double ans = -1234567;
	void dfs(TreeNode* root, int& s, int& num)
	{
		if (!root) {
			s = 0, num = 0;
			return;
		}
		int s1, num1, s2, num2;
		dfs(root->left, s1, num1);
		dfs(root->right, s2, num2);
		s = s1 + s2 + root->val, num = num1 + num2 + 1;
		ans = max(ans, s * 1.0 / num);
	}
	double maximumAverageSubtree(TreeNode* root) {
		int s, num;
		dfs(root, s, num);
		return ans;
	}
};

力扣 1612. 检查两棵二叉表达式树是否等价

二叉表达式树是一种表达算术表达式的二叉树。二叉表达式树中的每一个节点都有零个或两个子节点。 叶节点（有 0 个子节点的节点）表示操作数，非叶节点（有 2 个子节点的节点）表示运算符。在本题中，我们只考虑 '+' 运算符（即加法）。

给定两棵二叉表达式树的根节点 root1 和 root2 。如果两棵二叉表达式树等价，返回 true ，否则返回 false 。

当两棵二叉搜索树中的变量取任意值，分别求得的值都相等时，我们称这两棵二叉表达式树是等价的。

示例 1:

输入： root1 = [x], root2 = [x]
输出： true
示例 2:

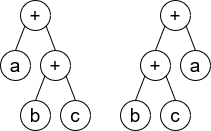
输入：root1 = [+,a,+,null,null,b,c], root2 = [+,+,a,b,c]
输出：true
解释：a + (b + c) == (b + c) + a
示例 3:

输入： root1 = [+,a,+,null,null,b,c], root2 = [+,+,a,b,d]
输出： false
解释： a + (b + c) != (b + d) + a
 

提示：

两棵树中的节点个数相等，且节点个数为范围 [1, 4999] 内的奇数。
Node.val 是 '+' 或小写英文字母。
给定的树保证是有效的二叉表达式树。
 

进阶：当你的答案需同时支持 '-' 运算符（减法）时，你该如何修改你的答案

template<typename T>
vector<T> vecAdd(const vector<T>& v1, const vector<T>& v2)
{
	vector<T>v(max(v1.size(), v2.size()));
	for (int i = 0; i < v.size(); i++)v[i] = 0;
	for (int i = 0; i < v1.size(); i++)v[i] += v1[i];
	for (int i = 0; i < v2.size(); i++)v[i] += v2[i];
	return v;
}

class Solution {
public:
	vector<int> dfs(Node* r)
	{
		vector<int> v(26);
		if (!r)return v;
		if (r->val >= 'a' && r->val <= 'z')v[r->val - 'a'] = 1;
		vector<int>v1 = dfs(r->left);
		vector<int>v2 = dfs(r->right);
		v = vecAdd(v, v1);
		v = vecAdd(v, v2);
		return v;
	}
	bool checkEquivalence(Node* r1, Node* r2) {
		vector<int> v1 = dfs(r1);
		vector<int> v2 = dfs(r2);
		for (int i = 0; i < 26; i++)if (v1[i] != v2[i])return false;
		return true;
	}
};

3，BFS遍历

力扣 102. 二叉树的层序遍历

给你一个二叉树，请你返回其按 层序遍历 得到的节点值。 （即逐层地，从左到右访问所有节点）。

示例：
二叉树：[3,9,20,null,null,15,7],

    3
   / \
  9  20
    /  \
   15   7
返回其层序遍历结果：

[
  [3],
  [9,20],
  [15,7]
]

class Solution {
public:
    void levelOrder(vector<vector<TreeNode*>>&v){
        vector<TreeNode*>v1=*(v.end()-1);
        vector<TreeNode*>v2;
        for(int i=0;i<v1.size();i++){
            if(v1[i]->left)v2.push_back(v1[i]->left);
            if(v1[i]->right)v2.push_back(v1[i]->right);
        }
        if(v2.empty())return;
        v.push_back(v2);
        levelOrder(v);
    }
    vector<vector<int>> levelOrder(TreeNode* root) {
        vector<vector<TreeNode*>>v;
        vector<TreeNode*>tmp;
        vector<vector<int>>ans;
        vector<int>tmpans;
        if(!root)return ans;
        tmp.push_back(root);
        v.push_back(tmp);
        levelOrder(v);
        for(int i=0;i<v.size();i++){
            tmpans.resize(v[i].size());
            for(int j=0;j<v[i].size();j++)tmpans[j]=v[i][j]->val;
            ans.push_back(tmpans);
        }
        return ans;
    }
};

力扣 107. 二叉树的层序遍历 II

给定一个二叉树，返回其节点值自底向上的层序遍历。 （即按从叶子节点所在层到根节点所在的层，逐层从左向右遍历）

例如：
给定二叉树 [3,9,20,null,null,15,7],

    3
   / \
  9  20
    /  \
   15   7
返回其自底向上的层序遍历为：

[
  [15,7],
  [9,20],
  [3]
]

和力扣 102. 二叉树的层序遍历是一样的，只需要翻转一下即可。

class Solution {
public:
    void levelOrder(vector<vector<TreeNode*>>&v){
        vector<TreeNode*>v1=*(v.end()-1);
        vector<TreeNode*>v2;
        for(int i=0;i<v1.size();i++){
            if(v1[i]->left)v2.push_back(v1[i]->left);
            if(v1[i]->right)v2.push_back(v1[i]->right);
        }
        if(v2.empty())return;
        v.push_back(v2);
        levelOrder(v);
    }
    vector<vector<int>> levelOrderBottom(TreeNode* root) {
        vector<vector<TreeNode*>>v;
        vector<TreeNode*>tmp;
        vector<vector<int>>ans;
        vector<int>tmpans;
        if(!root)return ans;
        tmp.push_back(root);
        v.push_back(tmp);
        levelOrder(v);
        for(int i=v.size()-1;i>=0;i--){
            tmpans.resize(v[i].size());
            for(int j=0;j<v[i].size();j++)tmpans[j]=v[i][j]->val;
            ans.push_back(tmpans);
        }
        return ans;
    }
};

力扣 1161. 最大层内元素和

给你一个二叉树的根节点 root。设根节点位于二叉树的第 1 层，而根节点的子节点位于第 2 层，依此类推。

请返回层内元素之和 最大 的那几层（可能只有一层）的层号，并返回其中 最小 的那个。

示例 1：

输入：root = [1,7,0,7,-8,null,null]
输出：2
解释：
第 1 层各元素之和为 1，
第 2 层各元素之和为 7 + 0 = 7，
第 3 层各元素之和为 7 + -8 = -1，
所以我们返回第 2 层的层号，它的层内元素之和最大。
示例 2：

输入：root = [989,null,10250,98693,-89388,null,null,null,-32127]
输出：2
 

提示：

树中的节点数在 [1, 104]范围内
-105 <= Node.val <= 105

class Solution {
public:
	void levelOrder(vector<vector<TreeNode*>>&v) {
		vector<TreeNode*>v1 = *(v.end() - 1);
		vector<TreeNode*>v2;
		for (int i = 0; i < v1.size(); i++) {
			if (v1[i]->left)v2.push_back(v1[i]->left);
			if (v1[i]->right)v2.push_back(v1[i]->right);
		}
		if (v2.empty())return;
		v.push_back(v2);
		levelOrder(v);
	}
	vector<vector<int>> levelOrder(TreeNode* root) {
		vector<vector<TreeNode*>>v;
		vector<TreeNode*>tmp;
		vector<vector<int>>ans;
		vector<int>tmpans;
		if (!root)return ans;
		tmp.push_back(root);
		v.push_back(tmp);
		levelOrder(v);
		for (int i = 0; i < v.size(); i++) {
			tmpans.resize(v[i].size());
			for (int j = 0; j < v[i].size(); j++)tmpans[j] = v[i][j]->val;
			ans.push_back(tmpans);
		}
		return ans;
	}
	int maxLevelSum(TreeNode* root) {
		vector<vector<int>>v = levelOrder(root);
		int m = INT_MIN;
		int ans = 0;
		for (int i = 0; i < v.size(); i++) {
			int s = 0;
			for (auto vi : v[i])s += vi;
			if (m < s)m = s, ans = i + 1;
		}
		return ans;
	}
};

剑指 Offer 32 - I. 从上到下打印二叉树

从上到下打印出二叉树的每个节点，同一层的节点按照从左到右的顺序打印。

例如:
给定二叉树: [3,9,20,null,null,15,7],

    3
   / \
  9  20
    /  \
   15   7
返回：

[3,9,20,15,7]
 

提示：

节点总数 <= 1000

思路：直接用上面的答案转化一下就行了，一行搞定。

//2个vector拼接起来
template<typename T>
vector<T> join(const vector<T>& v1, const vector<T>& v2)
{
	vector<T>ans(v1.size() + v2.size());
	copy(v1.begin(), v1.end(), ans.begin());
	copy(v2.begin(), v2.end(), ans.begin() + v1.size());
	return ans;
}
template<typename T>
vector<T> join(const vector<vector<T>> &v)
{
	vector<T>ans;
	for (auto &vi : v)ans = join(ans, vi);
	return ans;
}


class Solution {
public:
	void levelOrder3(vector<vector<TreeNode*>>&v) {
		vector<TreeNode*>v1 = *(v.end() - 1);
		vector<TreeNode*>v2;
		for (int i = 0; i < v1.size(); i++) {
			if (v1[i]->left)v2.push_back(v1[i]->left);
			if (v1[i]->right)v2.push_back(v1[i]->right);
		}
		if (v2.empty())return;
		v.push_back(v2);
		levelOrder3(v);
	}
	vector<vector<int>> levelOrder2(TreeNode* root) {
		vector<vector<TreeNode*>>v;
		vector<TreeNode*>tmp;
		vector<vector<int>>ans;
		vector<int>tmpans;
		if (!root)return ans;
		tmp.push_back(root);
		v.push_back(tmp);
		levelOrder3(v);
		for (int i = 0; i < v.size(); i++) {
			tmpans.resize(v[i].size());
			for (int j = 0; j < v[i].size(); j++)tmpans[j] = v[i][j]->val;
			ans.push_back(tmpans);
		}
		return ans;
	}
	vector<int> levelOrder(TreeNode* root) {
		return join(levelOrder2(root));
	}
};

剑指 Offer 32 - III. 从上到下打印二叉树 III

请实现一个函数按照之字形顺序打印二叉树，即第一行按照从左到右的顺序打印，第二层按照从右到左的顺序打印，第三行再按照从左到右的顺序打印，其他行以此类推。

例如:
给定二叉树: [3,9,20,null,null,15,7],

    3
   / \
  9  20
    /  \
   15   7
返回其层次遍历结果：

[
  [3],
  [20,9],
  [15,7]
]
 

提示：

节点总数 <= 1000

在剑指 Offer 32 - II. 从上到下打印二叉树 II的答案基础上，加一个翻转。


//翻转vector
template<typename T>
vector<T> frev(const vector<T>& v)
{
	vector<T> ans;
	ans.resize(v.size());
	for (int i = 0; i < v.size(); i++)ans[i] = v[v.size() - 1 - i];
	return ans;
}

class Solution {
public:
    void levelOrder(vector<vector<TreeNode*>>&v){
        vector<TreeNode*>v1=*(v.end()-1);
        vector<TreeNode*>v2;
        for(int i=0;i<v1.size();i++){
            if(v1[i]->left)v2.push_back(v1[i]->left);
            if(v1[i]->right)v2.push_back(v1[i]->right);
        }
        if(v2.empty())return;
        v.push_back(v2);
        levelOrder(v);
    }
    vector<vector<int>> levelOrder(TreeNode* root) {
        vector<vector<TreeNode*>>v;
        vector<TreeNode*>tmp;
        vector<vector<int>>ans;
        vector<int>tmpans;
        if(!root)return ans;
        tmp.push_back(root);
        v.push_back(tmp);
        levelOrder(v);
        for(int i=0;i<v.size();i++){
            tmpans.resize(v[i].size());
            for(int j=0;j<v[i].size();j++)tmpans[j]=v[i][j]->val;
            ans.push_back(tmpans);
        }
        for(int i=1;i<ans.size();i+=2)ans[i]=frev(ans[i]);
        return ans;
    }
};

力扣 1602. 找到二叉树中最近的右侧节点

给定一棵二叉树的根节点 root 和树中的一个节点 u ，返回与 u 所在层中距离最近的右侧节点，当 u 是所在层中最右侧的节点，返回 null 。

示例 1：

输入：root = [1,2,3,null,4,5,6], u = 4
输出：5
解释：节点 4 所在层中，最近的右侧节点是节点 5。
示例 2：

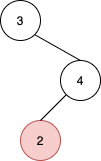
输入：root = [3,null,4,2], u = 2
输出：null
解释：2 的右侧没有节点。
示例 3：

输入：root = [1], u = 1
输出：null
示例 4：

输入：root = [3,4,2,null,null,null,1], u = 4
输出：2
 

提示:

树中节点个数的范围是 [1, 105] 。
1 <= Node.val <= 105
树中所有节点的值是唯一的。
u 是以 root 为根的二叉树的一个节点。


class Solution {
public:
    TreeNode* tar;
    int tarDeep;
    void levelOrder(vector<vector<TreeNode*>>&v, int deep){
        vector<TreeNode*>v1=*(v.end()-1);
        vector<TreeNode*>v2;
        for(int i=0;i<v1.size();i++){
            if(v1[i]==tar)tarDeep=deep;
            if(v1[i]->left)v2.push_back(v1[i]->left);
            if(v1[i]->right)v2.push_back(v1[i]->right);
        }
        if(v2.empty())return;
        v.push_back(v2);
        levelOrder(v, deep+1);
    }
    vector<vector<TreeNode*>> levelOrder(TreeNode* root) {
        vector<vector<TreeNode*>>v;
        vector<TreeNode*>tmp;
        vector<int>tmpans;
        if(!root)return v;
        tmp.push_back(root);
        v.push_back(tmp);
        levelOrder(v, 0);
        return v;
    }
    TreeNode* findNearestRightNode(TreeNode* root, TreeNode* u) {
        tar = u;
        auto v = levelOrder(root);
        cout<<tarDeep;
        cout<<v.size();
        for(int i=0;i<v[tarDeep].size();i++){
            if(v[tarDeep][i]!=u)continue;
            if(i==v[tarDeep].size()-1)return NULL;
            return v[tarDeep][i+1];
        }
        return NULL;
    }
};

本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如若转载，请注明出处：http://www.coloradmin.cn/o/185252.html

如若内容造成侵权/违法违规/事实不符，请联系多彩编程网进行投诉反馈，一经查实，立即删除！

相关文章

C++中的new、operator new与placement new

C++中的new、operator new与placement new

new operator 当我们使用了new关键字去创建一个对象时&#xff0c;你知道背后做了哪些事情吗&#xff1f; A* a new A;实际上这样简单的一行语句&#xff0c; 背后做了以下三件事情&#xff1a; 分配内存,如果类A重载了operator new&#xff0c;那么将调用A::operator new(…
阅读更多...
TencentOS安装并运行多版本php

TencentOS安装并运行多版本php

TencentOS版本3.1安装并运行php7&#xff0c;现在需要同时运行一个php8. php选择使用了php v8.0.27 采用编译安装的方式&#xff0c;编译命令如下&#xff1a; ./configure --prefix/application/php8 --with-config-file-path/application/php8/etc --with-mhash --with-o…
阅读更多...
51单片机学习笔记-4矩阵键盘

51单片机学习笔记-4矩阵键盘

4 矩阵键盘 [toc] 注&#xff1a;笔记主要参考B站江科大自化协教学视频“51单片机入门教程-2020版 程序全程纯手打 从零开始入门”。 注&#xff1a;工程及代码文件放在了本人的Github仓库。 4.1 矩阵键盘介绍 在键盘中按键数量较多时&#xff0c;为了减少I/O口的占用&#…
阅读更多...
vuex中 this.$store.dispatch() 与 this.$store.commit()

vuex中 this.$store.dispatch() 与 this.$store.commit()

一、理解 this.$store.dispatch 分发 actions-> 调用 mutations->改变 states 二、思考 1、为什么不直接分发 mutation mutation 有必须同步执行的限制&#xff0c;而 Action 不受约束&#xff0c;可以在 action 内部执行异步操作2、Action 通常是异步的&#xff0c;…
阅读更多...
配置日志输出到指定位置的文件，单独报错error级别以上的日志，按日志类别打印日志

配置日志输出到指定位置的文件，单独报错error级别以上的日志，按日志类别打印日志

目录1.配置文件2.测试程序&#xff1a;工具&#xff1a;log4j的jar包、配置文件log4j.properties(文件名自定义)、eclipse或IDEA 更多参考&#xff1a;https://www.cnblogs.com/ITtangtang/p/3926665.html、 1.配置文件 新建一个配置文件log4j.properties&#xff08;我把它放…
阅读更多...
区块链游戏走出一地鸡毛，元宇宙3D国风链游或成最大受益者

区块链游戏走出一地鸡毛，元宇宙3D国风链游或成最大受益者

曾推出过《Cytus》《Deemo》《聚爆》等知名游戏的雷亚&#xff0c;其CEO游名扬在接受采访时曾谈到&#xff0c;游戏产业是文化产业加上科技产业的组合体&#xff0c;这两者是组成游戏产业的主要部分。看游戏的趋势&#xff0c;就要针对文化和科技的趋势上来看。 这话没错。 20…
阅读更多...
flutter StreamController，ValueListenableBuilder，NotificationListener

flutter StreamController，ValueListenableBuilder，NotificationListener

FutureBuilder &#xff08;异步数据更新&#xff09; StreamBuilder &#xff08;异步数据更新&#xff09; 构造函数 特点 接收多个异步操作的结果class StreamBuilder<T> extends StreamBuilderBase<T, AsyncSnapshot<T>>{}单订阅&#xff1a;StreamCo…
阅读更多...
在Linux中进行Hbase搭建

在Linux中进行Hbase搭建

在公网IP为x.x.x.x、y.y.y.y和z.z.z.z并装有Centos8的服务器上进行hadoop集群搭建、zookeeper集群搭建和hbase搭建&#xff0c;都安装hadoop-3.1.3、server-jre-8u202-linux-x64、apache-zookeeper-3.6.4-bin和hbase-2.5.0-bin。 环境准备&#xff08;三台服务器都一样&#x…
阅读更多...
基于javaweb宠物领养平台管理系统设计和实现

基于javaweb宠物领养平台管理系统设计和实现

基于javaweb宠物领养平台管理系统设计和实现 博主介绍&#xff1a;5年java开发经验&#xff0c;专注Java开发、定制、远程、文档编写指导等,csdn特邀作者、专注于Java技术领域 作者主页 超级帅帅吴 Java毕设项目精品实战案例《500套》 欢迎点赞 收藏 ⭐留言 文末获取源码联系方…
阅读更多...
C++基础——C++ 判断

C++基础——C++ 判断

C基础——C 判断C 判断判断语句C if 语句语法流程图? : 运算符C 判断 判断结构要求程序员指定一个或多个要评估或测试的条件&#xff0c;以及条件为真时要执行的语句&#xff08;必需的&#xff09;和条件为假时要执行的语句&#xff08;可选的&#xff09;。 下面是大多数编…
阅读更多...
DAMA数据管理知识体系指南之数据管理概述

DAMA数据管理知识体系指南之数据管理概述

第2章 数据管理 2.1 引言 2.2 使命和目标 使命 在信息的可用性、安全性和质量方面&#xff0c;满足并超越企业中所有利益相关者的信息要求。 战略目标 &#xff08;1&#xff09;理解企业和所有利益相关者的信息需求。 &#xff08;2&#xff09;获取、存储、保护和确保数据资…
阅读更多...
堆的结构及函数接口、堆排序，TopK

堆的结构及函数接口、堆排序，TopK

本篇内容涉及到二叉树的概念及性质&#xff0c;可参考文章 树和二叉树的概念及性质 文章目录一、堆的概念二、堆的存储结构三、堆的函数接口1. 初始化及销毁2. 打印函数3. 堆的插入4. 堆的删除5. 取堆顶、判空、数据个数四、建堆算法和时间复杂度1. 向上调整建堆2. 向下调整建堆…
阅读更多...
CTFshow--web--红包题第二弹

CTFshow--web--红包题第二弹

查看源代码&#xff0c;按注释提示&#xff0c;构造参数试试?cmdaa<?php #error_reporting(0); ?> <html lang"zh-CN"><head><meta http-equiv"Content-Type" content"text/html; charsetUTF-8" /><meta name&quo…
阅读更多...
MATLAB绘制爱心曲线并导出

MATLAB绘制爱心曲线并导出

MATLAB绘制爱心曲线并导出 爱心曲线的表达式&#xff1a; f(x)x2/3e3(π−x2)1/2sin(aπx)f(x)x^{2/3}\frac e 3(\pi-x^2)^{1/2}sin(a\pi x) f(x)x2/33e​(π−x2)1/2sin(aπx) f (x,a)x.^2.^(1/3)exp(1)/3*(pi-x.^2).^(1/2).*sin(a*pi*x); h figure(color,[1 1 1]); set(g…
阅读更多...
应用系统与钉钉集成案例及操作步骤

应用系统与钉钉集成案例及操作步骤

1、准备钉钉应用 1.1、注册钉钉账号 作为钉钉的企业管理员&#xff0c;首先登录钉钉官网&#xff0c;注册一个钉钉账号。 如果已经有账号&#xff0c;则直接使用即可。 钉钉官网&#xff1a;https://www.dingtalk.com/ 1.2、开通企业团队 企业管理员使用账号登录钉钉。 如…
阅读更多...
如何限制docker容器使用内存大小

如何限制docker容器使用内存大小

本文介绍如何通过docker运行参数配置限制docker容器可以使用的内存上限。docker容器默认可以使用全部宿主机的所有内存和 swap 分区&#xff0c;比如宿主机的内存是32G&#xff0c;则运行一个docker容器最多可以分配到32G内存&#xff0c;如果启用了多个docker容器&#xff0c;…
阅读更多...
CSS实现文本显示两行

CSS实现文本显示两行

效果图 text-overflow: ellipsis;display: -webkit-box;-webkit-line-clamp: 2;-webkit-box-orient: vertical;display: -moz-box;-moz-line-clamp: 2;-moz-box-orient: vertical;overflow-wrap: break-word;word-break: break-all;white-space: normal;overflow: hidden;text-…
阅读更多...
SAP ADM100-2.2 SAP系统开启过程中的配置文件

SAP ADM100-2.2 SAP系统开启过程中的配置文件

SAP系统的每个实例需要的数据都在文件系统中，包括所有实例都需要访问的全局数据（Globally）和个别实例需要访问的数据。在文件系统汇总，实例需要的数据被包含在usr/sap目录，在这里被进一步组织到子目录。 【注意】：业务数据和相关数据被存储在数据库中，数据库根据不同的制…
阅读更多...
【GD32F427开发板试用】三、USB转CAN功能开发与试用总结

【GD32F427开发板试用】三、USB转CAN功能开发与试用总结

本篇文章来自极术社区与兆易创新组织的GD32F427开发板评测活动&#xff0c;更多开发板试用活动请关注极术社区网站。作者&#xff1a;chenjie 【GD32F427开发板试用】一、环境搭建与freertos移植 【GD32F427开发板试用】二、USB库移植与双USB CDC-ACM功能开发 【GD32F427开发板…
阅读更多...
【C++】IO流

【C++】IO流

​&#x1f320; 作者&#xff1a;阿亮joy. &#x1f386;专栏&#xff1a;《吃透西嘎嘎》 &#x1f387; 座右铭&#xff1a;每个优秀的人都有一段沉默的时光&#xff0c;那段时光是付出了很多努力却得不到结果的日子&#xff0c;我们把它叫做扎根 目录&#x1f449;C语言的输…
阅读更多...
推荐文章
最新文章

Copyright @ 2022~2023