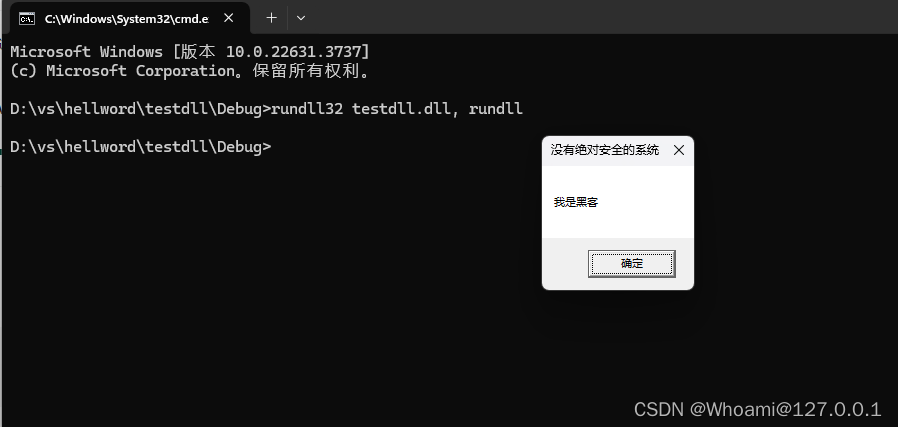
洛谷P3366 -【模板】最小生成树
题目描述
如题,给出一个无向图,求出最小生成树,如果该图不连通,则输出 orz。
输入格式
第一行包含两个整数 N , M N,M N,M,表示该图共有 N N N 个结点和 M M M 条无向边。
接下来 M M M 行每行包含三个整数 X i , Y i , Z i X_i,Y_i,Z_i Xi,Yi,Zi,表示有一条长度为 Z i Z_i Zi 的无向边连接结点 X i , Y i X_i,Y_i Xi,Yi。
输出格式
如果该图连通,则输出一个整数表示最小生成树的各边的长度之和。如果该图不连通则输出 orz。
样例 #1
样例输入 #1
4 5
1 2 2
1 3 2
1 4 3
2 3 4
3 4 3
样例输出 #1
7
提示
数据规模:
对于 20 % 20\% 20% 的数据, N ≤ 5 N\le 5 N≤5, M ≤ 20 M\le 20 M≤20。
对于 40 % 40\% 40% 的数据, N ≤ 50 N\le 50 N≤50, M ≤ 2500 M\le 2500 M≤2500。
对于 70 % 70\% 70% 的数据, N ≤ 500 N\le 500 N≤500, M ≤ 1 0 4 M\le 10^4 M≤104。
对于 100 % 100\% 100% 的数据: 1 ≤ N ≤ 5000 1\le N\le 5000 1≤N≤5000, 1 ≤ M ≤ 2 × 1 0 5 1\le M\le 2\times 10^5 1≤M≤2×105, 1 ≤ Z i ≤ 1 0 4 1\le Z_i \le 10^4 1≤Zi≤104。
样例解释:
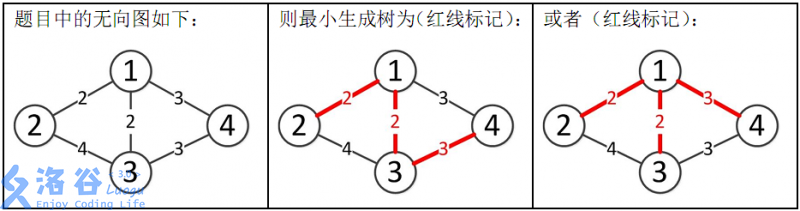
所以最小生成树的总边权为 2 + 2 + 3 = 7 2+2+3=7 2+2+3=7。
前置知识:并查集,最小生成树
这道模板题非常简单,给定一个无向图的各条边以及权值,求最小生成树。可以采用
P
r
i
m
Prim
Prim算法或者
K
r
u
s
k
a
l
Kruskal
Kruskal算法。我用的是
K
r
u
s
k
a
l
Kruskal
Kruskal,因为写起来简单(
基本思路如下:
- 先读入点数 n n n和边数 m m m,然后用一个结构体数组存放每一条边及其权值,用一个 i n t int int变量 a n s ans ans存放该最小生成树各边的长度之和。
- 对该结构体使用 C + + C++ C++自带的 S T L STL STL库中的 s o r t ( ) sort() sort()函数,对其进行权值的从小到大的排序。
- 然后,从权值最小的边开始遍历所有的边,若该边连接的两个顶点不在一个集合内,则使用并查集进行合并,并在 a n s ans ans中加上该边的权值。
- 最后,再对所有点进行一次遍历,判断是否都在一个集合内以确定该图是否连通。若不连通,输出
orz;若连通,则输出 a n s ans ans。
以下是100pts的代码:
#define _CRT_SECURE_NO_WARNINGS 1
#include<cstdio>
#include<cstdlib>
#include<cstring>
#include<iostream>
#include<algorithm>
using namespace std;
const int MAXN = 5007;//最大点数
const int MAXM = 200007;//最大边数
int n, m;
int f[MAXN];//并查集
struct Node {
int x, y, z;
}Arc[MAXM];//边集数组
inline int Find(int x) {//并查集寻根&路径压缩
return x == f[x] ? x : f[x] = Find(f[x]);
}
inline void Merge(int x, int y) {//并查集的合并操作
int rx = Find(x), ry = Find(y);
if (rx == ry)return;
else f[ry] = rx;
return;
}
inline bool cmp(Node u, Node v) {//结构体排序规则
return u.z < v.z;
}
inline bool Judge() {//判断所有点是否处于同一集合
int Root = Find(1);
for (int i = 2; i <= n; ++i)
if (Find(i) != Root)return false;
return true;
}
int main() {
cin >> n >> m;
for (int i = 1; i <= n; ++i)f[i] = i;//并查集初始化
for (int i = 1; i <= m; ++i)
cin >> Arc[i].x >> Arc[i].y >> Arc[i].z;
sort(Arc + 1, Arc + 1 + m, cmp);//结构体排序,需要的头文件是#include<algorithm>
int ans = 0;//存放最小生成树各边的长度之和,int够用
for (int i = 1; i <= m; ++i) {//遍历所有边
if (Find(Arc[i].x) != Find(Arc[i].y)) {//若顶点x和顶点y不在同一集合
Merge(Arc[i].x, Arc[i].y);//合并
ans += Arc[i].z;//加上边的权值
}
}
if (!Judge())cout << "orz" << endl;//若图不连通
else cout << ans << endl;
return 0;
}
完整代码也可以到我的Github查看:传送门
总之就是个非常简单的板子题,适合用来练手。
以上。